低功率风力涡轮机叶片设计优化

低功率失速调节型风力涡轮机的增强设计方法论。动量‐叶素理论与动参考系‐雷诺平均纳维‐斯托克斯方程（MRF‐RANS）结合及其与现有设计的对比

A B S T R A C T

风能的重要性在过去几十年中不断增加。安装在城市附近的小微型风力涡轮机的能量产生经历了显著增长。本研究致力于开发一种适用于各种风况的低功率叶片设计方法论。

首先，将使用低计算成本工具叶素动量理论（BEMT）进行完整的实验设计，以排除那些明显不符合系统要求的设计方案。随后，对剩余的设计方案采用计算流体力学（CFD）方法论进行分析，以考虑三维效应的影响。

研究发现，无量纲功率曲线的左侧斜率值是设计中的一个关键参数。

该方法论已通过来自NREL第六阶段风力涡轮机的实验结果进行了验证，从而得出结论：动量‐叶素理论能够提供初步设计的准确结果，但这些结果仍需通过计算流体力学进行修正。

对提出的设计结果进行了分析，并与一款商用现有叶片的CFD预测结果进行了比较，该商用叶片的设计旨在满足类似的工作条件。对于提出的设计，预测表明其在最大功率和可控性方面表现更优。

1. 引言

由于全球变暖可能导致严重的气候变化，人们对可再生能源的开发产生了新的积极兴趣。特别是，在过去二十年中，风力涡轮机发电所占的比例持续增加（雅各布森和德吕奇，2011年），自20世纪90年代以来，年均增长率达到28%。预计到2020年代，风能将产生约1200吉瓦的电力，占总能源生产的12%。在此背景下，预计总装机容量的大约3%将进入国内市场（施雷克，2008年）。

在风力涡轮机开发过程中，最需要关注的关键特性之一是叶片。接下来是为发电机和齿轮箱开发控制系统。因此，在新设计开发过程中，优化叶片形状和风力发电场的位置至关重要（穆切等人，2016年）。

这一较大比例使得小型风力涡轮机（SWT）在低最大功率输出（根据 IEC 61400-2,2006，不超过50kW）方面变得尤为引人关注。通常，小型风力涡轮机不具备变桨调节功能，无法在不同工作条件下优化攻角，因此有必要在广泛的风速和转速范围内进行被动优化。

由于这类风力涡轮机本质上是批量生产的，因此即使在设计过程的早期阶段，改进风力涡轮机叶片几何形状也变得非常重要。尽管文献中已提出一些有趣的优化方案（参见Roshan 等人 (2015)），但其应用成本较高，因此值得研究更简单的改进方法。

在设计阶段，从成本降低的角度来看，风力涡轮机性能的预测是值得关注的。在此背景下，通常使用计算成本较低的工具。其中，叶素动量理论（BEMT）已被广泛用于研究叶片几何形状在设计条件和非设计工况下的表现（例如参见Lee 等人 (2016) 或 Benini 和 Toffolo (2002)）。

动量‐叶素理论的主要假设是，风力涡轮机每个翼型截面处的flow 可被视为近似二维流动。二维假设无法预测失速延迟现象，可能导致在接近失速后工作点时对发电功率的低估（Rooij和Arens，2007）。尽管已有一些模型被开发出来用于考虑这一效应（杜和塞利格，1998），但本文将在后续阶段考虑任何三维问题。

动量‐叶素理论可用于定义在风力涡轮机设计点处最大化输出功率的几何结构（曼维尔等，2009）。然而，由于风力涡轮机在多种非设计工况下也需要良好运行，仅以最大化设计功率为准则已不再适用。本文探索并应用BEMT方法，以选择一种能够在广泛运行条件下满足功率与控制要求的构型。

当使用BEMT方法获得设计时，需要对预测性能进行修正，以考虑可能重要的三维效应（莫和李，2012）。通常采用不同复杂程度的计算流体力学（CFD）来实现这一目标。例如，Tran 和 Kim (2016) 对处于纵荡运动下的完整风力涡轮机进行了非定常雷诺平均纳维‐斯托克斯（URANS）计算，发现塔架的影响与平均发电功率相比相对较小。类似的结论也可从Mo 等人 (2013)的研究中得出，他们采用大涡模拟（LES）研究了完整的NREL第六阶段风力涡轮机。因此，采用动参考系中的稳态计算方法可能会显著减少计算时间。

需要注意的是，当预测风力涡轮机阵列的行为时，上述假设仅部分成立，这一点可从Kang et al.(2014)或Santoniet al.(2017)的研究中推断得出。然而还应注意，在处理低功率风力涡轮机时，它们通常以独立配置安装，并且由于其特征长度较小，尾流产生显著影响的距离也会更短。

文献中也可找到一些研究，其中考虑了叶片的弹性变形。例如，Pour-rajabian et al.(2016)计算了作用在叶片上的fl弯曲载荷，发现其与风力涡轮机尺寸相比很小。类似的结果也可在Ponta et al.(2016)中找到。

关于此类flow的实验验证，美国国家可再生能源实验室（NREL）提供了大量信息。已发表文献中的大量研究基于计算结果与实测数据的验证和比较（（汉德等，2001），（西姆斯等，2001））。例如，伊斯法哈尼安等人（2013）对NREL第二阶段风力涡轮机进行了CFD与BEMT计算，表明了这两种方法的适用性。对于NREL Phase VI，Yelmule和Eswara Rao(2013) 也得出了类似的结论。

本文提出了一种改进的叶片设计方法论，该方法论不仅能够定义在最佳条件下实现最大输出功率的设计，还引入了额外的要求以考虑可控性问题。该设计方法论首先通过动量‐叶素理论（BEMT）对可能的叶片几何形状进行初步广泛筛选排除，然后通过雷诺平均纳维‐斯托克斯（RANS）研究，从少量设计方案中剔除不合适的情况，具体将在后文说明。

在本研究中，采用了一种经典的动量‐叶素理论方法论来获得小半径风力涡轮机的改进设计。然而，BEMT模型包含了一些可能导致结果不准确的假设，尤其是在存在显著流动分离以及三维效应变得重要的情况下。因此，必须使用能够考虑这些效应的计算工具（如计算流体力学）对最终的设计进行研究。该过程的主要目标是：（a）开展实验设计（DOE），以生成不仅在能量最大可能产出方面最优，而且在超出设计工况的工作条件下表现出可接受性能的几何结构（主要是通过改进的可控性使叶片具备承受高风速的能力）。为此，使用动量‐叶素理论来获取实验设计过程中生成的所有几何结构的特征，并剔除那些行为表现不可接受的设计。由于前述该理论存在的局限性，未被剔除的叶片族必须随后采用三维方法（如雷诺平均纳维‐斯托克斯方程（RANS））进行进一步研究，以确保其仍满足要求，并剔除不符合要求的设计。

本工作的第二个目标是（b）将所得到的设计与具有相似特性的其他商用风力涡轮机在最大功率输出和可控性方面进行比较。

关于在高风速环境下进行能够承受的风力涡轮机设计的必要性，已知对于失速调节型水平轴风力涡轮机（HAWT），必须考虑当风速超过临界值时可能出现的电路烧毁或结构失效风险（耶尔穆莱和埃斯瓦拉饶，2013），（陈和夏，2016））。在此背景下，本文将展示如何利用叶片的无量纲功率曲线的斜率作为一个关键设计参数，在文献中尚未得到充分探讨，以获得能够在宽风速范围内发电并避免该风险的设计。

为了评估这一目标，工作流程必须按照图1所示进行组织。本文结构可分为三个主要部分：首先，需要建立并验证计算流体力学（CFD）和动量‐叶素理论（BEMT）的方法论。这将在第2和3节中完成，其中将利用NREL Phase VI的可用实验数据进行验证。

一旦该方法论被证实能够提供良好的结果，将设计并使用动量‐叶素理论（BEMT）进行一系列计算，由于其较低的计算成本，可对一组完整的候选几何结构的行为提供较好的初步近似。此阶段的第二步是选择一个较小的候选几何结构家族，并利用计算流体力学（CFD）对其进行分析，以修正动量‐叶素理论（BEMT）的结果，考虑三维效应，并剔除在这些计算完成后表现不佳的设计。该工作阶段见第3.1节，仅展示了最终叶片的选择及其与CFD的对比。关于本节中使用雷诺平均纳维‐斯托克斯方程（RANS）排除其他叶片的情况，读者可参考第4.2节末尾。

最后，一旦提出最终设计，就有必要将其与其他现有解决方案进行比较，以检验其商业适用性。在本文中，所提出的设计与一款领先的低功率风力涡轮机——商用叶片Skystream进行了对比。由于该设计具有弯曲叶片的特点，三维效应将显著影响其性能，因此仅通过计算流体力学（CFD）方法对其进行分析。此外，还将分析和讨论其他气动部件的添加，例如涡流发生器（VG）。该阶段在第4.2节中展开，读者还将在该节中找到关于商用叶片、提出的设计以及一种替代几何结构的可控性的详细讨论。该替代几何结构在动量‐叶素理论（BEMT）方法论下是有效的，但在进行雷诺平均纳维‐斯托克斯方程（RANS）修正后，发现其在控制方面表现不佳，因此被舍弃。

2. 理论背景

2.1. 动量叶素理论

本文采用动量‐叶素理论来预测一组可能的叶片设计的稳态特性，因其具有低计算成本。BEMT模型在文献中已被广泛使用和验证，可用于进行相对较快且准确的预测（马德森等人，2010）。

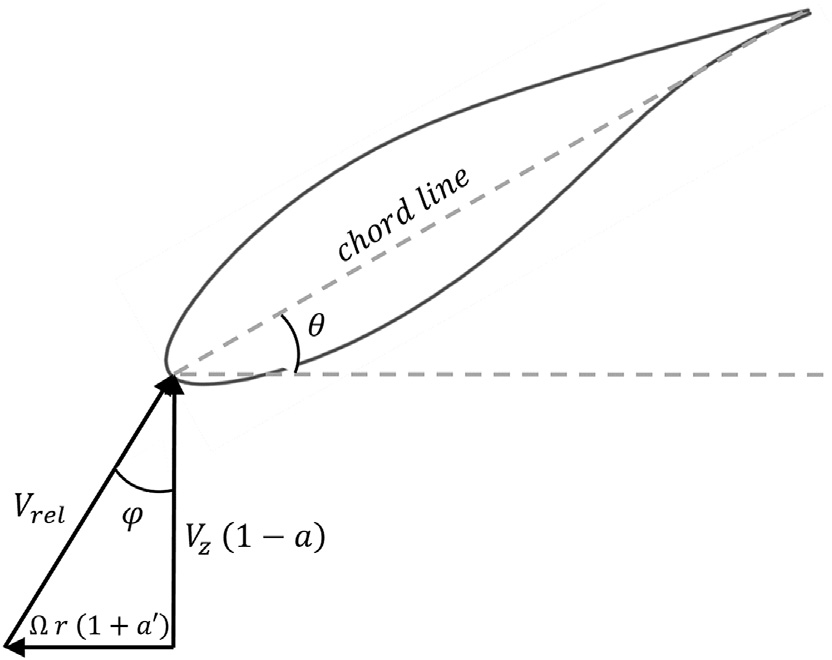
当流动被视为近似二维时，可在距离为 r处、具有桨距角 θ和弦长 c的 Hansen 等人，2006所述叶片翼型上建立速度图，如图2所示：

这里，Vz是风速， Ω是风力涡轮机转速，而a ¼ vi=Vz和a’ ¼ ω’=Ω分别是轴向和切向诱导速度。Vrel是相对风速的大小，其显示一个相对角度 φ。这些值可用于计算攻角以及翼型对法向力FN和功率P的贡献，如下所示（曼维尔等，2009）：

$$
\tan\varphi = \frac{V_z(1 - a)}{\Omega r(1 + a’)} \
\alpha = \varphi - \theta \
F_N = \frac{B}{2} \rho V_{\text{rel}}^2 (C_l \cos\varphi + C_d \sin\varphi) c \, dr \
dP = \frac{B \Omega}{2} V_{\text{rel}}^2 (C_l \sin\varphi - C_d \cos\varphi) c r \, dr
$$

其中 B为构成风力涡轮机转子的叶片数，Cl和 Cd分别为翼型的升力和阻力系数。这些系数是攻角的函数，可通过测量（Somers，1997）或计算研究（Esfahanian et al.，2013）获得。

一旦已知诱导项 a 和 a’ 的值，总力和功率便可立即推导出：

$$
F_N = \int_0^R dF_N, \quad P = \int_0^R dP
$$

诱导因子可通过迭代方法获得。其中一种最常用的方法是从动量方程的微分圆周（宽度为 dr）出发，引入无量纲叶尖速比 λ ¼ (ΩR)/Vz，可得（Manwell et al., 2009）：

$$
dC_T =
\begin{cases}
8Fa(1 - a)x \, dx & \text{if } a \leq \frac{2}{5} - \frac{4}{9}x \
[4 + a(20 - 18F) - a^2(25 - 18F)] \, dx & \text{if } a > \frac{2}{5}
\end{cases}
$$

$$
dC_P = 8Fx^3\lambda^2a’(1 - a) \, dx
$$

此处，CT ¼ 2FN/(ρπR²Vz²)、CP ¼ 2P/(ρπR²Vz³)以及 x ¼ r/R 分别为无量纲法向力、功率和位置。系数 F 用于考虑叶尖处的损失，确定该系数最常用的近似方法之一是基于普朗特方法（见 Vries (de Vries, 1979)）：

$$
F = \frac{2}{\pi} \cos^{-1} \left[ \exp \left( -\frac{B(1 - x)}{2x \sin\varphi} \right) \right]
$$

一旦获得叶片各段的诱导项并对方程 (2)进行积分，即可得到风力涡轮机的功率和力系数。所用方程的无量纲形式有一个重要优点：对于给定的桨距和涡轮机几何结构，它们仅是 λ和雷诺数（Hau, 2013）的函数。

2.2. 雷诺平均纳维‐斯托克斯方程

本文中，通过在旋转参考系上建立的雷诺平均纳维‐斯托克斯（RANS）方程对最优叶片形状周围的流体流动进行建模。这些方程可从完整的质量、动量和能量守恒方程组推导而来，并在下文中针对不可压缩流动给出（Pope, 2009）。

$$
\begin{cases}
\frac{\partial U_i}{\partial x_i} = 0 \
\frac{\partial U_i}{\partial t} + U_j \frac{\partial U_i}{\partial x_j} = \nu \frac{\partial^2 U_i}{\partial x_j \partial x_i} - \frac{\partial \overline{u_i u_j}}{\partial x_j} - \frac{1}{\rho} \frac{\partial p}{\partial x_i} + f_i
\end{cases}
$$

其中 Ui表示平均速度 ith方向上的分量 field，U!；ρ和 ν分别为流体的密度和运动粘度；fluid，分别；p表示平均压力 field，而 fi表示作用在流体上的惯性力和体积力在 ith方向上的分量。当方程在旋转坐标系中建立时，这些项可按如下方式计算（Batchelor，1967）：

$$
\vec{f} =
\begin{pmatrix}
f_x \ f_y \ f_z
\end{pmatrix}
= -\frac{d\vec{\omega}}{dt} \times \vec{r} + \vec{\omega} \times (\vec{\omega} \times \vec{r})
$$

其中 !ω表示参考系的转速，!r是流体中某一点的位置矢量。

方程(5)的闭合只能通过模拟 $\overline{u_i u_j}$ 项来实现，这些项通常被称为雷诺应力。选择合适的湍流模型对于评估流动特性至关重要。本文将采用 k− ω模型结合剪切应力输运（SST）来实现这一目的。该湍流模型在文献中已广泛用于此类流动，并表现出可接受的性能。例如，Mosh-fegui 等（2012）使用该模型对 NREL Phase VI 风力涡轮机在不同近壁网格分辨率下的流动进行了计算，获得与实验数据相比合理良好的结果（汉德等，2001）‐（西姆斯等，2001）。使用相同的湍流模型，Yelmule 和 Eswara Rao（2013）也获得了类似的结果。

梅恩特（1986）k− ω提出了一种SST模型，该模型是一种过渡模型，其公式在靠近壁面处采用威尔考克斯（1986）提出的k湍流模型，在远离壁面区域则采用k− ε模型，从而解决了这两种模型的主要缺陷。此外，该模型还包含一个关于湍流动能的输运方程

能量k，k− ε和k− ω湍流模型分别求解湍流耗散率ε和比湍流耗散率ω的输运方程。这些变量通过 ω∝ε/k相关联，并可用于获得湍流粘度 νt ¼ Cμ k²/ε（其中Cμ ¼ 0:09为一个模型常数）。该湍流粘度用于模拟雷诺应力张量的值：

$$
\overline{u_i u_j} = \frac{2}{3} k \delta_{ij} - \nu_T \left( \frac{\partial \langle U_i \rangle}{\partial x_j} + \frac{\partial \langle U_j \rangle}{\partial x_i} \right)
$$

3. 方法论

3.1. 实验设计

在本节中，提出并通过动量‐叶素理论分析了一种弦长和扭角的几何分布。大量研究致力于在给定工作条件下获得最优的最大功率系数。对于例如，伯德特和范特伦（2012）假设雷诺数会影响二维翼型特性，针对给定叶尖速比找到了一种优化解。结果表明，这种影响实际上几乎可以忽略不计。

对于给定的设计值 αd和 λd，斯佩拉（2009）证明了对叶片单元的功率系数进行优化等价于求函数 f(a；a’)的定义：

$$
f(a, a’) = a’(1 - a)
$$

约束条件为：

$$
(\lambda_d x)^2 \frac{a’}{1 + a’} = a(1 - a)
$$

一旦方程（8）和（9）被求解，对于已知的翼型截面，其中 Cl(αd) ≫ Cd(αd)，其几何参数可按如下方式计算：

$$
\sigma(x) = \frac{4a’(1 + a’) \sin^2 \varphi}{\cos \varphi x C_l(\alpha_d)} \
\theta(x) = \varphi - \alpha_d
$$

其中 σ(x) ¼ Bc(x)/(2πR) 定义为位于距轮毂无量纲距离 x 处翼型的局部实度。

通常，αd 的取值应使每个翼型截面在设计叶尖速比 λd 下具有最大气动效率 Cl/Cd。该近似方法也可获得功率系数的最大局部值，但可能导致非设计工况点性能不可接受。

由于低功率风力机的成本性能要求，有必要尽量减少自动控制的需求。因此，为了确保在高风速下自动控制无需施加不可接受的制动转矩，风力机必须有效实现失速调节。由于发电功率按 P∝CP Vz³ 的比例变化，失速调节涡轮机的必要性导致在最大预期风速下满足条件 dP/dVz < 0。

该条件可仅用叶尖速比和功率系数表示为：

$$
\frac{dC_P}{d\lambda} > 3C_P
$$

方程 (11)表明，为了确保在最大风速下的可控性，CP − λ曲线从左侧起必须具有较高的斜率。

为了确保风力涡轮机易于控制，同时其最大功率系数也较高，采用 αd作为最大Cl/Cd的判据并不足够准确。因此，通过改变λd和 αd并应用公式(10)，定义了一组实验设计（DOE）。随后，为每种可能的设计获得了无量纲功率曲线。从中选择最优叶片，以满足公式(11)的要求，并考虑叶片应具有结构上可行性。实验设计（DOE）中所考虑的参数范围及步长如下：

$$
\lambda_d \in [4.5, 10.5], \Delta\lambda = 1 \
\alpha_d \in [3, 12]^\circ, \Delta\alpha = 1^\circ
$$

选择了NREL S809翼型，因为它已被广泛研究，并显示出良好的性能（He和Agarwal，2014）。此外，该翼型在广泛的攻角范围内具有大量可用数据（Somers，1997）。该翼型将用于风力涡轮机的整个叶片半径R。在小型风力涡轮机设计中，采用单一翼型是一种常见做法（（Singh和Ahmed，2013），（Tum-mala等，2016））。由于此类风力涡轮机尺寸较小，其所有截面均可视为在低雷诺数范围内工作，因此在根部和叶尖使用不同翼型对风力涡轮机性能的提升极为有限。

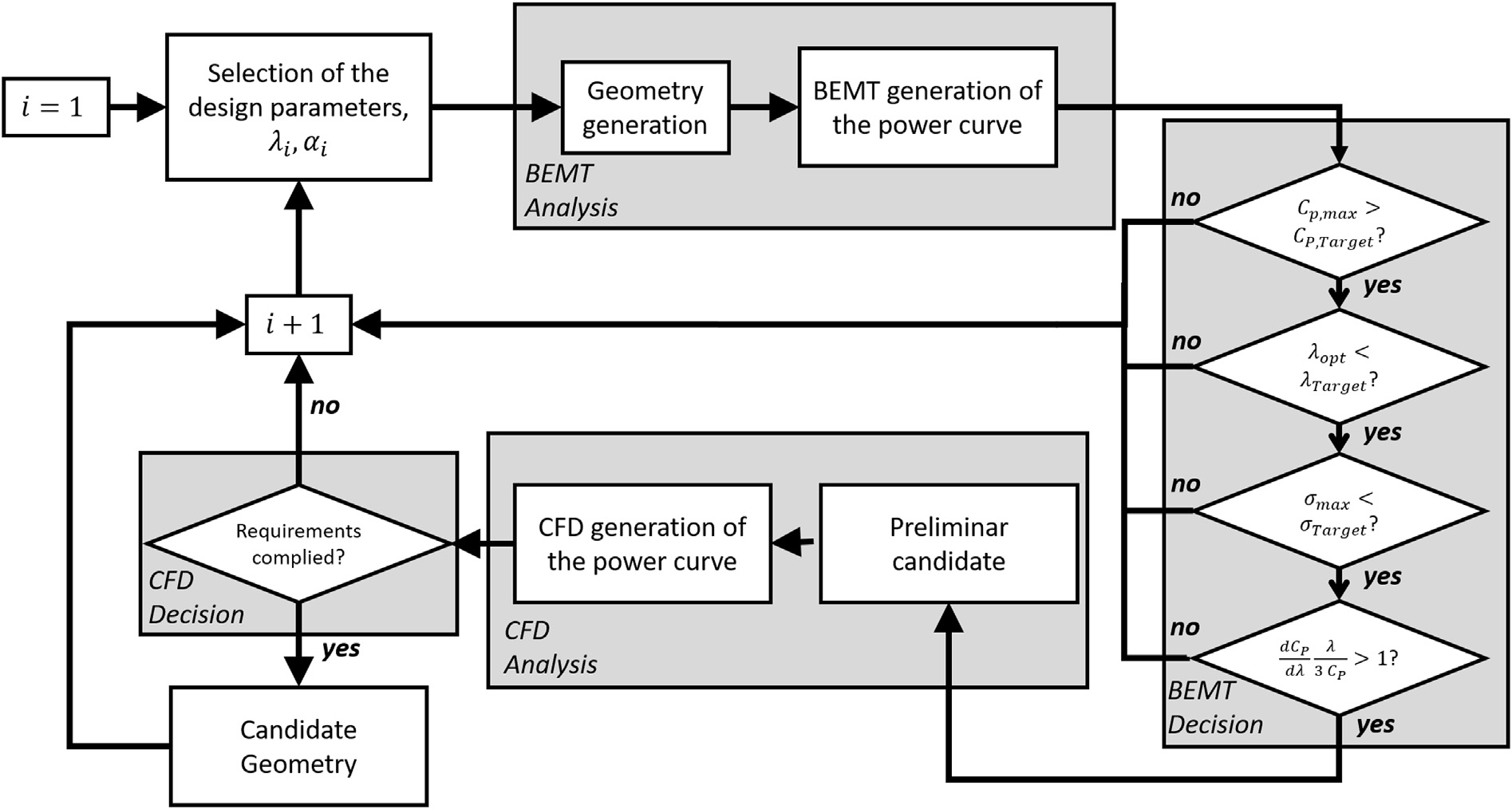
在介绍完DOE方法后，将生成一组完整的候选几何结构。随后必须进行决策过程，如图3所示。在选定λdesign和 αdesign之后，将生成一个可能的几何结构，并使用动量‐叶素理论进行分析。如果动量‐叶素理论计算的设计满足某些特定要求（稍后将详细说明），则该设计将被视为初步候选，并进一步使用计算流体力学进行分析。如果仍然满足类似的限制条件，则该几何结构将被视为最终候选。如果在任何阶段有任何要求未被满足，则该叶片几何结构将被舍弃。

传统上，选择主要基于构造性和最大功率准则。然而，在设计失速调节型风力涡轮机时，必须考虑到叶片应易于控制，以满足左侧斜率条件，即公式(11)。需要注意的是，根据当前的方法论，并取决于参数扫描的执行方式，可能会有多个设计方案进入最终候选阶段。如果出现这种情况，所有得到的候选方案均为有效设计，且可对其施加额外条件（例如，可选择具有更高最大功率系数的设计）。在本研究的条件下，经过计算流体力学决策阶段后，仅有一种几何结构满足要求。

在定性描述实验设计后，需要确定将考虑各个参数的具体取值。这些参数总结如下：

• 新型叶片设计的最大功率系数必须较高。在此意义上，认为所得到的叶片在最佳条件下应提供的最大功率系数为(CP)optim > 0.37，这对应于叶片半径R ¼ 2.50 m、风速Vz ¼ 7m s⁻¹时的发电功率约为P ¼ 1500 W。
• 为了在设计条件下最小化辐射噪声，最佳转速应尽可能低。因此，假设一个可接受的设计应在λoptim < 6.5时达到其最大功率系数，这对应于前一点所述条件下约Ω ¼ 170 rpm的最佳转速。将显示，RANS预测预计会对此参数提供更高的估计值。因此，在CFD评估期间，由于可控性限制更为重要，该约束将略有放宽。请注意，即使对该参数进行了上述放宽，RANS预测的运行转速仍将保持在一定范围内。
• 如前所述，为了获得易于控制的失速调节叶片风力涡轮机的几何结构，功率曲线的左侧斜率应尽可能高。当前设计的目的是说明新型风力涡轮机在 λ ¼ 0.85·λoptim时应符合

$$
\frac{dC_P}{d\lambda} \lambda - 3 C_P > 1
$$

• 在叶尖速比较低的情况下，风力涡轮机的性能应保持可接受，以确保正常启动。注意，这是一条定性描述。由于在 λ取值较低时，动量‐叶素理论（BEMT）假设的适用性仅部分成立，因此有可能观察到某些基于BEMT预测的设计在特定条件下出现功率系数为负的情况。这显然不会真实发生，但可以认为，即使考虑了所采用的简化假设，该设计在低转速下的性能仍不可接受。
• 风力机叶片的制造应尽可能简单。从这个意义上说，最大局部实度σ（如将看到的，其位置靠近轮毂）不应超过某一特定值。如果该实度过高，则在它与轮毂之间构建过渡部分将变得困难。因此，在本研究中，假设设计应满足σmax < 0.10。

所有符合前述约束条件的叶片几何形状将被视为可能的候选方案（五个候选方案，针对前述约束条件）。这些方案将通过CFD进行研究，以考虑三维效应，并确保所研究的设计满足规定的要求，排除不符合要求的方案。尽管这对所有适用于动量‐叶素理论的叶片都进行了，但出于简洁性考虑，仅在第四.1节展示最终选择的结果。同时请注意，第二个要求将略有放宽。

3.2. CFD建模

为了考虑流动的三维效应，采用通用商业软件STAR CCM+，基于有限体积法，在动参考系（MRF）中对公式(5)进行数值求解，并采用二阶迎风离散化。为了设置CFD计算，首先对NREL Phase VI转子进行了分析，并与现有的实验测量结果进行了验证（见第三.3节）。该风力涡轮机由2个叶片组成，半径为R ¼5.11m。该风力涡轮机的弦长和扭角分布在文献中可以找到（（汉德等，2001））。

由于对于任何运行条件，M ≪ 0.3，流动可被视为不可压缩。此外，守恒方程在随叶片角速度运动的动参考系中建立， Ω。在此类参考系中建立方程可以忽略瞬态效应，仅求解定常平均流动。这一假设是合理的，文献中已有相关观察。例如，Li 等人 (2012) 针对 NREL Phase VI 采用了分离涡模拟（DES）进行动态模拟。该文献表明，在优化过程中，采用定常解的假设是合适的。

其他需要进行的简化是周期性假设。因此，仅对单个叶片进行建模，从而可以使用角度为Δθ ¼ 2π/叶片数的缩小的计算域。该假设已在文献中成功应用（Lee 等，2012）。

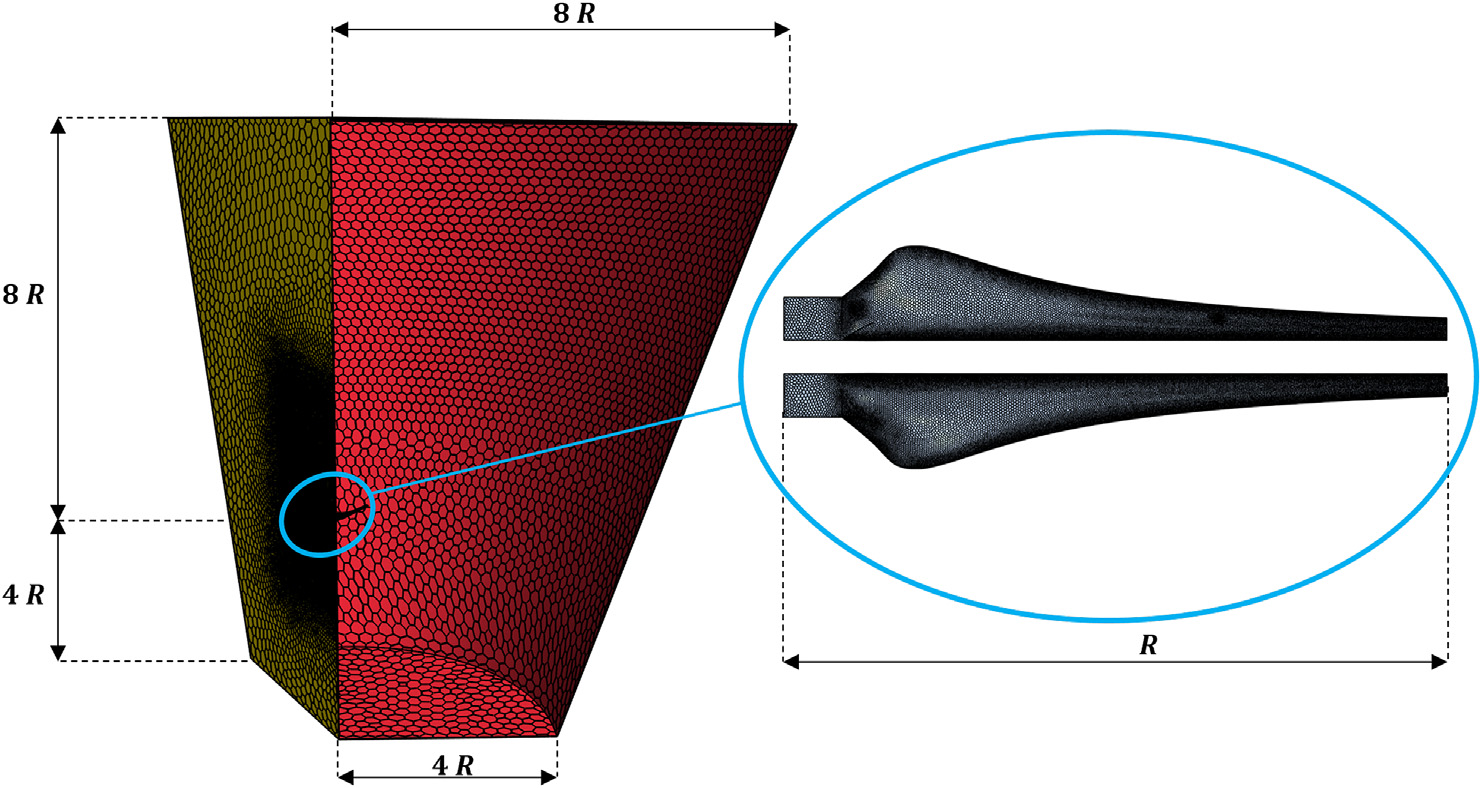
因此，流体域由一个截头圆锥构成。上游距离为4 R，下游长度设置为8 R。进口半径为4 R，出口半径为8 R，其中R为叶片半径。这些尺寸的设定旨在确保边界条件位置的影响可忽略不计。

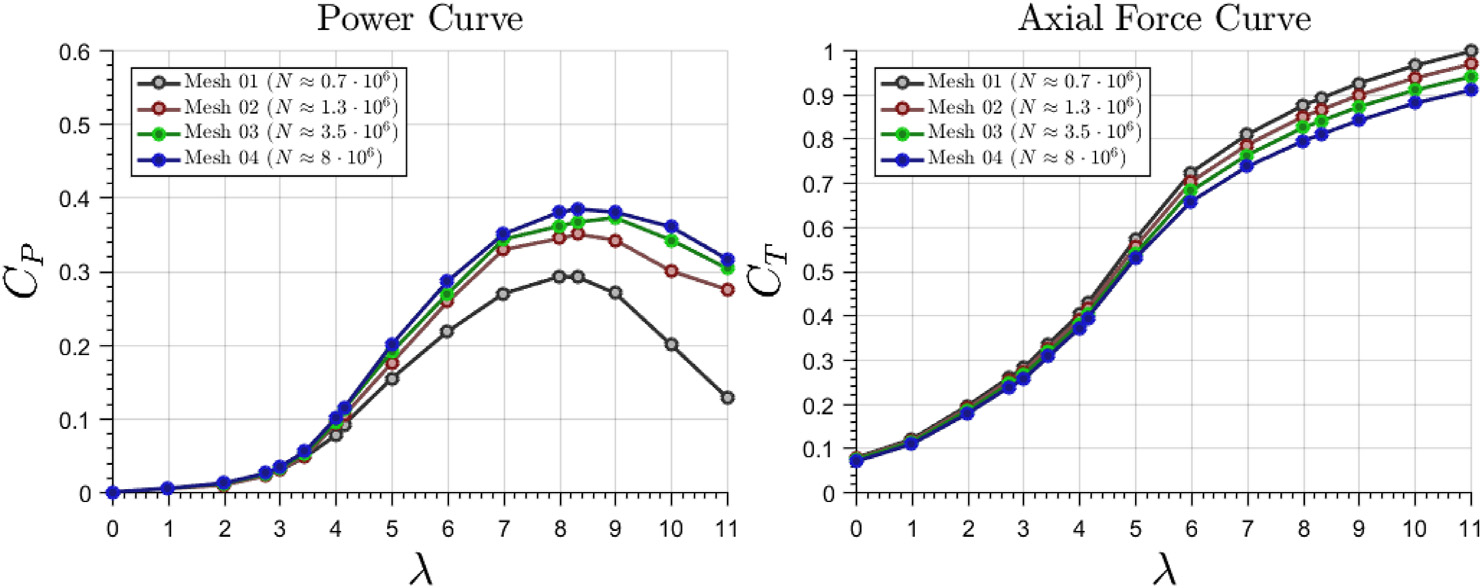
为了确保结果不依赖于所选择的离散化方案，针对四种不同的网格计算了无量纲功率和轴向力曲线。图4显示了功率（左）和轴向力（右）系数随网格单元数量增加的变化情况，N。注意，在 λ取值较低时，功率和轴向力曲线均在单元数量相对较少的情况下达到了网格无关性；而当 λ> 5时，由于流体附着在叶片上，所需的单元数量更高。

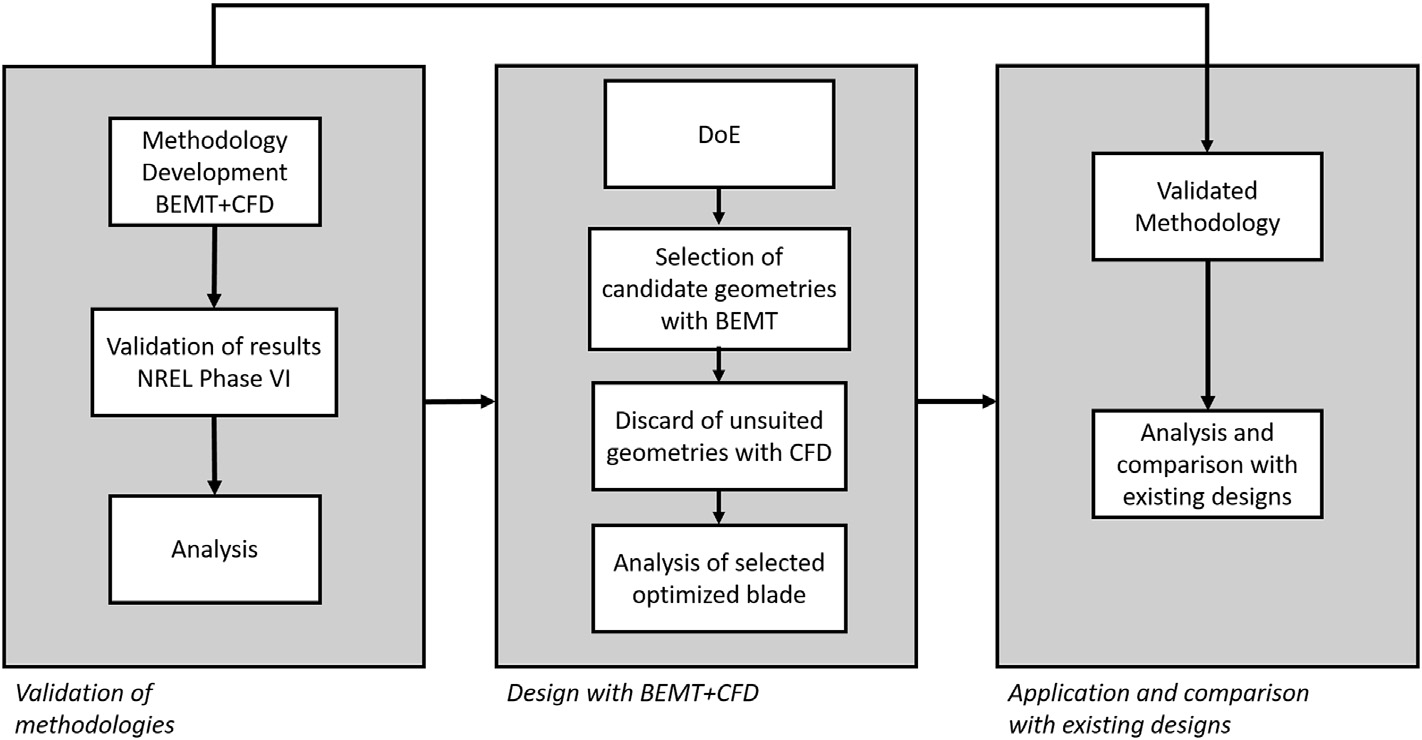
图4 表明，对于第四个研究的网格，可以认为已实现网格无关性。为确保结果可重复，需注意此配置对应叶片上的平均网格尺寸约为0.005R 和远离叶片处的最大尺寸为0.25 R。在计算叶片上的力和力矩时，叶片上游及尾流区域的流动分辨率至关重要（Leishman，2006）。因此，在尾流区域设置了尺寸为0.02R的网格加密区，最终生成包含N ¼ 8120000 个单元的多面体网格。

为了获得风力涡轮机的无量纲功率曲线，设置了恒定速度入口 Vz ¼ 8 m s⁻¹，并参数化地改变转速。在此情况下，基于相对叶尖速度的雷诺数 Re ¼ ρR √(Vz² + (ΩR)²)/μ 在区间 [2×10⁶, 6×10⁶] 内变化，该值足够高，可忽略雷诺数对摩擦系数的影响。

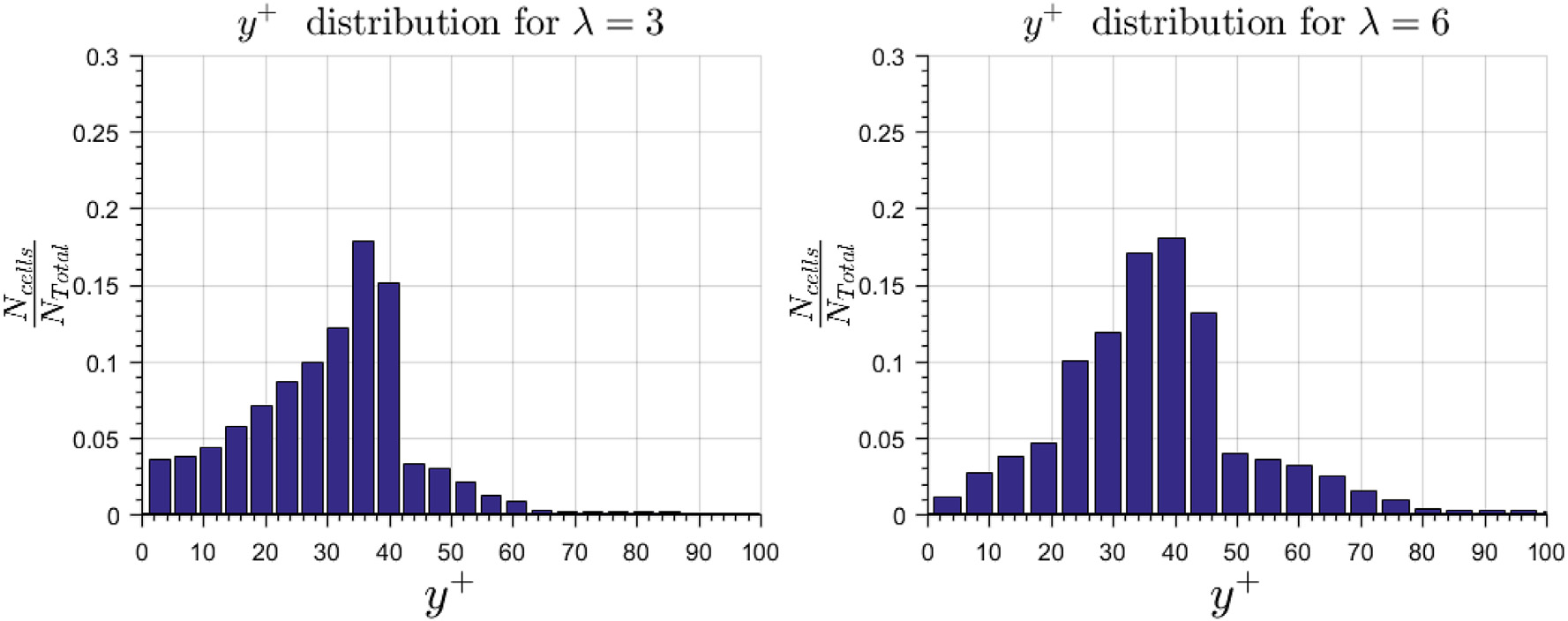
壁面 y⁺ ¼ yuτ/ν在所研究的几何结构大部分区域中均确保大于30，因此可以使用对数壁面函数（Barenblatt，1993）。从图5中可以确认这一点，该图显示了壁面y⁺的相对单元分布在 λ ¼ 3（左）和 λ ¼ 6（右）的情况。此处可计算得出，即使对于λ ¼ 3，超过70%的壁面单元的y⁺值介于30到100之间。

当前数值方法论在NREL Phase VI双叶片风力涡轮机的结果上得到验证后（见第3.3节），相同的规格被应用于最优的三叶片低功率风力涡轮机，这将是本文的主要研究目标。因此，该情况下的网格示意图如图 6 所示，所有提及的加密层级可同时观察到，且截头圆锥的角度为 Δθ ¼ 120度，对应于叶片数 ¼ 3。

3.3. 模型验证

动量‐叶素理论和计算流体力学均需通过实验数据进行验证，为此根据前文所述条件对NREL第六阶段风力涡轮机进行了建模。选择该双叶片风力涡轮机的原因在于文献中针对该机型已开展的大量研究工作（（Sørensen 等，2002），（奥吉亚诺，2014））以及可获得的实验数据（（汉德等，2001），（西姆斯等，2001））。

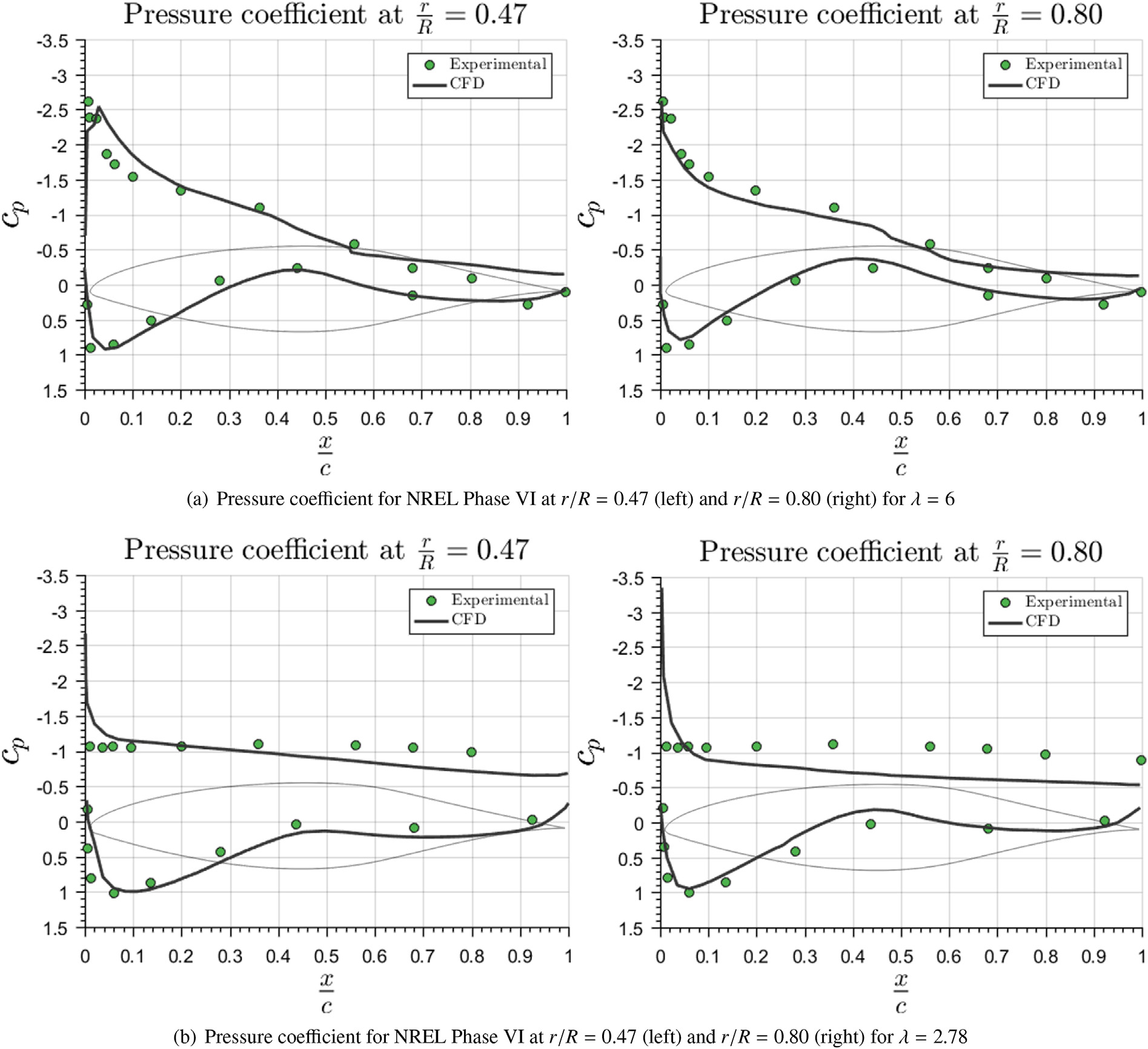
图7 显示了在两个不同径向位置处，沿叶片弦长的压强系数系数 Cp随叶片弦长的变化情况。各截面处的压强使用该处的相对风速进行无量纲化处理，方法如下：

$$
C_p = \frac{p - p_\infty}{\frac{1}{2} \rho (V_z^2 + (\Omega r)^2)}
$$

可以看出，当前的CFD计算与测量结果吻合得相当好。在λ较低的情况下，吻合程度稍差，此时局部攻角较大（曼维尔等，2009）。然而，即使在这些情况下，结果仍显示出良好的一致性。

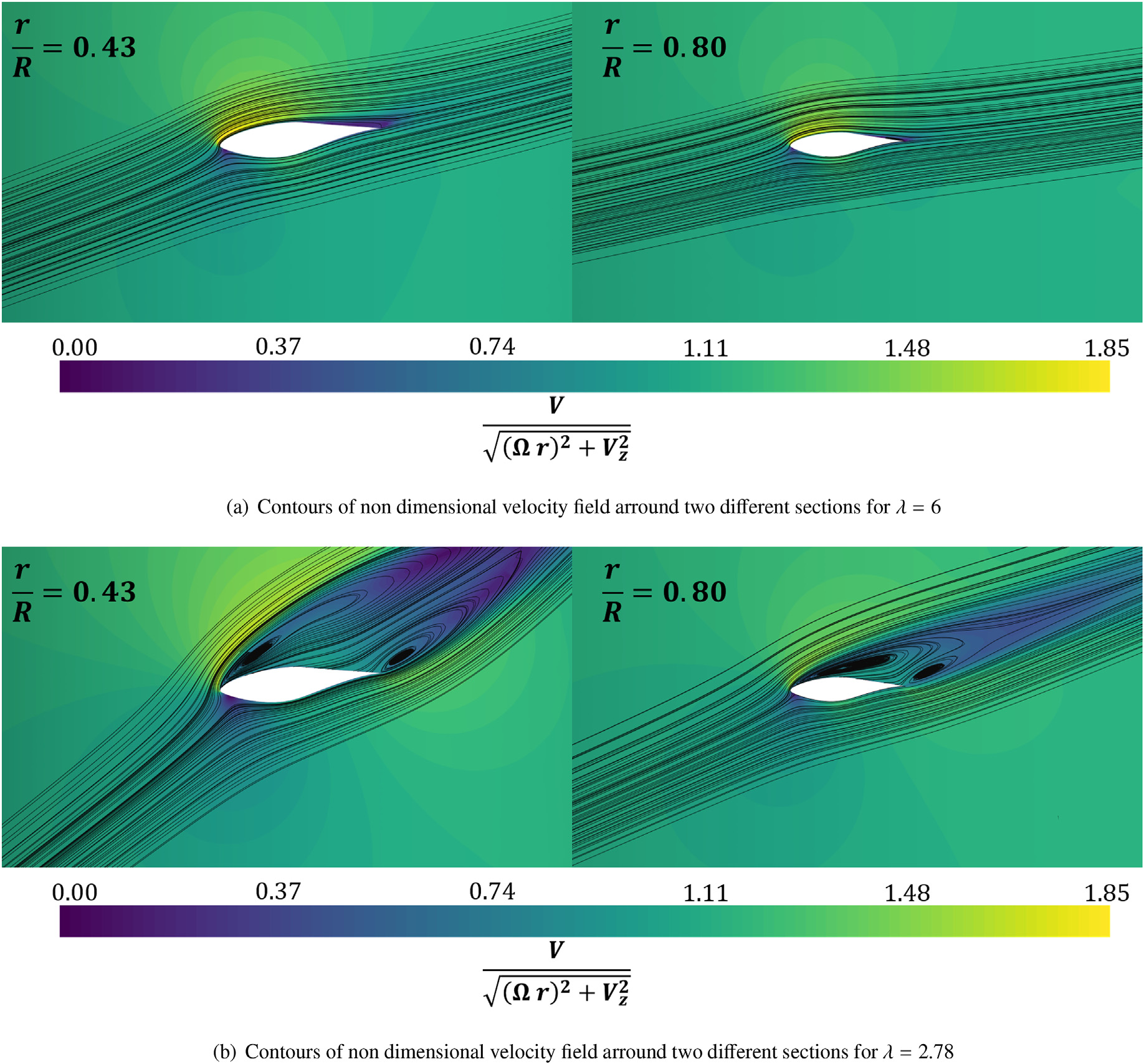
由图8中无量纲速度V* ¼ V / √((Ωr)² + Vz²) 的大小分布情况，可以很容易地解释图7所示的压力系数的变化情况。

旋转参考系fi与场流线相结合，用于与上图中所使用的相同典型翼型。注意，当 λ ¼ 6时，fl叶片上的流动是附着的，导致压力面与吸力面之间存在较大的压力降。而对于 λ ¼ 3的情况，fl这些截面上的流动发生分离，导致在吸力面上观察到几乎恒定的压力系数，如fi所示。图7(b)。

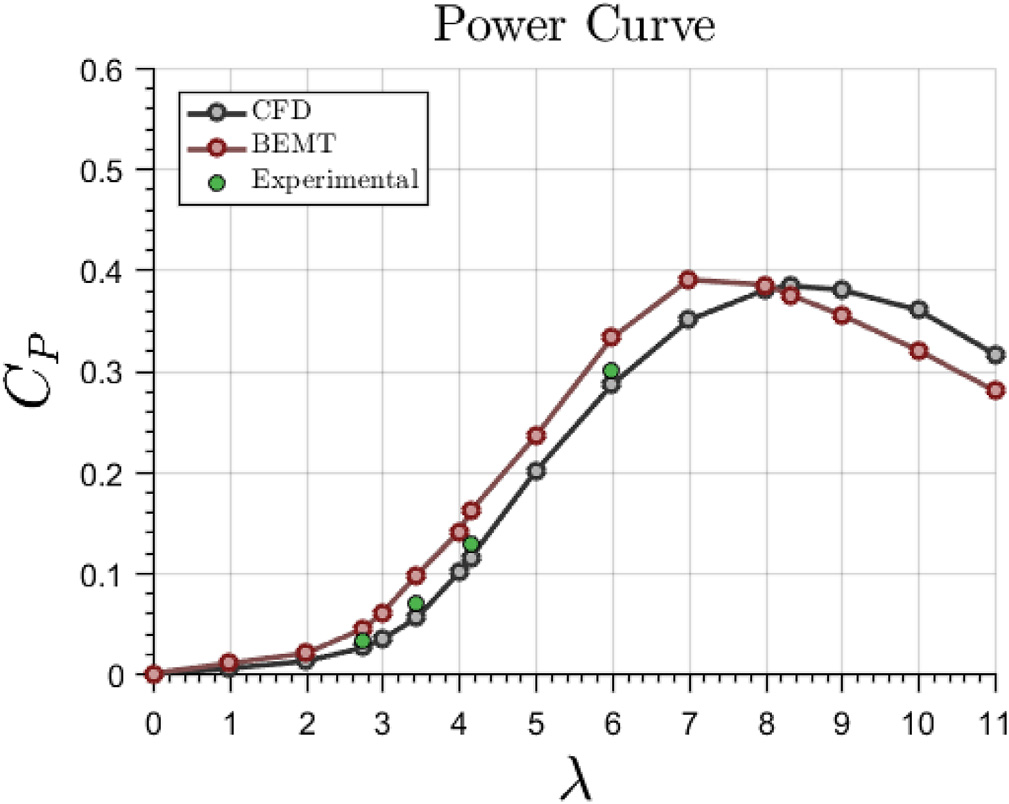
此外，图9 显示了功率系数随 λ的变化情况。可以看出，当前的 CFD‐MRF模拟结果与实验数据相当吻合。如预期一样，由于模型的局限性，动量‐叶素理论在较低的 λ值时 tends to 高估功率值。然而，该模型仍能在显著减少计算时间的情况下，对整个工作范围提供可接受的初步预测。因此，该模型被用于对可能的改进措施进行前期分析。但应注意的是，如果新设计的特征导致显著的三维效应出现，则需考虑这些效应来分析动量‐叶素理论预测的功率曲线。因此，后续使用计算流体力学方法研究了经动量‐叶素理论优化的风力机系列，以获得更真实的功率曲线。曲线对比显示，在最大功率系数的预测上差异约为3%，在最佳叶尖速比的位置上差异约为12%，这与以往研究中比较这两种方法时所报告的差异一致（普拉扎等，2015）。

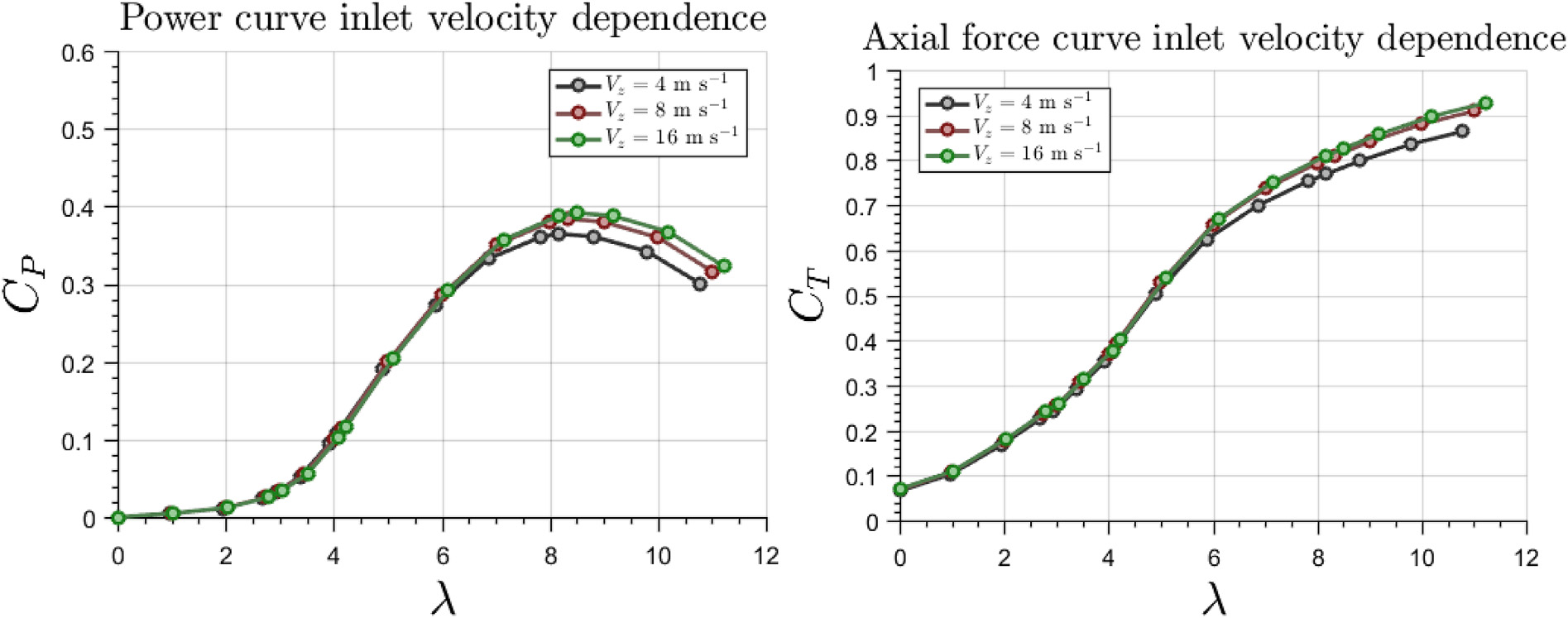
为了验证忽略雷影响的有效性，雷诺数下，NREL Phase VI 的性能曲线已在三组不同的入口速度下进行计算，覆盖了整个预期工作范围。图10显示了功率曲线（左）和轴向力 （右），对应风速为 Vz ¼ 4m/s⁻¹, Vz ¼ 8m/s⁻¹, Vz ¼ 12m/s⁻¹。可以得出结论：尽管在较高的 λ值下存在一些差异，但这些差异低于5%，因此雷诺数无关性的假设可视为足够准确。

4. 结果

4.1. 实验设计结果

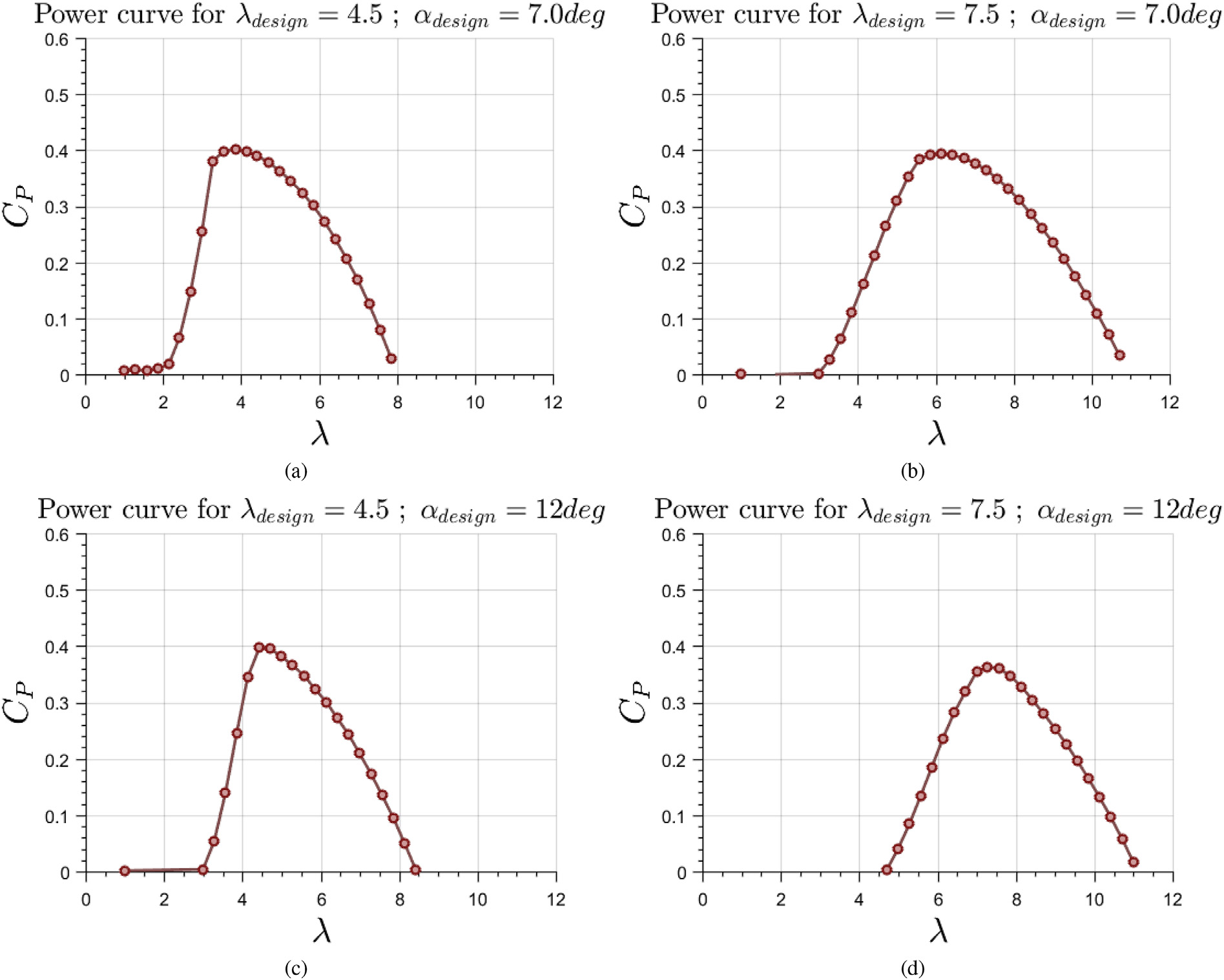
完成实验设计后，获得了一系列功率曲线。图11展示了几种典型的功率优化方案。可以看出，随着λd 的增大，曲线的左侧斜率减小。同时还可以观察到，当αd 增大时，呈现出相反的趋势。在实验设计过程中，假设叶片数量为B ¼ 3，半径固定为R ¼2.50 m。

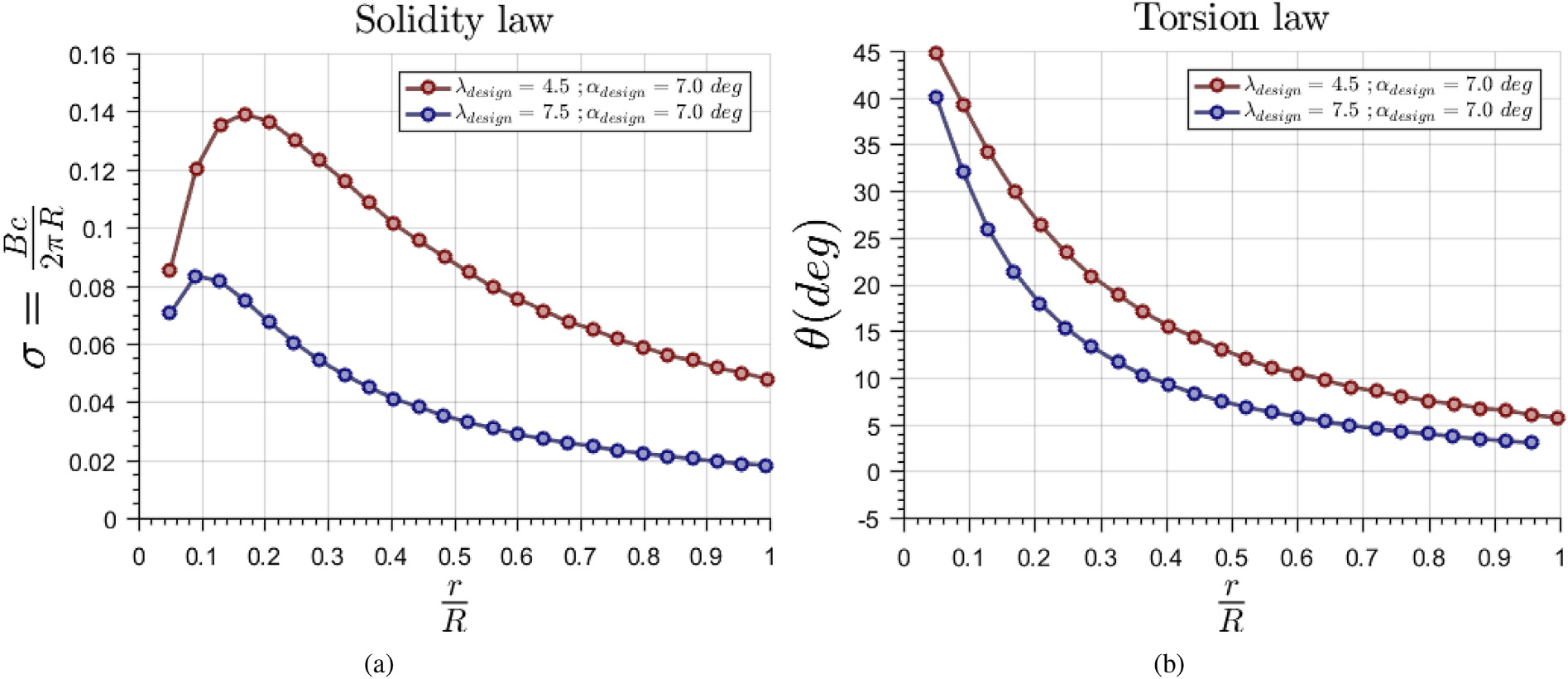
对于较大的 αd 值，功率曲线趋近于较低 λ值下的 Cp ≪ 1。从最大功率系数和可控性（见公式(11)）的角度来看，所显示的设计在 (λd ¼ 4.5；αd ¼ 7度)和 (λd ¼ 7.5；αd ¼ 7度)时均可能是有效的。然而，由于应采用的实度过高，该制造标准在第一组取值组合中未得到满足。这一点可以从图12中看出，其中这些值作为到轮毂的无量纲距离的函数被展示出来。因此，考虑从这组叶片中选择由 (λd ¼ 7.5; αd ¼ 7度)生成的情况。

上述解释仅作为一个示例，旨在说明自动筛选流程如何通过少量起始叶片（出于图示目的）实现叶片设计的缩减。将完全相同的流程应用于第3.1节所述实验设计过程中生成的全部70种可能的设计，可大幅减少需通过计算流体力学（CFD）进行评估的设计数量（本案例中最终得到5种叶片，但具体数量可能受第3.1节所述限制条件选择的影响）。

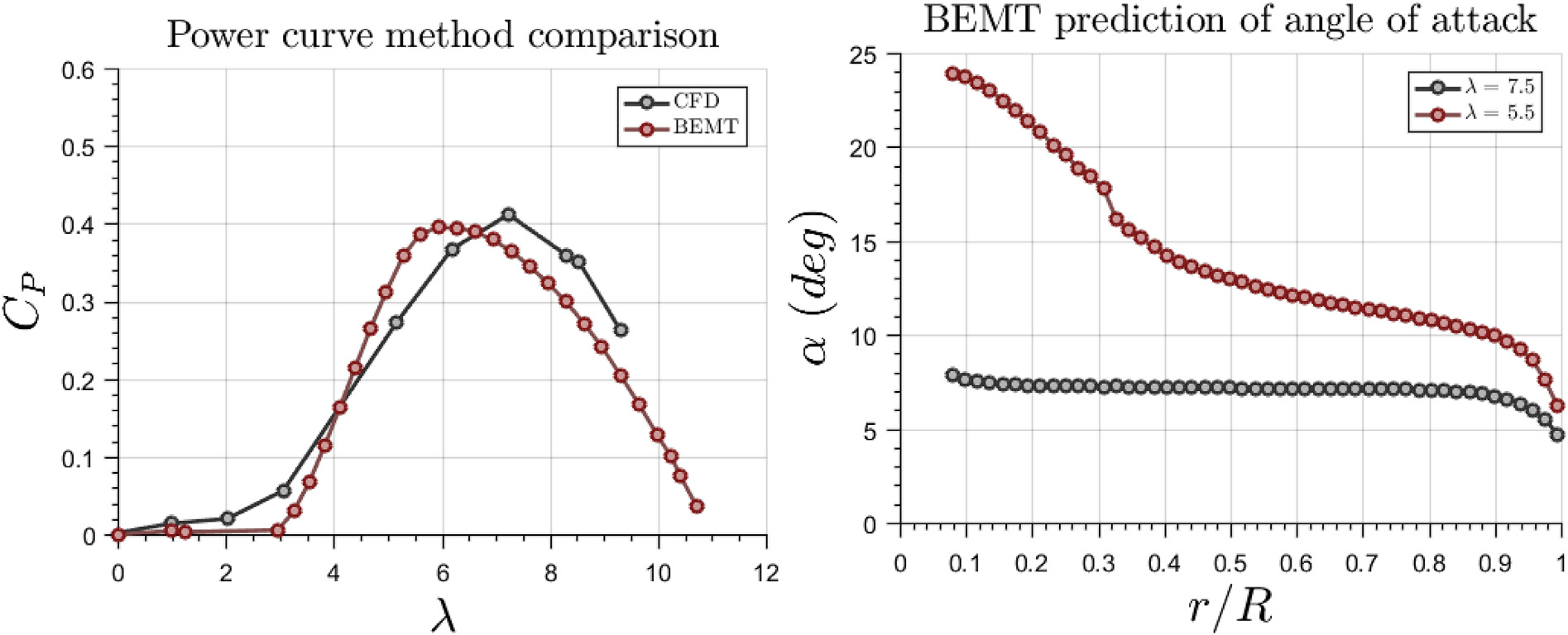
所提出的叶片设计策略使用了第3.2小节中介绍的计算流体力学模型进行分析。通过两种方法对功率系数的结果进行了比较。图13（左）显示了在设计过程中使用动量‐叶素理论与三维计算流体力学稳态计算所作预测之间的对比。可以看出，主要差异出现在最大功率系数对应的叶尖速比位置的预测上，两者相差约11%。最大CP 的值预测得较好，差异约为4%。类似其他研究人员在MEXICO转子空气动力学研究中也已报道过计算流体力学与动量‐叶素理论之间类似的差异（普拉扎等，2015）。

对图13（左）所示的功率曲线进行目视检查，可以观察到在 λ较低值时的定性差异似乎比图9验证研究中观察到的差异更加明显。这主要是由于当前提出的叶片设计的功率曲线形状较为狭窄。尽管最大功率系数的位置以及最大系数本身的差异与第3.3节中展示的差异处于同一数量级，但曲线较高的左侧斜率使其更为明显。

此外还可以观察到，对于较低的叶尖速比(λ ∈ [4, 5])，动量‐叶素理论倾向于高估功率系数，这主要是由于该模型未包含三维失速延迟现象所致。此外，可以看出功率系数曲线的左侧斜率被动量‐叶素理论高估了。然而，从可控性的角度来看，这种差异被 λ的增加所补偿，符合公式(11)。因此，动量‐叶素理论对于所进行的实验设计而言已足够准确，这一点将在后续展示。

低 λ 值下功率系数预测的差异（以及由此导致的功率曲线预测的差异）斜率图13（右）中可解释。在该图中，针对两个不同的叶尖速比值，比较了动量‐叶素理论预测的攻角：一个值为 λ¼ 7.5 ¼ λdesign 和 λ ¼ 5.5< λdesign。注意，对于前者，在大部分叶片上，攻角α ≈ 7.0度 ≈ αdesign几乎保持恒定。当 λ的值减小时，如预期一样，预测的攻角趋于增大。由于根部与叶尖相比，与NREL Phase VI相比，攻角在根部的增加更为急剧。在此条件下产生了显著的攻角梯度，加之处于失速条件下的运行，将导致出现非常重要的三维效应，而当前的动量‐叶素理论并未考虑这些效应。

还可以注意到，对于这些几何结构，如果未对动量‐叶素理论施加额外的三维修正，则在非常低的叶尖速比 (λ ≤ 3) 下的预测结果不能被视为足够准确，因此，在这些条件下应使用计算流体力学或实验测量以获得有价值的结果。

4.2. 与其他设计的对比

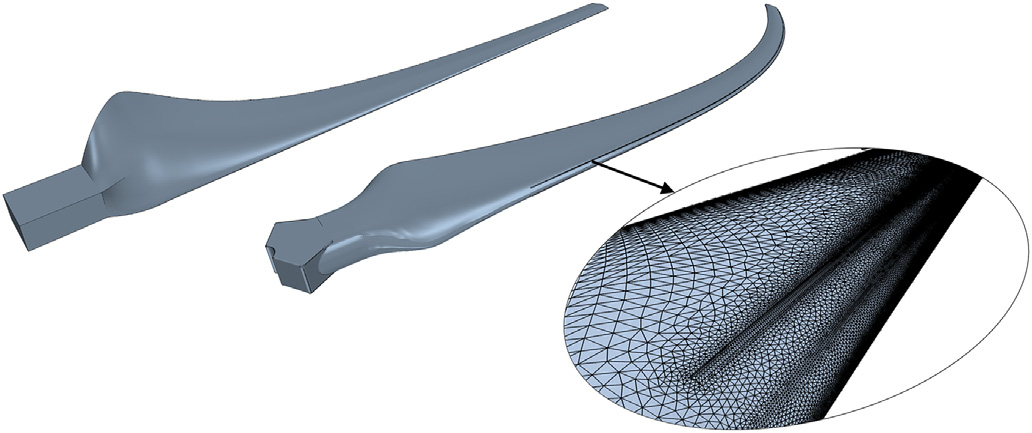
如前所述，一旦通过实验设计生成并选定一种设计，就必须将其性能与已知的可用设计进行研究和对比分析。为此，选用了低功率风力涡轮机Skystream的叶片，因为该型号是当前低风速风能发电市场中的领先产品之一。商用叶片的几何结构已被数字化，以便进行CFD计算。还需注意的是，如前所述，由于叶片具有水平曲率，当前的动量‐叶素理论方法论不能直接适用于此问题。图14显示了所提出的当前设计（左）与 Skystream几何结构（中）之间的几何对比。图14（右）展示了 Skystream几何结构的放大图，其中可在叶片大部分径向坐标处观察到几何凸起。

上述提到的几何特征将作为涡流发生器（VG），其目的是影响边界层的行为。由于这类产品通常受到湍流强度和三维流动的影响，层流边界层与湍流边界层之间的转捩位置预计不会起主导作用。因此有必要研究涡流发生器（VG）对能量产出的影响，同时也研究了去除涡流发生器后的 Skystream几何结构。

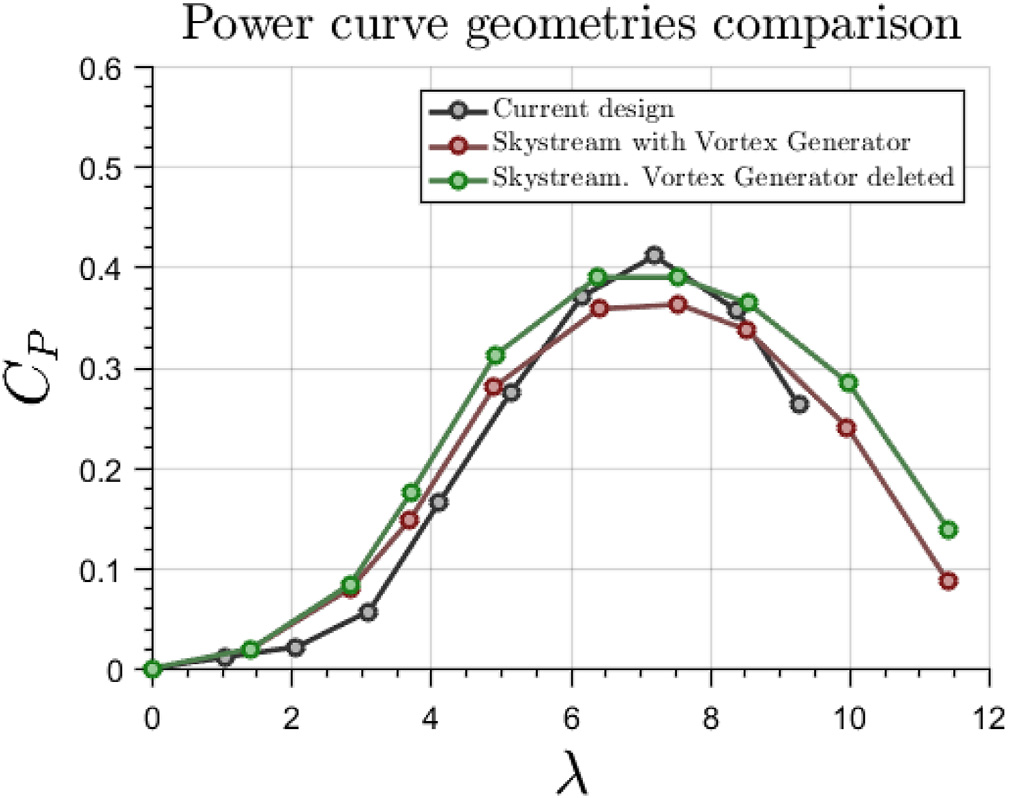
为了实现这一目标，图15 展示了所提及几何结构的计算流体力学模拟得到的功率曲线。可以看出，当前设计显示出更高的在工作区附近较宽的范围内（从 λ ¼ 6.2 到 λ ¼ 8.5），功率系数的取值。对于 λ< 6.2，当前设计表现出明显的斜率和较低的CP值，有助于在Vz较高时实现更好的稳定性。此外，与商用设计相比，CP的峰值提高了14%。

将带涡流发生器（VG）与不带涡流发生器的商用设计进行比较也具有重要意义。在整个风力涡轮机工作范围内，带VG的设计表现出较低的 CP值。由此可以得出结论：该涡流发生器似乎并未从能量产生角度提升风力涡轮机的性能。然而，整个工作范围内功率系数的降低可能带来更优的稳定性表现。

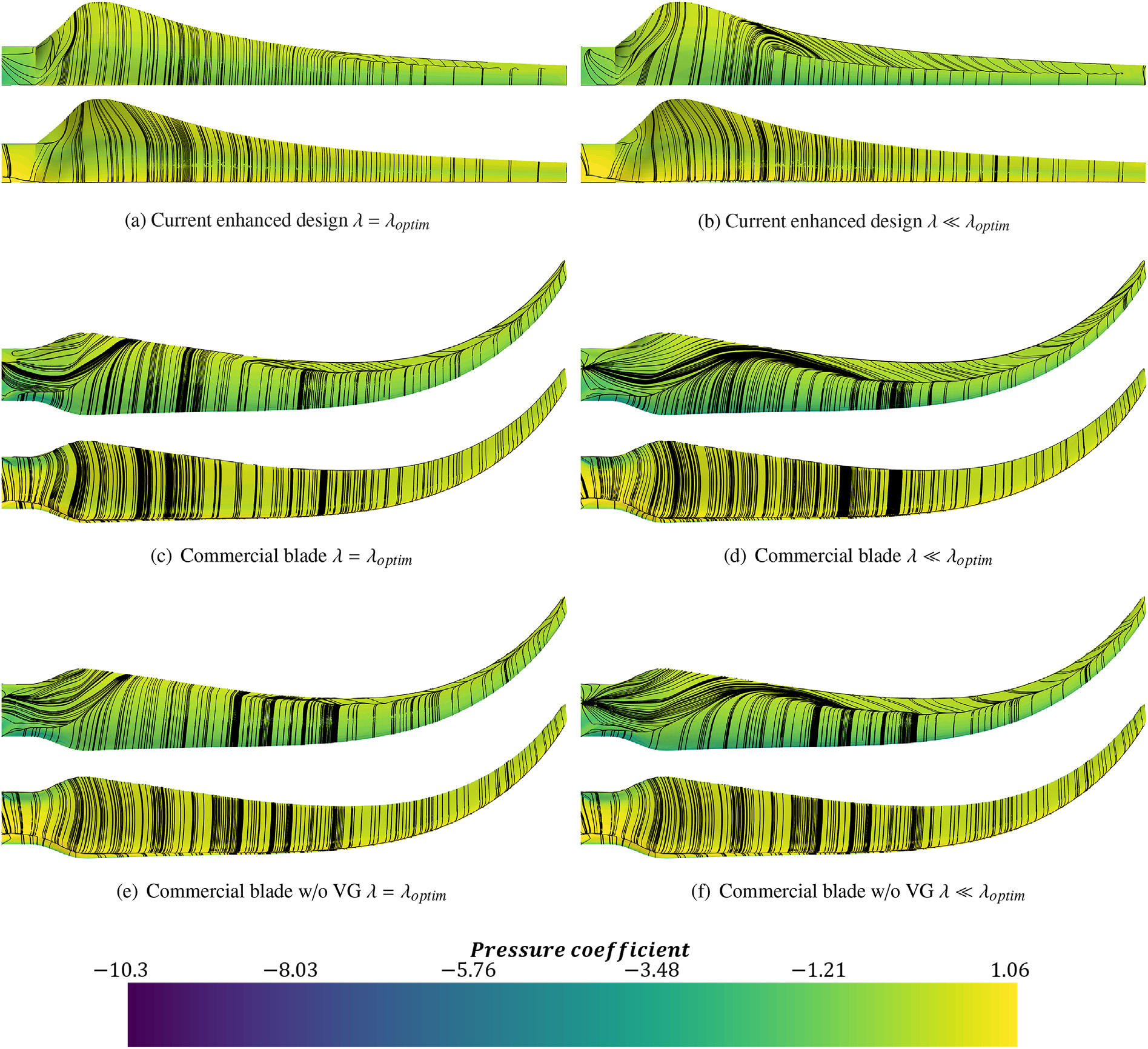
不同几何形状之间的压力系数差异与在不同运行条件下各叶片吸力面和压力面的压力分布密切相关。图16 显示了按照公式(13)定义的压力系数分布。对于每个叶片，吸力面和压力面分别显示在上方和下方。注意，在所有情况下，压力面上的压力系数值均较高。当λ≈λopt时，吸力面上的压力系数在叶片前缘附近表现出明显的最小值。

在图16 中，表示了在每个叶片点处与壁面剪切应力相切的线。这些线发生突变的位置代表了气流突然分离的区域。对于所有设计而言，总体趋势是：当λ取值较低时，气流分离的区域 tends to be increased。这是由于在这些较低的旋转速度下出现了较高的局部攻角（见公式(1)）。

关于不同设计方案之间的比较，可以看出，对于当前增强设计（图16（a）和（b）），叶片表面发生分离的区域比商用叶片情况更小（图16（c）和（d））。在商用叶片中移除涡流发生器（图16（d）和（e））显著减小了分离区域，特别是对于较高的叶尖速比。这一现象与无涡流发生器的叶片 tends to 产生更高功率密切相关，尤其是在 λ 值较高时。

在分析了所提出的当前设计和商用叶片的无量纲特性后，有必要对由公式(11)的左斜率条件所表示的可控性参数进行验证。此外，还将说明有必要进行CFD分析，以修正其他候选几何结构的BEMT预测，从而排除那些预计会出现严重可控性问题的几何结构。

正如之前所述，在开发过程中通过实验设计获得了多个候选几何形状。特别是，除了之前提到的提出的设计（应记住该设计是通过使用参数λd ¼ 7.5和αd ¼ 7deg生成的）之外，还考虑了其他几何结构。其中一个示例是可通过应用参数λd ¼ 6.5 和 αd ¼ 6deg重构的设计。

无量纲功率曲线（左）和无量纲扭矩曲线 (CQ ¼CP/λ)（右）在图17 中展示了该替代设计与当前设计及商用叶片相应曲线的对比。可以看出，该替代设计的功率系数略高于所提出的叶片。此外，请注意功率系数的左侧斜率显著更低。直观上，人们可能会将功率系数的低斜率归因于更易于控制，但由于有量纲功率与来流流体速度呈三次方关系（见公式(11)的推导），情况并非如此。因此，在高风速条件下应用机械制动时，应确保功率系数（以及相应的扭矩系数）迅速下降，以补偿速度的增加。

这一事实可以通过数值应用轻松理解。一旦获得了叶尖速比下的无量纲功率和扭矩系数，并且考虑到其对雷诺数的依赖性为二阶（见图10），在给定风力机半径的情况下，对于任意组合的转速 Ω和风速Vz，均可直接得到有量纲功率。

失速调节型风力涡轮机通常遵循的一种典型控制策略是在低风速条件下以最大功率系数运行，λ ¼ λopt当风速超过某一特定值时保持恒定转速Ω ¼ Ωmax（Muljadi 等人，1998）、（Muljadi 等人，2000）和 （Macquart 和 Maheri，2019）。当风速进一步升高时，必须施加制动转矩以停止风力涡轮机。为确保这一点可行，发电功率和扭矩均不得随风速无控制地增加。

因此，图18 展示了基于图17中叶片在正常环境条件下（ρ∞ ¼ 1.225 kg/m³）运行时的有量纲功率和扭矩预测结果。假设这些叶片尺寸相同，叶片半径 R ¼ 2.50 m，并在达到最大功率系数的工况下运行，直至转速超过 Ωmax ¼ 170 rpm。当风速更高时，转速保持不变，因此 λ将随之下降。

可以观察到，当风速低于 Vz ¼8 m s⁻¹ 时，三个叶片在功率和扭矩方面的表现非常相似。然而，当风速增加时，被弃用的设计的功率会以不可控的方式上升。这可归因于左斜率的值较低，对应较高的扭矩系数。商用叶片也表现出类似的趋势，尽管变化较缓慢。提出的设计显示，当风速超过 Vz ¼12 m s⁻¹ 时，功率和扭矩均保持在有限范围内，因此有可能实现风力涡轮机的停机。

之前的论述仅针对本研究所获数据的直接应用。然而，结论可推广至其他控制律。图19 展示了采用替代设计的风力涡轮机在不同最大转速（50 转/分；100 转/分和 200 转/分）下使用不同控制律时的性能。可以认为，在较低转速值（50 转/分）下即可实现对风力涡轮机扭矩的完全可控，尽管此时扭矩和功率曲线仍为单调递增。然而，这是以大幅降低发电功率为代价的，因为风力涡轮机始终在远离 λ的最优值状态下运行。若将转速提高至 100 转/分，则只有在风速超过 20 m s⁻¹时，才能获得约 2.5 kW 的可用功率。

5. 结论

本研究提供了一种风力涡轮机叶片设计方法论，可被视为一种灵活准确的工具。该方法可作为更复杂设计开发的基础，因为本文已对其进行了完整验证，并讨论了所用工具之间的差异。例如，该方法论可用于探索约束的敏感性，根据设计目标增加或删除约束条件，甚至可基于当前提出的约束条件构建以目标函数最小化为基础的优化工具。特别是，该方法已应用于低功率失速调节型风力涡轮机的设计。

该方法论结合了一整套设计实验，采用动量‐叶素理论（BEMT）这一低计算成本工具，以选择具有最佳性能与控制的叶片几何形状。此外，还采用了计算流体力学（CFD）方法，精确考虑三维流动效应，从而能够剔除那些最初符合BEMT、但在考虑三维效应后不易于控制的几何结构。

该组合方法论已通过NREL第六阶段风力涡轮机公共数据目录中的实验结果进行了验证。结果已成功在风力机功率方面以及沿完整叶片在不同径向截面的压力系数方面进行了比较。

所提出的BEMT设计流程包含了对功率曲线形式的额外限制，以获得不仅能够最大化功率系数，而且能够在失速调节型水平轴风力机设计中考虑可控性问题的叶片几何形状。结果得到了可行叶片设计的精简集合，从而可以对其开展CFD计算，并最终选择一种叶片，该叶片既能提高最大功率系数（相较于商用设计），又能实现近乎平坦的无量纲功率曲线，适用于简单控制律。

对提出的设计的预测行为从发电功率和可控性方面进行了分析，并与在相似工作条件下对现有商用风力涡轮机的预测结果进行了比较。该对比表明，新设计能够在提高风力涡轮机安全运行速度范围的同时，获得更高的功率值。

此外，还研究了安装在叶片前缘附近的涡流发生器（VG）对性能与控制能力的影响。研究发现，所提出的VG方案似乎会对最大功率输出产生负面影响。此外，VG会影响流动分离现象，从而影响叶片控制风力涡轮机旋转速度的能力。

已经展示了如何结合叶素动量理论和雷诺平均纳维‐斯托克斯方法，以充分利用每种模型的相关能力：
- 动量‐叶素理论（BEMT）能够在较低的CPU成本下获得大量候选方案，并剔除那些明显不符合性能要求的候选方案。然而，它未考虑三维效应，而这些效应在低叶尖速比（TSR）值下的性能准确预测中可能具有重要意义。
- 在本研究中，采用雷诺平均纳维‐斯托克斯方程（RANS）精确获取少量预选设计方案的性能表现，并剔除不满足性能和控制要求的方案。

最后，无量纲功率曲线的左斜率已被证明是成功设计失速调节型风力涡轮机的关键参数。事实上，将该参数作为相对简单的设计约束加以考虑，能够生成一种叶片几何结构，其提供的功率高于类似设计，并且能够在较宽范围的风速下安全运行。