树状数组求区间最大值 （单点修改）

以前一直把树状数组当作求前缀的工具，但事实上，树状数组是一种分块的方式，因为分块的方式比较独特，所以在求前缀的过程中非常方便；

树状数组的实现原理就不讲了，这里要特别说明的是，lowbit(x) 不仅可以表示区间分块对应存储前缀的位置，同时还能够表示一个区间的长度，这个长度在求区间最大值的时候起到比较重要的左右，也是我之前没想到的部分；

文字说明：

求区间最大值 和 求区间和有很大的不同，因为树状数组求前缀和十分方便，所以通过 sum (R) - sum (L-1) 就能得到一个区间的和；那么区间最大值怎么求？

假设要求  L 到 R 的区间最大值，我们分块仍然是根据lowbit(x) 的方式分，对应分块的最大值也很容易想到，就是求前缀和中累加的部分改成 max () 就行了；

查询： 如果我们根据lowbit 的规则从右向左求区间的最大值，所求的结果是 1 到 R 这个区间的最大值，显然答案可能是不正确的； 我们如何避开  1 到 L-1 这个区间？

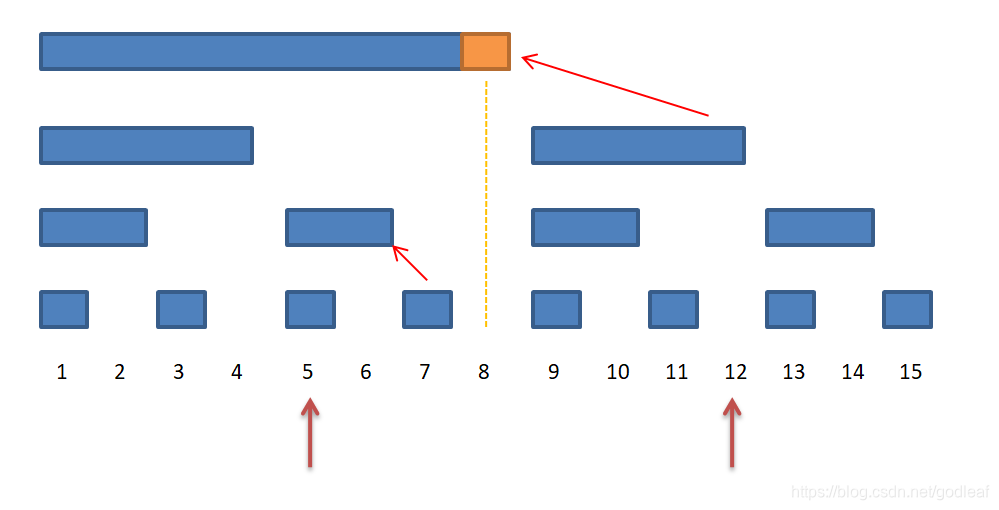
我们根据lowbit的规则，从右向左遍历区间块，如果是区间是我们要考虑的范围内就取这个最大值，如果发现当前的区间超出我们要考虑的范围就只取当前区间最末尾的值，然后lowbit - 1，然后继续从右向左遍历，直到所有区间取完为止。

根据上图的步骤，下标为12的这个位置是 9 到 12的最大值，我们能通过lowbit知道当前区间的长度是多少，由此能知道当前区间是不是在我们要考虑的范围内；当遇到下标为8，区间长度大于当前我们要考虑的长度时，我们就只取最末尾的值，也就是对应数组a[8]，lowbit - 1 到下标为7这个位置后继续从右向左判断，直到结束。 从图中可以很容易发现，以这种方式遍历，能把所有我们需要考虑的部分都遍历了一遍。

下面这题是求区间最大值的模板题：HDU-1754 

#include <iostream>
#include <cstring>
#include <cmath>
#include <algorithm>

using namespace std;

typedef long long ll;
const int Maxn = 2e5+10;

int a[Maxn], h[Maxn], n;  // a[] 数列的值，h[] 区间最大值

void add (int x, int val) {
	while (x <= n) {
		h[x] = max (h[x], val); 
		x += x&(-x);
	}
}

int query (int L, int R) {
	int ret = 0, len = R-L+1;
	while (len && R) {  // len 是当前还需要判断的范围长度，R是对应区间最大值的下标
		if (len < (R&(-R))) {
			ret = max (ret, a[R]);
			R--; len--;
		} else {
			ret = max (ret, h[R]);
			len -= (R&(-R)); // 不断的缩短要判断的区间长度
			R -= (R&(-R)); 
		}
	}
	return ret;
}

int main (void)
{
	int m;
	while (scanf ("%d%d", &n, &m) != EOF) {
		memset (h, 0, sizeof (h));
		for (int i = 1; i <= n; ++i) {
			scanf ("%d", &a[i]);
			add (i, a[i]);
		}
		char op[2], b[10]; int x, y;
		while (m--) {
			scanf ("%s%d%d", op, &x, &y);
			gets (b);
			if (!strcmp (op, "U")) {
				a[x] = y; add (x, y);				
			} else {
				printf ("%d\n", query (x, y));
			}
		}
		
	}
	return 0;
 }