计算几何小结_l2投影-优快云博客

本文链接：https://blog.youkuaiyun.com/gmh77/article/details/89231820

定义

计算几何区别于传统解析几何，是用点和向量之类的与坐标有关的东西来乱搞
点：坐标为(x,y)
向量/线段/直线：两个点，向量有方向，直线无边界
（其实写起来都一样）
其它以后再说

叉积

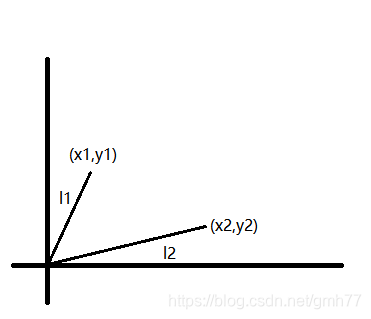
在这里插入图片描述
向量l1、l2（l2在l1顺时针方向且夹角<180°）的叉积为x₂y₁-x₁y₂，几何意义是l1、l2构成的平行四边形面积

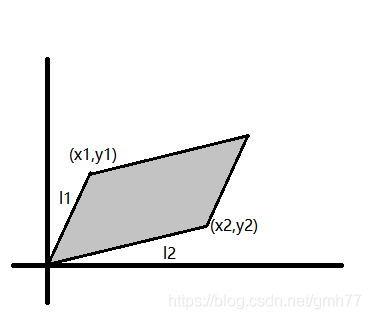
证明随便yy一下~~其实我也不会~~

求三角形面积

平行四边形面积/2=叉积/2

判断向量方向

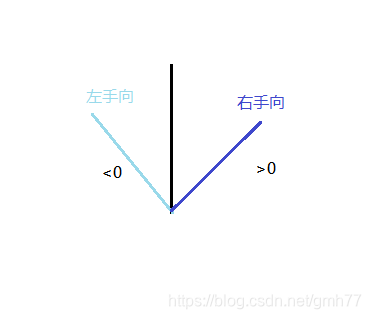
如果叉积(l1,l2)>0则l2在l1右手向（顺时针），<0则在左手向（逆时针），=0则共线
在这里插入图片描述

点积

向量l1、l2的点积定义为x₁x₂+y₁y₂，几何意义是len(l1)*len(l2)*cos(θ)
就是l1的投影长度*l2的长度
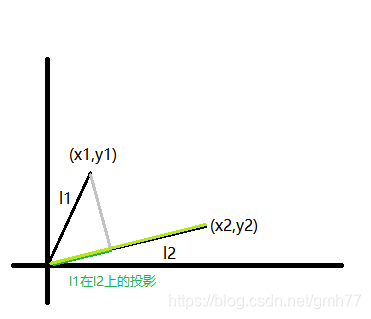
在这里插入图片描述

点到直线距离

点积/len(l2)=len(l1在l2上的投影)
然后勾股算出距离

直线交点

（线段不一定要相交，只要所在直线相交就能求出交点）
为了方便叙述，下文假设两个向量相交（前提是所在直线相交）
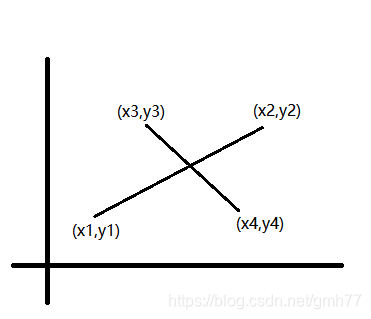
在这里插入图片描述
显然可以用叉积算出两个平行四边形的面积
（注意要同正或同负即1-3*1-2/1-2*1-4，这样比才为正数）

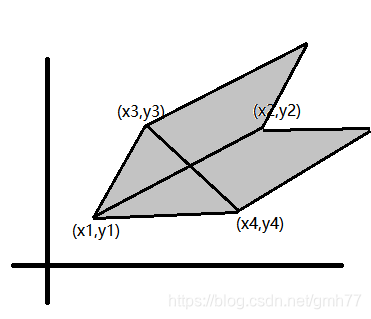
面积比即为两条高的比，也等于交点到线段两点的比
于是可以根据两条线段的比算出一条线段占总长度的比
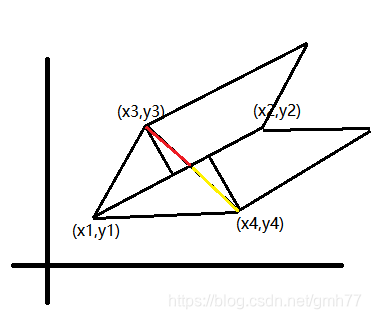
在这里插入图片描述
然后分别投到x轴y轴上，便可计算交点的坐标

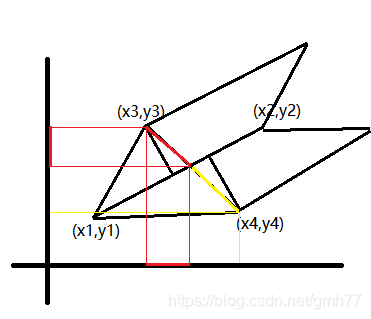
设红色和(红+黄)两条线段长度比为k
如图，交点坐标为(x3+k*(x4-x3),y3+k*(y4-y3))
有可能长度为负，但不影响结果

判断线段平行

求交点时可能会出现线段平行的情况，考虑如何判断
随便画个图发现，求出的两个面积相加为0
例如(x1,y1)(x2,y2)和(x3,y3)(x4,y4)平行，则叉积(1-2,1-3)+叉积(1-4,1-2)=0（因为要在相交时同号，所以要顺着一个方向求面积）
那么叉积相加为0则平行

半平面交

给出若干条直线，求这些直线所围成的多边形
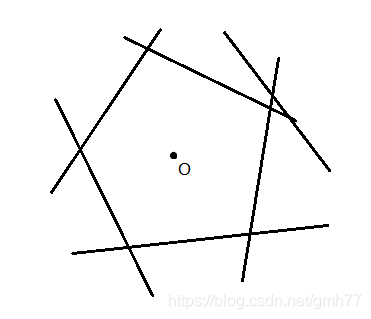
在这里插入图片描述
一种很显然(并不)的做法是把所有直线排序然后双端队列维护直线
可以用斜率来排，但可能有误差
个人做法是把线段的左端点平移到原点，按照新的右端点来排序
显然这样做是对的，但只有一个点也不太好排
可以用arctan来求斜率，根据象限特判
但这样不好搞x=0的点
所以个人用了叉积排序。为了避免出现转圈的情况，先按照象限排序，后按照叉积排序
对于斜率相同的直线取离原点最近的

对于新加入的一条直线，显然在直线外侧的交点连同直线都没用了，在队列中删去
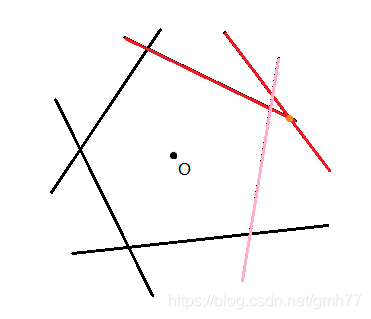
在这里插入图片描述
不过这样可能会出现螺旋的情况：

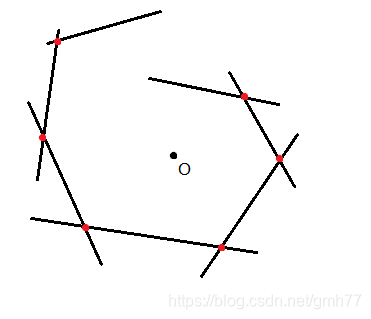
于是对于一条新加入的直线，判断它与上一条直线的交点是否在队头直线的内侧，否则不加

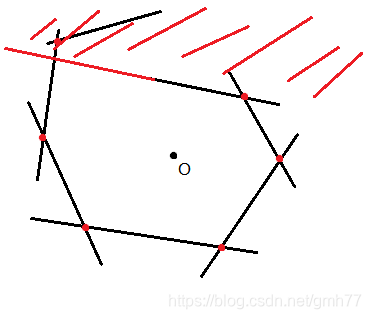
最后把头尾相交，所有的交点即为整个多边形

例题1

jzoj5546. 【WC2018模拟】家&jzoj6093. 【GDOI2019模拟2019.3.30】星辰大海
Description
在这里插入图片描述

Input
在这里插入图片描述

Output
在这里插入图片描述

Sample Input
4
4
4
1 1
0 0
2 0
1 2
3
1 0
0 0
2 0
3
1 1
0 0
2 0
5
0 5
0 0
1 10
5 15
-5 15

Sample Output
2.0000000000
0.0000000000
2000000000000.0000000000
13.3823529412

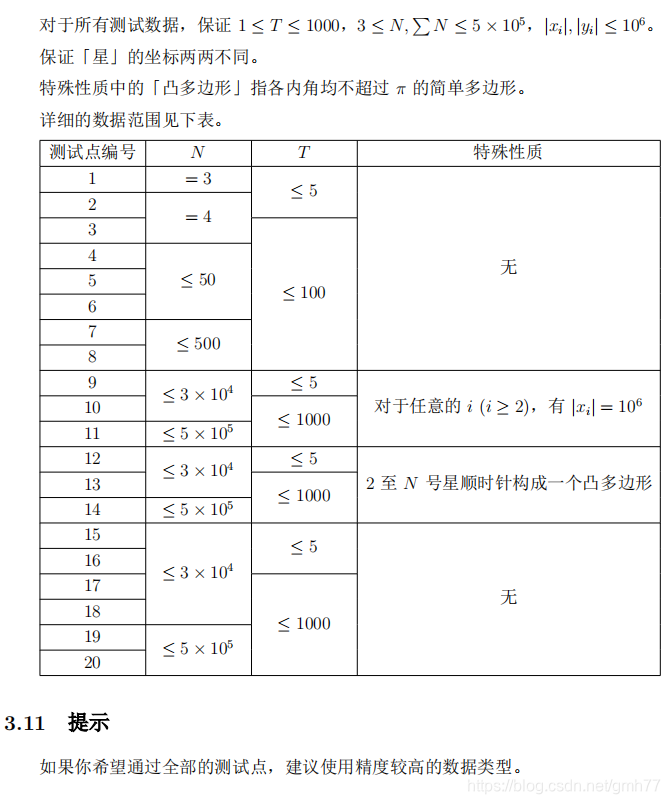
Data Constraint
在这里插入图片描述

题解

一种比较清(sha)真(bi)的做法，用凸壳+三分求出每个点最靠近点1的两条直线然后半平面交
这样显(ying)然(gai)是对的，但太麻烦
题解做法是将相邻的点连边，然后再加上离每个点最远（夹角最大）的两个点，接着半平面交
正确性见题解

code

清真码量
~~终于知道计算几何为什么这么鬼畜了~~然而这还只是基本操作

#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define sqr(x) ((x)*(x))
#define abs(x) ((x)>0?(x):-(x))
#define inf 1000000
#define E 0.00000000000001
using namespace std;

struct p{
	long double x,y;
	int s;
	p (long double _x=0,long double _y=0) {x=_x,y=_y;}
};
struct P{
	p s1,s2,S;
	long double Jl;
};
long double AA[500001];
p a[500001];
P ans[1500001];
int d[1500001];
p D[1500001];
int T,NUM,n,i,j,k,l,len,Len,h,t;
long double X,Y;
bool Bz=0;
p Swap,O;
long double Ans,A,B,C,F;

inline int getint() { char c; int ret=0, k=1; for(c=getchar(); c<'0' || c>'9'; c=getchar()) if(c=='-') k=-1; for(; c>='0'&&c<='9'; c=getchar()) ret=ret*10+c-'0'; return k*ret; }
void swap(long long &x,long long &y)
{
	long long z=x;
	x=y;
	y=z;
}

long double cj(p c,p a,p b) //>0时a在b的逆时针方向
{
	return (b.x-c.x)*(a.y-c.y)-(a.x-c.x)*(b.y-c.y);
}
long double Cj(p a,p b) //>0时a在b的逆时针方向
{
	return b.x*a.y-a.x*b.y;
}
long double dj(p c,p a,p b)
{
	return (a.x-c.x)*(b.x-c.x)+(a.y-c.y)*(b.y-c.y);
}
p jd(P a,P b)
{
	long double s=cj(a.s1,b.s1,a.s2),S=cj(a.s1,a.s2,b.s2);
	if (abs(s+S)<E) return p(19260817,19260817);
	s=s/(s+S);
	
	return p(b.s1.x+(b.s2.x-b.s1.x)*s,b.s1.y+(b.s2.y-b.s1.y)*s);
}
long double dis(p a,p b)
{
	return sqr(a.x-b.x)+sqr(a.y-b.y);
}
long double jl(P l,p x)
{
	long double s=dj(l.s1,l.s2,x),S=dis(l.s1,l.s2);
	if (abs(S)<E) return 0;
	return sqrt(dis(l.s1,x)-sqr(s)/S);
}

bool cmp(p a,p b)
{
	return a.s>b.s || a.s==b.s && b.x*a.y-a.x*b.y>0;
}
bool Cmp(P a,P b)
{
	long double s=b.S.x*a.S.y-a.S.x*b.S.y;
	return a.S.s>b.S.s || a.S.s==b.S.s && s>0 || a.S.s==b.S.s && abs(s)<E && a.Jl<b.Jl;
}

void xx(p &a) //xiangxian
{
	if (a.x>0 && !a.y ) a.s=1; else
	if (a.x>0 && a.y>0) a.s=2; else
	if (!a.x  && a.y>0) a.s=3; else
	if (a.x<0 && a.y>0) a.s=4; else
	if (a.x<0 && !a.y ) a.s=5; else
	if (a.x<0 && a.y<0) a.s=6; else
	if (!a.x  && a.y<0) a.s=7; else
	if (a.x>0 && a.y<0) a.s=8;
}

void add(p a,p b)
{
	++len;
	ans[len].s1=a;
	ans[len].s2=b;
	ans[len].Jl=jl(ans[len],O);
}

void work()
{
	int i,j,k,l;
	
	j=1;
	while (Cj(a[1],a[j%n+1])>0)
	j=j%n+1;
	
	fo(i,1,n)
	{
		while (Cj(a[i],a[j%n+1])>0)
		j=j%n+1;
		k=j%n+1;
		
		if (i!=j) add(a[i],a[j]);
		if (i!=k) add(a[i],a[k]);
	}
}

void Work()
{
	int i,j,k,l;
	p s;
	
	h=1;
	t=1;
	d[1]=1;
	
	fo(i,2,len)
	{
		while (h<t && cj(ans[i].s1,D[t-1],ans[i].s2)>=0) --t;
		while (h<t && cj(ans[i].s1,D[h]  ,ans[i].s2)>=0) ++h;
		
		s=jd(ans[i],ans[d[t]]);
		if (cj(ans[d[h]].s1,ans[d[h]].s2,s)>0 || h==t)
		{
			D[t]=s;
			d[++t]=i;
		}
	}
	
	while (h<t && cj(ans[d[t]].s1,D[h],ans[d[t]].s2)>=0) ++h;
	s=jd(ans[d[h]],ans[d[t]]);
	D[t]=s;
}

int main()
{
	freopen("everdream.in","r",stdin);
	freopen("everdream.out","w",stdout);
	
	O.x=0,O.y=0;
	for (NUM=getint(),T=getint();T;--T)
	{
		n=getint(),--n;
		
		X=getint(),Y=getint();
		fo(i,1,n)
		a[i].x=getint(),a[i].y=getint();
		
		fo(i,1,n)
		{
			a[i].x-=X,a[i].y-=Y;
			xx(a[i]);
			
			if (a[i].x)
			AA[i]=a[i].y/a[i].x;
			else
			AA[i]=19260817;
		}
		sort(AA+1,AA+n+1);
		
		j=0;
		fo(i,2,n)
		if (AA[i-1]==AA[i])
		{
			printf("0.0000000000\n");
			j=-1;
			break;
		}
		if (j) continue;
		
		sort(a+1,a+n+1,cmp);
		
		len=0;
		p _S1(inf-X,inf-Y),_S2(-inf-X,inf-Y),_S3(-inf-X,-inf-Y),_S4(inf-X,-inf-Y);
		add(_S1,_S4);add(_S4,_S3);add(_S3,_S2);add(_S2,_S1);
		
		fo(i,1,n-1)
		add(a[i],a[i+1]);
		add(a[n],a[1]);
		
		work();
		
		fo(i,1,len)
		{
			if (Cj(ans[i].s1,ans[i].s2)<0)
			{
				Swap=ans[i].s1;
				ans[i].s1=ans[i].s2;
				ans[i].s2=Swap;
			}
			ans[i].S.x=ans[i].s2.x-ans[i].s1.x;
			ans[i].S.y=ans[i].s2.y-ans[i].s1.y;
			
			xx(ans[i].S);
		}
		sort(ans+1,ans+len+1,Cmp);
		
		Len=0;
		fo(i,1,len)
		{
			if (i==1 || Cj(ans[i-1].S,ans[i].S))
			ans[++Len]=ans[i];
		}
		len=Len;
		
		Work();
		
		Ans=0;
		fo(i,h,t-1)
		Ans+=Cj(D[i],D[i+1]);
		Ans+=Cj(D[t],D[h]);
		printf("%0.10Lf\n",Ans/2);
	}
	
	fclose(stdin);
	fclose(stdout);
	
	return 0;
}