5821. 【NOIP提高A组模拟2018.8.16】 手机信号

题目描述

Input
第一行由一个空格隔开的两个正整数 m, c，意义见题目描述。
接下来 m 行，每行可能有以下形式：
construct l r v 代表发生了第一种事件；
destruct l r 代表发生了第二种事件；
query x 代表发生了第三种事件。
Output
对于每个 query 操作，请输出一行一个整数代表此时坐标 x 处的信号强度。

Sample Input
11 10000
query 5
construct 5 500 100
query 500
query 1000
construct 10 90 5
query 44
destruct 44 66
query 55
construct 50 60 3
query 46
query 6000
Sample Output
0
975
0
9999
9775
9984
0

Data Constraint

30%

暴力。。。

60%

线段树随便搞搞。。。
（话说比赛时居然没有人写）

---

题外话

题解使用set来维护，似乎也可以把询问挂在线段树上
然而我并不是这么做

比赛时就想到了这种方法之后成功写了一天

0%

考虑直接维护场上的基站情况
显然一个一个加的话还不如暴力

有一个很显(sha)然(bi)的方法，每次修改就把区间修改为本次修改的编号
删除就直接清0
询问可以在左右各二分出一次最靠近该点的修改，然后用一些奇♂妙的方法求出两端最近的基站位置

举个栗子

（相同颜色代表同一次修改，竖线代表基站）

二分会找到这里

但是可以发现，左边找到的不是一个基站，所以再求得该次修改中，在二分位置左边第一个基站

就是这样，右边同理

至于怎么奇♂妙地找到基站，设询问位置为x，找到的修改编号为Find，a[Find][0/1/2]分别代表询问的l/r/v（注意两边的Find可能不同）
那么
左边：min(((l-a[Find][0])/a[Find][2])*a[Find][2]+a[Find][0],a[Find][1])
右边：max(((l-a[Find][0]+a[Find][2]-1)/a[Find][2])*a[Find][2]+a[Find][0],a[Find][0])

基本思想就是找到当前所在的块，然后找到块的其中一段
注意有可能找到的位置超出了范围，所以要取max/min

---

其实这样做有问题
举个栗子

很显然，最优应该是往左边走
但是由于该位置被红色覆盖了，所以往左往右走都会走到红色上

所以，需要一些奇♂妙的方法来处理

30%

仔细想想锅出在哪里
因为区间不会重叠，所以如果当前段里只有本次修改那就没有问题

然而，就像上面的例子一样，如果当前段里还有其它段的话

就会发现当询问在边上的两段时，就无法考虑到蓝色段的影响

为了解决这个问题，必须要把旁边的两段清空（不然会错）
所以在实际操作中，修改一个区间时，应先把修改的区间所在块清空再修改（因为区间不会重叠，所以只可能在一个块中）

删除操作同理，但是因为删除的两个端点可能在不同的块中，所以要分别考虑（最多两个块）
（注意一下删除和询问的不同之处，如果删掉了一个基站那么要清掉基站连着的块）

演示一下：

修改

修改（+清空）

修改

删除

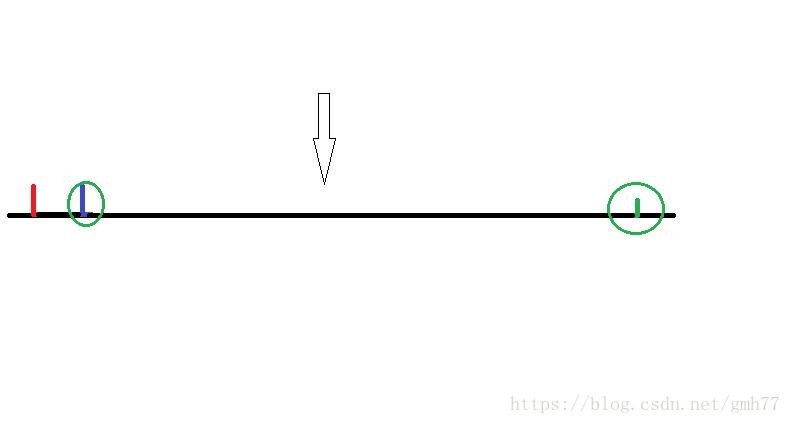
询问

就是这样，时间复杂度$O(n \log^2 n)$
比100%还难写所以不调了

100%

然而这样写第四个点线段树就炸了（动态开点）

考虑在线段树中多维护两个量，表示当前区间中非0的位置（最左/右）
然后直接询问，不用二分

没了。
时间复杂度$O(n \log n)$
但是常数大到*****
成功垫底
被pascal选手踩在脚下

code

码量十分清真

也就快300行5000byte而已

#include <iostream>
#include <cstdlib>
#include <cstdio>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define min(x,y) (x<y?x:y)
#define max(x,y) (x>y?x:y)
#define Len 1000000000
#define bj -233333333
using namespace std;

int a[200001][3];
int tr[20000001][6];
int n,m,i,j,k,l,r,mid,len,Find,x,y,z;
char s[15];
long long ans,c;

bool BZ;

void New(int t,int x)
{
    if (!tr[t][x])
    {
        tr[t][x]=++len;
        tr[len][3]=bj;
        tr[len][4]=-1;
        tr[len][5]=Len+1;
    }
}

void cg(int t,int l,int r)
{
    if (tr[t][3]!=bj)
    {
        if (tr[t][3])
        {
            tr[t][4]=r;
            tr[t][5]=l;
        }
        else
        {
            tr[t][4]=-1;
            tr[t][5]=Len+1;
        }
        tr[t][2]=tr[t][3];
    }
}

void down(int t,bool bz,int l,int r)
{
    if (tr[t][3]!=bj)
    {
        if (tr[t][3])
        {
            tr[t][4]=r;
            tr[t][5]=l;
        }
        else
        {
            tr[t][4]=-1;
            tr[t][5]=Len+1;
        }

        tr[t][2]=tr[t][3];

        if (bz)
        {
            tr[tr[t][0]][3]=tr[t][3];
            tr[tr[t][1]][3]=tr[t][3];
        }

        tr[t][3]=bj;
    }
}

void change(int t,int l,int r,int x,int y,int s)
{
    int mid=(l+r)/2;

    if (l<r)
    {
        New(t,0);
        New(t,1);
    }
    down(t,l<r,l,r);

    if (x<=l && r<=y)
    {
        tr[t][3]=s;
        down(t,l<r,l,r);

        return;
    }

    if (x<=mid)
    change(tr[t][0],l,mid,x,y,s);
    if (mid<y)
    change(tr[t][1],mid+1,r,x,y,s);

    if (l<r)
    {
        cg(tr[t][0],l,mid);
        cg(tr[t][1],mid+1,r);
    }

    tr[t][2]=max(tr[tr[t][0]][2],tr[tr[t][1]][2]);

    tr[t][4]=max(tr[tr[t][0]][4],tr[tr[t][1]][4]);
    tr[t][5]=min(tr[tr[t][0]][5],tr[tr[t][1]][5]);
}

void find(int t,int l,int r,int x,int y)
{
    int mid=(l+r)/2;

    if (l<r)
    {
        New(t,0);
        New(t,1);
    }
    down(t,l<r,l,r);

    if (l<r)
    {
        cg(tr[t][0],l,mid);
        cg(tr[t][1],mid+1,r);
    }

    if (x<=l && r<=y)
    {
        Find=max(Find,tr[t][2]);
        return;
    }

    if (x<=mid)
    find(tr[t][0],l,mid,x,y);

    if (Find) return;

    if (mid<y)
    find(tr[t][1],mid+1,r,x,y);
}

void find2(int t,int l,int r,int x,int y,bool type)
{
    int mid=(l+r)/2;

    if (l<r)
    {
        New(t,0);
        New(t,1);
    }
    down(t,l<r,l,r);

    if (l<r)
    {
        cg(tr[t][0],l,mid);
        cg(tr[t][1],mid+1,r);
    }

    if (x<=l && r<=y)
    {
        if (!type)
        Find=max(Find,tr[t][4]);
        else
        Find=min(Find,tr[t][5]);

        return;
    }

    if (x<=mid)
    find2(tr[t][0],l,mid,x,y,type);
    if (mid<y)
    find2(tr[t][1],mid+1,r,x,y,type);
}

int main()
{
    freopen("cellphone.in","r",stdin);
    freopen("cellphone.out","w",stdout);

    tr[0][3]=bj;
    tr[1][3]=bj;
    tr[0][4]=-1;
    tr[0][5]=Len+1;
    len=1;

    scanf("%d%lld",&n,&c);
    fo(i,1,n)
    {
        scanf("%s",s);

        switch (s[0])
        {
            case 'c':
                {
                    scanf("%d%d%d",&x,&y,&z);
                    y=((y-x)/z)*z+x;

                    m++;
                    a[m][0]=x;
                    a[m][1]=y;
                    a[m][2]=z;

                    Find=0;
                    find(1,0,Len,x,y);

                    if (Find)
                    {
                        l=((x-a[Find][0])/a[Find][2])*a[Find][2]+a[Find][0]+1;
                        r=((x-a[Find][0])/a[Find][2]+1)*a[Find][2]+a[Find][0]-1;

                        change(1,0,Len,l,r,0);
                    }
                    change(1,0,Len,x,y,m);

                    break;
                }

            case 'd':
                {
                    scanf("%d%d",&x,&y);

                    if (x)
                    {
                        Find=0;
                        find(1,0,Len,x-1,x-1);
                        if (Find)
                        l=((x-a[Find][0]-1)/a[Find][2])*a[Find][2]+a[Find][0]+1;
                        else
                        l=x;
                    }
                    if (y<Len)
                    {
                        Find=0;
                        find(1,0,Len,y+1,y+1);
                        if (Find && y>=a[Find][0])
                        r=((y-a[Find][0])/a[Find][2]+1)*a[Find][2]+a[Find][0]-1;
                        else
                        r=y;
                    }

                    change(1,0,Len,l,r,0);

                    break;
                }

            case 'q':
                {
                    ans=233333333;
                    ans*=10;

                    scanf("%d",&x);

                    if (!tr[1][2])
                    {
                        printf("0\n");
                        break;
                    }

                    Find=-1;
                    find2(1,0,Len,0,x,0);
                    l=Find;

                    if (l>-1)
                    {
                        Find=0;
                        find(1,0,Len,l,x);

                        if (Find)
                        ans=x-min(((l-a[Find][0])/a[Find][2])*a[Find][2]+a[Find][0],a[Find][1]);
                    }

                    Find=Len+1;
                    find2(1,0,Len,x,Len,1);
                    l=Find;

                    if (l<=Len)
                    {
                        Find=0;
                        find(1,0,Len,x,l);

                        if (Find)
                        ans=min(ans,max(((l-a[Find][0]+a[Find][2]-1)/a[Find][2])*a[Find][2]+a[Find][0],a[Find][0])-x);
                    }

                    printf("%lld\n",max(0,c-ans*ans));
                    break;
                }
        }
    }

    fclose(stdin);
    fclose(stdout);

    return 0;
}