贪心法——LeetCode 55 跳跃游戏

跳跃游戏

• 题目：

给定一个非负整数数组，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个位置。

示例 1:

输入: [2,3,1,1,4]
输出: true
解释: 我们可以先跳 1 步，从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。

示例 2:

输入: [3,2,1,0,4]
输出: false
解释: 无论怎样，你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 ， 所以你永远不可能到达最后一个位置。

---

• 思路分析

贪心法

1. 以题目为例 [2,3,1,1,4]，数组下标依次是a[0]=2,a[1]=3,a[3]=1…

那么第一个元素可以跳跃的步数为1步、2步，它可以跳1步到a[1]=3,a[3]之后可以跳1步、2步、3步，它可以跳3步直接到达数组尾部最后元素。

2. [3,2,1,0,4]，数组下标依次是a[0]=3，它可以跳跃的步数为1步、2步、3步，它跳3步到达a[4]=0,之后可以跳跃的步数为0，到不了数组最后一个元素。

3. 需要考虑的问题是从首元素开始，它可以跳跃的步数有很多种，应该选择哪一步呢？

4. 我们要选择跳跃的步数为最大的步数，因为最大步数可以覆盖小步数，也就是说经过小步数跳跃怎么都可以到达最大步数跳跃的位置。

5. 比如，元素a[0]要到达的最后位置是元素a[i]，它可以跳的位置为a[1] 、a[2]、a[3]…a[i-1]、a[i].

6. 若是此时不在第0个位置，在第i个位置，从该位置最远可以跳跃至第j个位置，第i个位置可以跳到的位置有第i+1、i+2…、j-1、j位置。

7. 我们要选择的能跳的位置就是这些位置中所在元素最大可以跳跃的步数，可以跳跃到最远的位置

8. 若是后面元素的步数越小，则保持最大的步数，直到后面有步数大于当前步数再去更新它。

步骤：

1. 从第i位置最远可跳跃到第a[i]位置，从第i位置最远可跳跃nums[i]步，所以a[i]=nums[i]+1

2. 设iump当前所在位置为0

3. 设max_[a]:从第0位置到第jump位置过程中最远可到达的位置，初值为max_a[0]

4. 用jump扫描a数组，直到jump到达数组的尾部或jump超过max_a,更新max_a(也就是更新最大的步数)

5. jump:若jump为数组长度，返回true，反之，false

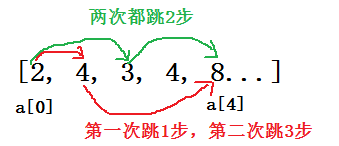
例：a=[2,4,3,4,8,6…]

之后依次类推，不断更新，直到数组尾部

• C++代码：

class Solution {
public:
    bool canJump(vector<int>& nums) {
        std::vector<int> a;  //最远可跳跃位置
        for(int i=0;i<nums.size();i++){
             a.push_back(i+nums[i]);
        }
       int jump=0;
       int max_a=a[0];
       while(jump<a.size()&&jump<=max_a){ //步数不能超过数组长度且步数不能超过当前最远位置
           if(max_a<a[jump]){
               max_a=a[jump];
           }
           jump++;
       }
       if(jump==a.size()){  //jump到数组尾部
           return true;
       }
       return false;
    }
};