数据结构-图

目录

0,感谢

 在学习过程中感谢各位博客大神的无私奉献，让我这个初学者受益匪浅，特此感谢，博客大部分只是作为学习笔记，如有差错，敬请指正！
[1]数据结构—图的详细介绍

1,图

1.1,名词解释

图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成，表示为G(V,E):G表示一个图，V是图G中顶点的集合，E是图G中边的集合。
图中的数据元素，称之为顶点(Vertex),顶点集合有穷非空。
图中的两个顶点之间都有可能有关系，顶点之间的逻辑关系用边来表示，边集可以是空的。

1.1.1,无向图，有向图

按照边的有无方向分为无向图和有向图。

无向图: 顶点+边
有向图: 顶点+弧(弧有弧头，弧尾，箭头一端为弧头)

1.1.2,稀疏图，稠密图

按照边或弧的多少进行区分

完全图： 任意两顶点之间都存在边
有向完全图： 完全图有向
简单图： 若无重复的边或顶点到自身的边

1.1.3,邻接点，依附

度： 无向图顶点的边数
出度，入度： 有向图的弧

1.1.4,网，环，简单路径，连通图，强连通图，连通分量，强连通分量

网： 图上的边或弧带有权
环： 两点间存在路径，则说明两点联通，路径最终回到起始点
简单路径： 不重复的路径
连通图： 任意两点连通
强连通图： 有向连通图
连通分量： 子图极大联通
强连通分量： 有向联通分量

1.1.5,生成树，有向树

生成树： 无向图中连通且n个顶点n-1条边
有向树： 有向图中一顶点的入度为0其余顶点入度为1
生成森林： 一个有向图由若干有向树构成

1.2,图的存储结构—邻接矩阵

包含两个数组
一维数组：每个数据元素的信息
二维数组：表示图中的边或者弧信息

无向图：

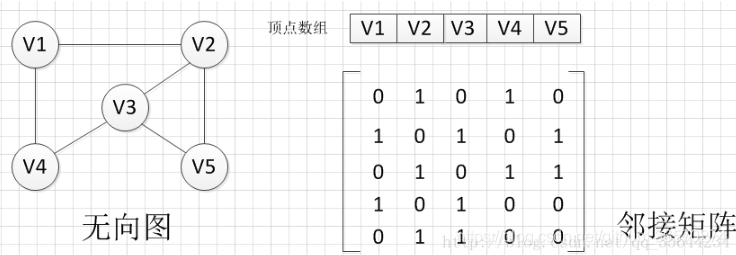
1，无向图是根据对角线对称
2，某个顶点的度 =对应行/列的元素之和
有向图

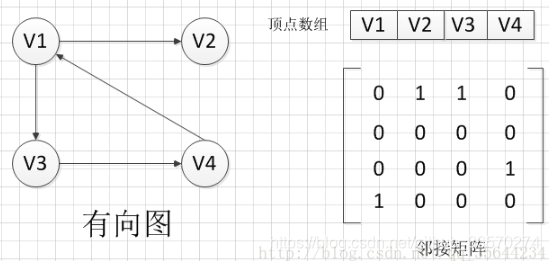
1，出度： 行之和；入度： 列之和

1.2.1,邻接矩形表示代码

//不同类型枚举
enum Graphkind
{
   
   
	DG, //有向图
	DN, //无向图
	UDG,//有向网
	UDN //无向网
};

//节点类
typedef struct Node
{
   
   
	int *vex;//顶点数组
	int vexnum;//顶点个数
	int edge;//边个数
	int ** adjMatrix;//邻接矩形
	Graphkind kind;
}MGraph;

//创建邻接矩形
void createGraph(MGraph &G,Graphkind kind)
{
   
   
	cout << "输入顶点的个数" << endl;
	cin >> G.vexnum;
	cout << "输入边的个数" << endl;
	cin >> G.edge;

	//枚举
	G.kind = kind;

	//为两个数组开辟空间
	G.vex = new int[G.vexnum];
	G.adjMatrix = new int*[G.vexnum];//指针数组

	int i;

	for (i =0;i < G.vexnum;i++)
	{
   
   
		G.adjMatrix[i] = new int[G.vexnum];
	}//生成邻接矩阵

	//遍历邻接矩阵,将整个邻接矩阵初始化为0或∞
	for (i =0;i<G.vexnum;i++)
	{
   
   
		for (int k=0;k<G.vexnum;k++)
		{
   
   
			if (G.kind == DG || G.kind == DN)
			{
   
   
				G.adjMatrix[i][k] = 0;
			}
			else
				G.adjMatrix[i][k] = INT_MAX;
		}
	}

	cout << "请输入两个有关系的顶点的序号：例如：1 2 代表1号顶点指向2号顶点" << endl;
	for (i =0;i<G.edge;i++)
	{
   
   
		int a, b;
		cin >> a;
		cin >> b;

		if (G.kind == DN)//无向图
		{
   
   
			G.adjMatrix[b - 1][a - 1] = 1;
			G.adjMatrix[a - 1][b - 1] = 1