一种用于全局优化和模拟电路设计自动化的WOA与mGWO算法混合方法
目标
–本文旨在通过使用所提出的元启发式优化算法来解决模拟电路设计中的尺寸设计问题。
设计/方法/途径
–提出了一种鲸鱼优化算法与改进的灰狼优化算法的混合算法(WOA‐mGWO),并将其应用于模拟电路的自动化设计。
研究结果
–所提出的混合WOA‐mGWO算法在23个经典基准函数上的测试中,在收敛速度和函数的平均适应度方面表现出更优的性能。此外,通过20次独立运行并结合威尔科克森秩和检验进行了严格的性能评估。
实际意义
–为了评估所提出算法的性能,采用了一个传统的两级运算放大器。通过在MATLAB中仿真该算法计算出宽长比,随后使用180纳米CMOS标准工艺在Cadence环境中设计运算放大器。
原创性/价值
–混合WOA‐mGWO算法通过结合两种元启发式算法——鲸鱼优化算法和改进的灰狼优化算法的能力,旨在提升算法的探索能力。为进一步建立可信度并证明该算法在当前先进科学技术中的重要意义,还进行了20次独立运行的统计研究,以验证所提出算法的鲁棒性,得到模拟集成电路尺寸设计问题的最优、平均和最差解。本文还提供了与其他重要尺寸设计工具的最优解比较,证明了混合WOA‐mGWO算法的有效性。同时进行了蒙特卡洛仿真和工艺角分析,以验证设计的稳定性。
关键词
优化设计,计算机辅助设计,设计优化方法
论文类型
研究论文
1 引言
近年来,半导体产业的出货量快速增长,从1978年的32.6亿台设备增长到2017年的约1.0751万亿台设备(McClean,2018)。根据世界半导体贸易统计公司( WSTS)的数据,2017年全球市场增长率达到创纪录的21.6%,市场规模达4122亿美元,并预计在2018年保持相同水平(WSTS,2017)。尽管模拟电路在整个集成电路中所占比例较小,但其设计相比数字电路更为复杂且耗时,从而延长了整体上市时间。该设计流程需要高度熟练的设计者,使其成为集成电路设计流程中的主要瓶颈之一。
模拟电路设计
收稿日期 2018年4月27 日,修订日期 2018年8月13 日、2018年10月26日,录用日期 2018年10月29日
COMPEL ‐ 电气与电子工程计算与数学国际期刊 © Emerald出版有限公司 0332‐1649 DOI 1.108/COMPEL-04-2018-0175
该期刊的当前期和全文档案可在Emerald Insight上获取:www.emeraldinsight.com/0332-1649.htm
任何电路设计过程都必须经历三个阶段,即选择相关的应用特定候选拓扑结构,然后获取电路参数,最后将其转化为版图(fi)。由于获得最优设计参数的过程依赖于具体规格和电路性能,因此这一过程相当重要。为了在提高设计精度的同时缩短设计时间,需要采用迭代计算技术。本文重点研究电路设计的第二阶段,即电路尺寸设计,考虑到其对整个设计流程的影响,并假设拓扑结构已由设计者选定。
fiGielen和Sansen,1991)。整个获得最优设计参数的过程因其对规格和电路性能的依赖而显得尤为重要。为通过同时提高设计精度来减少设计时间,需要采用迭代计算技术。本文聚焦于电路设计的第二阶段,即电路尺寸设计,考虑其对整个设计流程的影响,假设拓扑结构已由设计者选定。
经典模拟电路设计流程包括综合与优化。综合阶段可分为基于知识、基于方程、基于仿真和基于建模的方法。在基于知识的方法中,如图1(a)所示,由设计者创建设计计划;而其他方法则侧重于优化过程而非设计计划。因此,基于方程、基于仿真和基于建模的方法均属于基于优化的方法,如图1(b)所示。尽管基于优化的方法因迭代导致计算时间较长,但由于其具有设置时间短、精度高等优势,因而优于基于知识的方法。然而,随着高速处理器的发展,模拟电路尺寸设计的计算时间仍处于可接受范围内(贾法里,2011)。
在优化阶段,优化技术用于精细调整从综合得到的初始解,因为该解可能并非最优解。优化技术分为确定性优化技术和元启发式优化技术。确定性优化技术也已应用于模拟电路的优化设计,采用改进的传统优化策略(泽姆利阿克,2014),使用确定性或随机方法。然而,这些方法存在局部最小值停滞、对目标函数的连续性和可微性的依赖,以及需要一个良好的起始点等缺陷(德巴希安和梅曼迪‐内贾德,2017b)。与确定性方法相比,一类基于种群的元启发式算法——群体智能算法,因其强健性、易于实现以及高灵活性,特别是在模拟电路尺寸设计工具的开发中,受到了广泛关注。图2 展示了用于模拟电路尺寸设计工具中优化部分的元启发式算法的分类。
近年来,研究努力致力于开发模拟集成电路尺寸设计工具,包括商业Solido(2018)和MunEDA(2018)以及学术类工具(例如AIDA,AIDAsoft,2018)。然而,电路尺寸设计工具的目标是提供尽可能最优的解,以在精度、运行时间和鲁棒性之间实现更好的权衡。因此,这些工具所提供的解不能被认为是尽可能最优的解。本文提出了一种结合鲸鱼优化算法(WOA)(米尔贾利和刘易斯,2016)与改进灰狼优化(mGWO)(Mittal 等,2016)算法综合能力的混合型工具,用于模拟电路的自动尺寸设计。在文献中,已开发出多种元启发式算法用于模拟电路尺寸设计问题。然而,据作者所知,这是首次将结合WOA和mGWO算法的混合模型应用于模拟集成电路尺寸设计。
本文的其余部分组织如下:第2节详细介绍了混合WOA‐mGWO算法。第3节通过对23个经典基准函数进行比较研究,评估了混合WOA‐mGWO算法。第4节介绍了通过构建成本函数将混合WOA‐mGWO应用于集成电路设计的流程。第5节提供了仿真结果,并与其他电路尺寸设计工具进行了比较,同时给出了统计研究结果。最后,第6节得出了结论。
2. 混合鲸鱼优化算法和改进的灰狼优化算法
WOA 和 mGWO 是分别受座头鲸和灰狼的社会等级及觅食或捕猎行为启发的元启发式算法。座头鲸和灰狼社会行为的数学建模是如(Sarkar等,2018)和(Mittal等,2016)所述。在混合WOA‐mGWO中,采用标准的WOA算法对整个搜索空间进行全局搜索,并将大多数解引导至有利区域。在探索阶段之后,使用mGWO算法在局部搜索最优解。在混合WOA‐mGWO中,WOA算法强调在搜索起始点处的扩展,以广泛探索整个搜索空间,而mGWO算法则通过允许搜索代理向最优解移动,专注于优化过程下一阶段的放大。该方法有效利用了两种算法的能力,充分应对局部和全局搜索过程。
2.1 所提出的混合鲸鱼优化算法和改进的灰狼优化算法的步骤
本节讨论所提出的混合WOA的详细流程 -mGWO算法 .
步骤1
:将种群规模N、维度D的随机向量初始化为优化算法的起始点。
$$Xi;j5lbj + rand\left(\right) ubj lbj$$
(1)
其中,Xi,j 是第i个解在第j维的位置;ubj 和 lbj 是第j维的上下界。此处,i 和 j 分别从 1 到 N 和 1 到 D 变化;rand()取 0 到 1 之间的任意随机数。
步骤2 :使用每个向量Xi,j评估适应度函数,即使用Xi,j计算整个种群的函数值,并获得最佳位置。
步骤3 :初始化算法参数,如r1;r2;A;C;a、b和p。变量r1,、r2和p取0到 1之间的随机值。系数向量A和C分别通过公式(2)和(3)获得。参数b是定义座头鲸对数螺旋的常数。a的分量按方程(4)所示计算,其值随着迭代从2递减至0。图3展示了在500次迭代过程中不同r值(即r = 1至6)下a的变化情况,有助于确定r的值,以略微增加分配给探索的迭代次数。换句话说,随着r的值增加,非线性程度增加,从而提升算法的整体探索能力。为了保持探索与开发之间的适当比例,Mittal等人在mGWO算法中选择r的值为2。

A = 2 a r1 a
(2)
C = 2 r2
(3)
a = 2 1
$$t$$r
Maxiter $$r$$
!
(4)
其中,r1和r2是范围[0,1],内的随机数,“.”表示逐元素相乘,t为当前迭代次数,Maxiter为最大迭代次数。
步骤4
:当 p< 0.5 且 A < 1 时,搜索代理的位置根据三个最优搜索代理(即 alpha、beta 和 delta)进行更新,如方程 (6a)、(6b)和(6c)所示,它们分别用 Xa;X b和 X d 表示。换句话说,其余的搜索代理依赖于这些最佳搜索代理,围绕猎物随机更新其位置。
Da = jC1 X a X j;
(5a)
Db = jC2 X b X j;
(5b)
Dd = jC3 X d X j
(5c)
X 1 = X a A1 Da ;
(6a)
X 2 = X b A2 Db ;
(6b)
X 3 = X d A3 Dd
(6c)
X t + 1 $$ = X 1 + X 2 + X 3
3
(7)
其中,X 表示搜索代理的当前位置,X t + 1 $$ 是相对于三个最优搜索代理的更新位置。
步骤5
:当 p < 0.5 且 A 1 时,通过随机选择的搜索代理,利用以下方程进行位置更新以实现探索。
D = jC X r X j
(8)
X t + 1 $$ = Xp A D
(9)
这里,X rt$$ 是从种群中随机选择的搜索代理的位置,Xp t$$ 表示猎物的位置向量。X t$$ 和 X t + 1 Þ 分别表示搜索代理的当前位置和更新后的位置。
步骤6
:当 p 0.5 时,搜索代理的位置根据三个最优搜索代理进行更新,如下所示。
Da = jC1 X a X j;
(10a)
Db = jC2 X b X j;
(10b)
Dd = jC3 X d X j
(10c)
X 1 = Da ebl cos 2pl $$+ Xa ð t$$;
(11a)
X 2 = Db ebl cos 2pl $$+ Xb ð t$$;
(11b)
X 3 = Dd ebl cos 2pl $$+ Xd ð t$$
(11c)
其中,l 是范围 [‐1, 1],X 1 内的随机数;X2 和 X3 表示搜索代理(即座头鲸)所观察到的螺旋形运动,位置更新基于三个最优搜索代理,如下所示:
X t + 1 $$ = X 1 + X 2 + X 3
3
(12)
步骤7 :如果任何控制变量超出限制,则将其值设置为下限或上限。
步骤8 :检查终止条件,即算法是否已运行指定的最大迭代次数。
步骤9 :若未满足终止条件,则返回步骤3。否则,输出获得的最优解。
优化流程的WOA‐mGWO算法可以用流程图的形式更好地说明,如图4所示。
3. 混合鲸鱼优化算法与改进灰狼优化算法的性能评估
混合WOA的性能 -将mGWO与其他算法在23个经典且流行的基准函数上进行比较(内纳瓦特和库马尔·贾托思,2017),如表I所示,以分析所提出算法的效率。这些基准函数被分类为单峰、固定低维以及多峰高维基准函数。通过对上述基准函数进行20次独立运行后的仿真结果,将所提出的混合WOA‐mGWO与其他算法(包括正弦余弦算法(SCA)(Mirjalili,2016)、鲸鱼优化算法(WOA)、粒子群优化(PSO)( Kennedy 和 Eberhart,1995)、灰狼优化(GWO)(Mirjalili等,2014)、改进型GWO(mGWO)以及引力搜索算法(GSA)与粒子群优化算法的混合( GSAPSO)(Mirjalili 和 Hashim,2010))进行比较。表II 列出了各算法在最终23个基准函数的迭代。这些函数的验证表明,混合WOA‐mGWO算法在23个基准函数中的15个上优于其他算法。
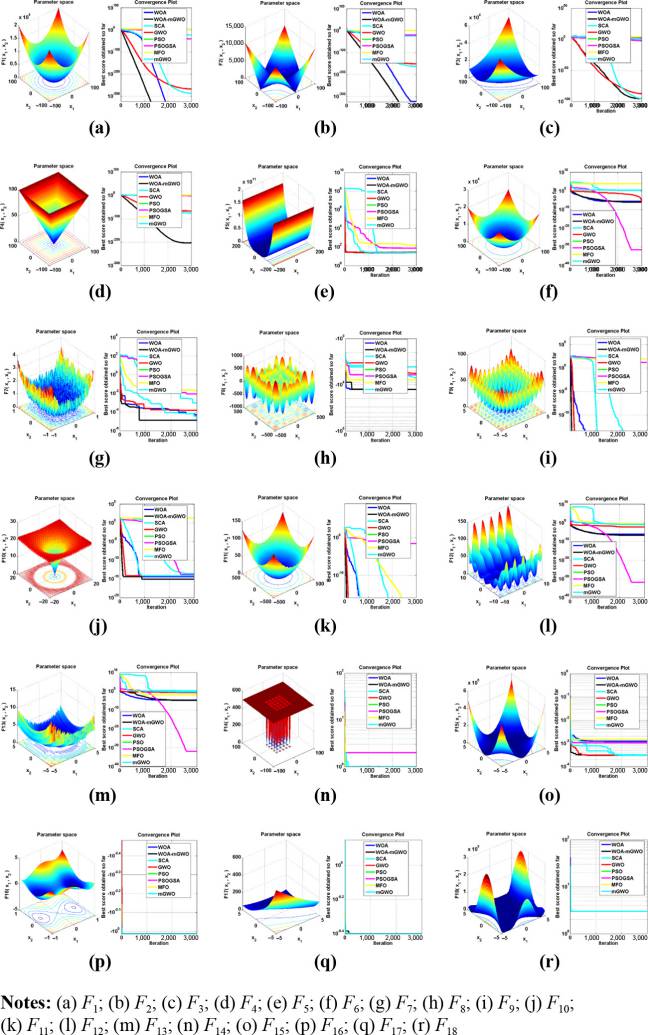
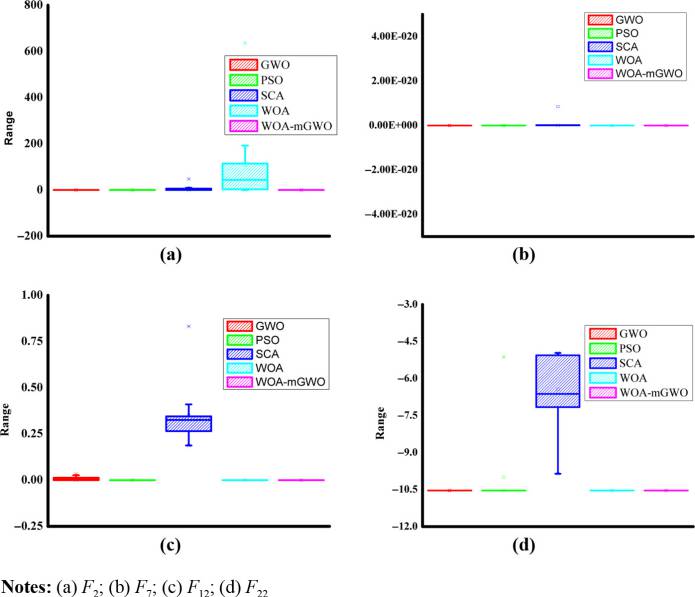
函数 F1 –F18和 F19 –F23使用GWO、SCA、WOA、PSO、GWO、GSAPSO、 MFO和WOA‐mGWO算法的收敛速度已进行了研究,如 图5 和 6 所示。随着迭代过程中的下降趋势,证明了混合WOA‐mGWO算法在获得更优的全局最优解收敛能力方面的优势。图7 展示了通过20次独立运行所提出的算法得到的结果的箱线图,并与GWO、SCA、WOA和PSO等其他算法在部分基准函数(即 F1,、3, F12和 F22) 上的表现进行了比较。收敛速度被用作验证所提出算法收敛性的指标。 表II 中的收敛图结果表明,混合WOA‐mGWO在多峰函数上具有更优的收敛速度,同时能够避免陷入局部最小值,展现出更高的效率。因此,混合WOA‐mGWO通过在探索与开发之间保持适当的平衡,被证实更适用于解决各类优化问题。
基于20次独立运行中的最佳、平均、最差和标准差值对算法进行比较时,无法针对每次单独的运行进行比较。因此,即使在20次运行中概率较低,仍有可能偶然出现优势情况。因此,进一步采用Wilcoxon统计进行分析
| Function | Formulation | D | Range | fmin |
|---|---|---|---|---|
| Sphere | $f_1(x) = \sum_{i=1}^{D} x_i^2$ | 30 | [–100, 100] | 0 |
| Schwefel 2.22 | $f_2(x) = \sum_{i=1}^{D} | x_i | + \prod_{i=1}^{D} | x_i |
| Schwefel 1.2 | $f_3(x) = \sum_{i=1}^{D} (\sum_{j=1}^{i} x_j^2)$ | 30 | [–100, 100] | 0 |
| Schwefel 2.21 | $f_4(x) = \max_i | x_i | ; 1 \leq i \leq D$ | 30 |
| Rosenbrock | $f_5(x) = \sum_{i=1}^{D-1} [100(x_{i+1} - x_i^2)^2 + (x_i - 1)^2]$ | 30 | [–30, 30] | 0 |
| Step | $f_6(x) = \sum_{i=1}^{D} (x_i + 0.5)^2$ | 30 | [–100, 100] | 0 |
| Quartic | $f_7(x) = \sum_{i=1}^{D} i x_i^4 + \text{random}[0, 1)$ | 30 | [–1.28, 1.28] | 0 |
| Schwefel | $f_8(x) = \sum_{i=1}^{D} x_i \sin(\sqrt{ | x_i | })$ | 30 |
| Rastrigin | $f_9(x) = 10D + \sum_{i=1}^{D} (x_i^2 - 10 \cos(2\pi x_i))$ | 30 | [–5.12, 5.12] | 0 |
| Ackley | $f_{10}(x) = -20 \exp(-0.2 \sqrt{\frac{1}{D} \sum_{i=1}^{D} x_i^2}) - \exp(\frac{1}{D} \sum_{i=1}^{D} \cos(2\pi x_i)) + 20 + e$ | 30 | [–32, 32] | 0 |
| Griewank | $f_{11}(x) = \frac{1}{4000} \sum_{i=1}^{D} x_i^2 - \prod_{i=1}^{D} \cos(\frac{x_i}{\sqrt{i}}) + 1$ | 30 | [–600, 600] | 0 |
(续)
| Function | Formulation | D | Range | fmin |
|---|---|---|---|---|
| Penalized | $f_{12}(x) = 0.1 [\sin^2(3\pi x_1) + \sum_{i=1}^{D-1} (x_i - 1)^2 (1 + \sin^2(3\pi x_{i+1})) + (x_n - 1)^2 (1 + \sin^2(2\pi x_n))] + \sum_{i=1}^{D} u(x_i, 10, 100, 4)$ where $y_i = 1 + \frac{x_i + 1}{4}$, and $u(x_i, a, k, m) = \begin{cases} k(x_i - a)^m, & x_i > a \ 0, & -a < x_i < a \ k(-x_i - a)^m, & x_i < -a \end{cases}$ | 30 | [–50, 50] | 0 |
| Penalized 2 | $f_{13}(x) = 0.1 [\sin^2(3\pi x_1) + \sum_{i=1}^{D-1} (x_i - 1)^2 (1 + \sin^2(3\pi x_{i+1})) + (x_n - 1)^2 (1 + \sin^2(2\pi x_n))] + \sum_{i=1}^{D} u(x_i, 5, 100, 4)$ | 30 | [–50, 50] | 0 |
| Foxholes | $f_{14}(x) = \left( \frac{1}{500} + \sum_{j=1}^{25} \frac{1}{j + \sum_{i=1}^{D} (x_i - a_{ij})^6} \right)^{-1}$ | 2 | [–65.536, 65.536] | 0.998004 |
| Kowalik | $f_{15}(x) = \sum_{i=1}^{11} \left( a_i - \frac{x_1 (b_i^2 + b_i x_2)}{b_i^2 + b_i x_3 + x_4} \right)^2$ | 4 | [–5, 5] | 0.000307 |
| Six-hump Camel-Back | $f_{16}(x) = 4x_1^2 - 2.1x_1^4 + \frac{1}{3}x_1^6 + x_1 x_2 - 4x_2^2 + 4x_2^4$ | 2 | [–5, 5] | –1.03162 |
| Branin | $f_{17}(x) = \left( x_2 - \frac{5.1}{4\pi^2} x_1^2 + \frac{5}{\pi} x_1 - 6 \right)^2 + 10 \left( 1 - \frac{1}{8\pi} \right) \cos x_1 + 10$ | 2 | [–5,5] | 0.398 |
| Goldstein-Price | $f_{18}(x) = [1 + (x_1 + x_2 + 1)^2 (10 - 14x_1 + 3x_1^2 - 14x_2 + 6x_1 x_2 + 3x_2^2)] \times [30 + (2x_1 - 3x_2)^2 (18 - 32x_1 + 12x_1^2 + 48x_2 - 36x_1 x_2 + 27x_2^2)]$ | 2 | [–5,5] | 3 |
(续)
| Function | Formulation | D | Range | fmin |
|---|---|---|---|---|
| Hartman 3 | $f_{19}(x) = -\sum_{i=1}^{4} c_i \exp \left( -\sum_{j=1}^{3} a_{ij} (x_j - p_{ij})^2 \right)$ | 3 | [–5,5] | –3.86278 |
| Hartman 6 | $f_{20}(x) = -\sum_{i=1}^{4} c_i \exp \left( -\sum_{j=1}^{6} a_{ij} (x_j - p_{ij})^2 \right)$ | 6 | [–5, 5] | –3.32236 |
| Shekel5 | $f_{21}(x) = -\sum_{i=1}^{5} [(x - a_i)(x - a_i)^T + c_i]^{-1}$ | 3 | [–5, 5] | –10.1532 |
| Shekel7 | $f_{22}(x) = -\sum_{i=1}^{7} [(x - a_i)(x - a_i)^T + c_i]^{-1}$ | 3 | [–5, 5] | –10.4029 |
| Shekel10 | $f_{23}(x) = -\sum_{i=1}^{10} [(x - a_i)(x - a_i)^T + c_i]^{-1}$ | 3 | [–5, 5] | –10.5364 |
表 I. 实验研究中使用的基准函数(D:维度,fmin:全局最小值)
| SCA | WOA | PSO | GWO | mGWO | GSA PSO | WOA-mGWO | |
|---|---|---|---|---|---|---|---|
| MF1 | 1.54E-19 | 0 | 1.80E-37 | 1.40E-263 | 1.77E-203 | 1.53E-19 | 0 |
| B | 7.18E-28 | 0 | 2.30E-50 | 8.94E-269 | 3.40E-210 | 1.03E-19 | 0 |
| W | 3.01E-18 | 0 | 3.32E-36 | 1.25E-262 | 3.32E-202 | 2.11E-19 | 0 |
| SD | 1.85E-19 | 0 | 7.33E-37 | 0 | 0 | 2.76E-20 | 0 |
| F2 | |||||||
| M | 9.07E-22 | 2.03E-322 | 2.88E-20 | 9.09E-150 | 7.04E-119 | 1.61E-09 | 0 |
| B | 2.08E-26 | 1.40E-322 | 1.25E-24 | 7.65E-153 | 5.12E-121 | 1.43E-09 | 0 |
| W | 6.19E-21 | 2.80E-322 | 2.78E-19 | 1.30E-148 | 3.82E-118 | 1.90E-09 | 0 |
| SD | 1.10E-19 | 0 | 5.88E-18 | 9.86E-150 | 8.6E-162 | 1.27E-10 | 0 |
| F3 | |||||||
| M | 64.6287 | 72.4 | 0.0116 | 7.18E-79 | 1.33E-52 | 833.33 | 1.23E-87 |
| B | 0.0004 | 0.5546 | 0.0028 | 2.16E-97 | 3.20E-66 | 7.93E-19 | 5.3E-142 |
| W | 836.82 | 353.3114 | 0.0358 | 1.44E-77 | 1.59E-51 | 6666.66 | 1.67E-86 |
| SD | 68.0306 | 164.3779 | 0.0089 | 8.90E-85 | 2.64E-88 | 2059.06 | 2.75E-85 |
| F4 | |||||||
| M | 0.3390 | 15.3559 | 0.0105 | 4.20E-66 | 3.84E-53 | 8.2791 | 9.3E-196 |
| B | 0.00019 | 3.93E-19 | 0.0023 | 4.81E-69 | 2.97E-56 | 1.70E-10 | 4.3E-207 |
| W | 3.1836 | 80.7672 | 0.0389 | 4.83E-65 | 2.77E-52 | 82.1799 | 1.8E-194 |
| SD | 0.4404 | 19.4109 | 0.0055 | 6.13E-66 | 1.51E-77 | 24.952 | 0 |
| F5 | |||||||
| M | 94.8308 | 24.3639 | 4.75E+01 | 25.9161 | 26.7851 | 20.492 | 24.3451 |
| B | 26.6304 | 24.0293 | 1.53E+01 | 24.3029 | 26.1738 | 4.1395 | 23.8722 |
| W | 1378.96 | 24.9405 | 8.74E+01 | 27.0720 | 28.5489 | 73.777 | 26.9609 |
| SD | 0.6309 | 0.2106 | 2.78E+01 | 0.6472 | 0.7516 | 13.093 | 0.2660 |
| F6 | |||||||
| M | 3.5692 | 6.06E-06 | 1.96E-32 | 0.1628 | 0.6141 | 505.0125 | 7.43E-07 |
| B | 2.6355 | 2.90E-06 | 0 | 4.28E-07 | 0.2502 | 1.18E-19 | 2.88E-07 |
| W | 4.0905 | 1.27E-05 | 6.78E-32 | 0.5030 | 1.4991 | 10100.25 | 1.18E-06 |
| SD | 0.3552 | 4.07503 | 2.60E-32 | 0.228 | 0.4033 | 2258.48 | 5.59E-02 |
(续)
表 II. 23个基准函数在20次独立运行中的最小化结果,针对F1‐F23
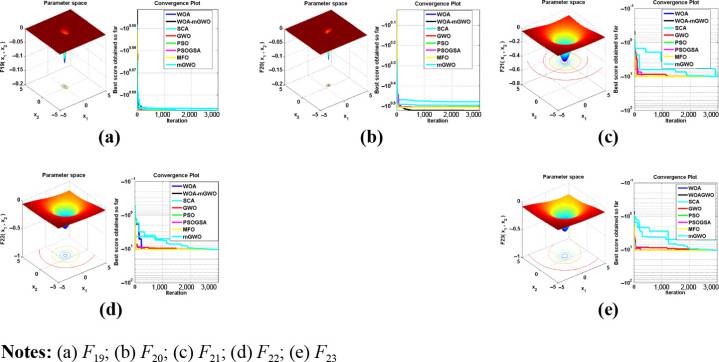
 比较的 下降趋势的 GWO, PSO, SCA, WOA, MFO, PSOGSA和WOA‐ mGWO)
比较的 下降趋势的 GWO, PSO, SCA, WOA, MFO, PSOGSA和WOA‐ mGWO)
| SCA | WOA | PSO | GWO | mGWO | GSA PSO | WOA-mGWO | |
|---|---|---|---|---|---|---|---|
| F7 | |||||||
| M | 0.0035 | 1.49E-04 | 8.77E-03 | 0.0001 | 3.23E-04 | 0.00906 | 6.71E-05 |
| B | 0.0002 | 6.14E-06 | 4.84E-03 | 7.83E-06 | 1.07E-04 | 0.0033 | 3.08E-06 |
| W | 0.0294 | 5.77E-04 | 1.46E-02 | 0.0004 | 7.57E-04 | 0.0184 | 1.45E-04 |
| SD | 0.004 | 2.6E-04 | 3.17E-03 | 4.61E-05 | 2.56E-05 | 0.0039 | 4.21E-05 |
| F8 | |||||||
| M | –4363.6 | –11958.18 | –6855.10 | –6282.65 | –5705.05 | –8401.25 | –12011.81 |
| B | –5061.8 | –12569.48 | –8798.60 | –7639.64 | –6501.72 | –9441.42 | –12569.48 |
| W | –4034.8 | –8569.20 | –5462.02 | –5288.60 | –4901.58 | –7195.47 | –8739.81 |
| SD | 235.92 | 306.89 | 620.75 | 425.84 | 1446.42 | 723.46 | 820.85 |
| F9 | |||||||
| M | 1.991 | 0 | 23.5307 | 0 | 0 | 105.11 | 0 |
| B | 0 | 0 | 16.9142 | 0 | 0 | 47.757 | 0 |
| W | 38.86 | 0 | 38.8033 | 0 | 0 | 142.27 | 0 |
| SD | 0.925 | 0 | 4.9232 | 0 | 0 | 24.787 | 0 |
| F10 | |||||||
| M | 11.375 | 3.73E-15 | 1.14E-14 | 7.82E-15 | 7.82E-15 | 1.8604 | 3.20E-15 |
| B | 7.99E-15 | 8.88E-16 | 7.99E-15 | 4.44E-15 | 4.44E-15 | 2.32E-10 | 8.88E-16 |
| W | 20.1743 | 4.44E-15 | 1.51E-14 | 7.99E-15 | 7.99E-15 | 19.0521 | 4.44E-15 |
| SD | 9.187 | 2.15E-15 | 3.51E-15 | 1.81E-15 | 1.79E-15 | 5.7282 | 1.67E-15 |
| F11 | |||||||
| M | 6.43E-08 | 0 | 0.0116 | 0 | 1.29E-03 | 0.00959 | 0 |
| B | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| W | 1.06E-06 | 0 | 0.0320 | 0 | 1.3E-03 | 0.04658 | 0 |
| SD | 0.018 | 4.1E-03 | 0.0138 | 0 | 0 | 0.01186 | 0 |
| F12 | |||||||
| M | 0.3185 | 9.56E-07 | 1.68E-32 | 0.0132 | 0.0502 | 0.8102 | 0.0016 |
| B | 0.200 | 5.19E-07 | 1.58E-32 | 0.0011 | 0.0196 | 1.29E-21 | 7.40E-08 |
| W | 0.4102 | 1.86E-06 | 2.12E-32 | 0.0337 | 0.1434 | 1.9775 | 0.0065 |
| SD | 0.0468 | 4.14E-07 | 6.20E-34 | 0.0107 | 0.05115 | 0.65774 | 0.0023 |
| F13 | |||||||
| M | 2.0002 | 5.6E-04 | 5.49E-04 | 0.1557 | 0.5299 | 0.00054 | 0.0235 |
| B | 1.798 | 3.35E-06 | 1.47E-32 | 7.60E-07 | 0.1983 | 2.02E-20 | 2.13E-06 |
| W | 2.1918 | 0.0109 | 1.10E-02 | 0.4757 | 0.8295 | 0.01098 | 0.2479 |
| SD | 0.227 | 3.19E-05 | 1.16E-31 | 0.1208 | 0.1473 | 0.00245 | 0.0538 |
| F14 | |||||||
| M | 0.998 | 0.998 | 1.2962 | 2.1806 | 4.2252 | 1.0477 | 0.998 |
| B | 0.998 | 0.998 | 0.9980 | 0.9980 | 0.9980 | 0.998 | 0.998 |
| W | 0.998 | 0.998 | 1.9920 | 10.763 | 12.6705 | 1.9920 | 0.998 |
| SD | 2.2241 | 0.3059 | 5.23E-07 | 2.69E-14 | 2.2353 | 0.22227 | 2.24E-14 |
| F15 | |||||||
| M | 0.0006 | 5.87E-04 | 4.87E-04 | 0.0033 | 0.0044 | 0.00436 | 3.19E-04 |
| B | 0.0003 | 3.1E-04 | 3.07E-04 | 0.0003 | 0.0003 | 0.00030 | 3.07E-04 |
| W | 0.0012 | 1.22E-03 | 1.05E-3 | 0.0203 | 0.0203 | 0.02036 | 5.16E-04 |
| SD | 0.00035 | 2.9E-04 | 3.35E-04 | 0.0061 | 9.21E-10 | 0.008209 | 2.81E-04 |
| F16 | |||||||
| M | –1.0316 | –1.0316 | –1.0316 | –1.0316 | –1.0316 | –1.0316 | –1.0316 |
| B | –1.0316 | –1.0316 | –1.0316 | –1.0316 | –1.0316 | –1.0316 | –1.0316 |
| W | –1.0316 | –1.0316 | –1.0316 | –1.0316 | –1.0316 | –1.0316 | –1.0316 |
| SD | 4.15E-06 | 1.28E-14 | 2.28E-16 | 2.73E-10 | 2.80E-06 | 2.28E-16 | 1.28E-16 |
| F17 | |||||||
| M | 0.3980 | 0.3978 | 0.3978 | 0.3978 | 0.3978 | 0.3978 | 0.3978 |
| B | 0.3978 | 0.3978 | 0.3978 | 0.3978 | 0.3978 | 0.3978 | 0.3978 |
| W | 0.3989 | 0.3978 | 0.3978 | 0.3978 | 0.3978 | 0.3978 | 0.3978 |
| SD | 9.82E-05 | 9.33E-10 | 0 | 1.34E-08 | 2.53E-05 | 1.54E-07 | 1.73E-10 |
| F18 | |||||||
| M | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| B | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| W | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| SD | 2.50E-07 | 2.14E-09 | 5.09E-16 | 7.32E-08 | 3.29E-07 | 6.60E-16 | 1.39E-06 |
| F19 | |||||||
| M | –3.8556 | –3.8627 | –3.8627 | –3.8623 | –3.8619 | –3.8627 | –3.8627 |
| B | –3.8626 | –3.8627 | –3.8627 | –3.8627 | –3.8627 | –3.8627 | –3.8627 |
| W | –3.8546 | –3.8627 | –3.8627 | –3.8549 | –3.8559 | –3.8627 | –3.8626 |
| SD | 0.00236 | 1.76E-03 | 2.28E-15 | 4.13E-07 | 0.0023 | 2.24E-15 | 5.58E-05 |
| F20 | |||||||
| M | –3.0476 | –3.2585 | –3.2744 | –3.2585 | –3.2604 | –3.2506 | –3.2979 |
| B | –3.1881 | –3.3219 | –3.3219 | –3.3219 | –3.3219 | –3.3219 | –3.3219 |
| W | –2.6277 | –3.0838 | –3.2031 | –3.1390 | –3.0866 | –3.2031 | –3.2006 |
| SD | 0.1274 | 0.0629 | 6.0E-02 | 0.0662 | 0.0598 | 0.05975 | 5.80E-02 |
| F21 | |||||||
| M | –5.2182 | –10.1531 | –8.8855 | –9.6479 | –9.3927 | –6.00519 | –9.8983 |
| B | –10.0163 | –10.1531 | –10.1531 | –10.1531 | –10.1532 | –10.1531 | –10.1532 |
| W | –0.8805 | –10.1531 | –5.0551 | –5.1007 | –5.05519 | –2.6304 | –5.05519 |
| SD | 2.5812 | 2.58E-07 | 2.0781 | 1.8509 | 1.5551 | 3.2810 | 1.63E-07 |
| F22 | |||||||
| M | –5.5013 | –10.4029 | –10.1392 | –10.4029 | –10.1389 | –6.7722 | –10.4029 |
| B | –8.9717 | –10.4029 | –10.4029 | –10.4029 | –10.4029 | –10.402 | –10.4029 |
| W | –0.9097 | –10.4029 | –5.1288 | –10.4028 | –5.12861 | –1.83759 | –10.4029 |
| SD | 1.75E-06 | 1.75E-06 | 1.623339 | 1.1885 | 2.5810 | 3.7993 | 1.58E-06 |
| F23 | |||||||
| M | –6.2499 | –10.5364 | –10.5360 | –10.5363 | –10.5361 | –5.9184 | –9.9956 |
| B | –9.4500 | –10.5364 | –10.5364 | –10.5364 | –10.5363 | –10.5364 | –10.5364 |
| W | –4.9950 | –10.5364 | –10.5298 | –10.5363 | –10.5356 | –1.8594 | –5.1284 |
| SD | 1.6314 | 3.76E-06 | 1.1987 | 1.22E-05 | 2.200 | 3.6210 | 4.28E-07 |
表 II. 23个基准函数在20次独立运行中的最小化结果,针对F1‐F23
| 函数 | GWO | PSO | SCA | WOA | mGWO | PSO GSA | WOA‐mGWO |
|---|---|---|---|---|---|---|---|
| F1 | 8.01E‐09 | 8.01E‐09 | 8.01E‐09 | NA | 8.01E‐09 | 8.01E‐09 | NA |
| F2 | 8.01E‐09 | 8.01E‐09 | 8.01E‐09 | 7.90E‐09 | 7.42E‐09 | 8.01E‐09 | NA |
| F3 | 4.70E‐03 | 6.80E‐08 | 6.80E‐08 | 6.80E‐08 | 6.80E‐08 | 6.80E‐08 | NA |
| F4 | 6.80E‐08 | 6.80E‐08 | 6.80E‐08 | 6.80E‐08 | 6.80E‐08 | 6.80E‐08 | NA |
| F5 | 9.13E‐07 | 2.85E‐01 | 6.80E‐08 | 2.39E‐01 | 0.3369 | 9.75E‐06 | NA |
| F6 | 6.60E‐08 | NA | 6.60E‐08 | 6.60E‐08 | 6.70E‐08 | 6.56E‐08 | 6.60E‐08 |
| F7 | 3.24E‐01 | 6.80E‐08 | 6.80E‐08 | 5.65E‐02 | 6.80E‐08 | 6.80E‐08 | NA |
| F8 | 6.80E‐08 | 6.80E‐08 | 6.80E‐08 | 2.00E‐03 | 6.80E‐08 | 6.80E‐08 | NA |
| F9 | NA | 7.99E‐09 | 9.60E‐03 | NA | 8.01E‐09 | 8.01E‐09 | NA |
| F10 | 4.28E‐09 | 2.37E‐08 | 4.21E‐08 | 8.90E‐01 | 3.96E‐08 | 2.86E‐08 | NA |
| F11 | NA | 3.27E‐06 | 4.50E‐03 | NA | 3.30E‐06 | 4.14E‐04 | NA |
| F12 | 6.52E‐08 | NA | 6.52E‐08 | 6.52E‐08 | 6.65E‐08 | 6.57E‐08 | 6.52E‐08 |
| F13 | 6.64E‐08 | NA | 6.64E‐08 | 6.64E‐08 | 5.90E‐08 | 1.18E‐06 | 6.64E‐08 |
| F14 | 2.69E‐04 | 8.40E‐05 | 1.38E‐07 | 6.45E‐01 | 7.83E‐09 | 5.52E‐04 | NA |
| F15 | 1.60E‐05 | 7.70E‐03 | 4.68E‐05 | 4.39E‐02 | 0.1198 | 0.0273 | NA |
| F16 | 6.64E‐08 | 7.77E‐09 | 6.64E‐08 | 2.03E‐01 | 7.77E‐09 | 7.42E‐09 | NA |
| F17 | 1.43E‐07 | 7.99E‐09 | 6.79E‐08 | 7.64E‐02 | 1.05E‐07 | 2.50E‐06 | NA |
| F18 | 1.51E‐08 | NA | 1.51E‐08 | 1.51E‐08 | 1.42E‐04 | 4.02E‐01 | 3.33E‐09 |
| F19 | 8.01E‐09 | NA | 8.01E‐09 | 8.01E‐09 | NA | NA | 8.01E‐09 |
| F20 | 1.40E‐01 | 1.20E‐01 | 6.80E‐08 | 0.0239 | 0.4312 | 3.17E‐02 | NA |
| F21 | 6.80E‐08 | 2.78E‐01 | 6.80E‐08 | NA | 0.1014 | 0.031 | 2.29E‐01 |
| F22 | 6.80E‐08 | 1.06E‐04 | 6.80E‐08 | 0.0016 | 6.80E‐05 | 0.1707 | NA |
| F23 | 6.80E‐08 | 1.06E‐04 | 6.80E‐08 | 0.0016 | 2.86E‐08 | 1.47E‐01 | NA |
表 III. p值计算 用于威尔科克森秩和检验
测试(内纳瓦特和库马尔·贾托思,2017)在5%显著性水平下,通过比较每次运行的p值来确定其优越性,如表III所示。由于最佳算法无法与自身进行比较,因此对每个函数均用不适用(NA)表示。然而,混合WOA‐mGWO在大多数基准函数上得到的p值远小于0.05,表明该算法具有统计显著性,仅函数F21除外。因此,混合WOA‐mGWO算法的整体性能证明了其在文献中优于其他竞争算法。
4. 成本函数的构建
电路-论述了使用混合WOA‐mGWO算法对模拟电路中的MOS晶体管几何比例进行层级实现与优化。在此,初始化约束条件和工艺参数以获得设计参数,即晶体管的宽长比、偏置电流(Ibias)和电容值。该过程首先由设计者指定范围内随机初始化参数,随后聚焦于成本函数的优化。当满足终止条件时,该算法将得到使成本函数最优的设计参数新值。
所选用于优化的电路案例是一个两级传统的CMOS运算放大器,采用如图8所示的密勒补偿拓扑结构。混合WOA‐mGWO算法的目标是在满足运算放大器的直流增益(Av)、单位增益带宽(UGB)、压摆率(SR)、共模电压(VICmin和VICmax)、功耗(Pd)以及负载电容(CL)等目标规格的前提下,减小整体MOS晶体管面积。
为了减轻沟道长度调制的影响,MOS晶体管的沟道长度取值大于最小晶体管长度,即Li= 1 μm对于 i= 1到 8。运算放大器的设计参数包括晶体管的宽度(Wi对于 i= 1到 8)、电容’值(CC和 CL)以及 Ibias。在施加适当的匹配特性后,晶体管M1、M3和M5分别与M2、M4和M8相同。用于设计运算放大器的经验公式在附录中进行了说明(Allen and Holberg, 2002)。
混合WOA‐mGWO算法的初始种群大小被视为一个大小为(粒子数量(P) ×粒子向量(Q)) 的矩阵,其中P = 60且Q = 7。用于两级CMOS运算放大器优化设计的粒子向量如下:
$$X_{opamp} = [Av, CL, SR, VICmin, VICmax, UGB, Pd]$$
(13)
这里,成本函数被定义为所有晶体管所占用的总MOS面积(宽度 ×长度的总和),其表达式如下:
$$CF = \sum_{i=1}^{N} (W_i \times L_i)$$
(14)
其中,N 是电路中的晶体管总数,且要求给定电路的成本函数期望值小于 300 μm²。因此,采用混合WOA‐mGWO算法来获取成本函数的最优值。
5. 结果与讨论
两个的优化设计-两级运算放大器,如图8所示,其目标是在满足Av、电容CL、压摆率SR、VICmin、VICmax、单位增益带宽UGB 和Pd等约束条件下(见表IV第2列),减小整体的MOS晶体管面积。用于优化该约束面积优化问题的约束处理技术为静态惩罚函数,这是电路尺寸设计工具中最常用的约束处理技术之一(Liu et al., 2009)。通过MATLAB采用混合WOA‐mGWO算法获得的MOS晶体管宽长比,被用于在Intel Core i7 4790 CPU@3.60 GHz、16GB内存的平台上,基于Cadence IC616进行运算放大器的电路级实现。
表V 展示了使用混合WOA‐mGWO及其他相关算法获得的两级运算放大器的最优设计参数。fi器优化设计的优化趋势以收敛图的形式示于fi中,如图9所示。该收敛图显示了不同的可行解
| 设计规格 | 目标 | PSO | WOA ALC‐PSO | GSA | AGSA | SCA | WOA‐mGWO |
|---|---|---|---|---|---|---|---|
| Av(dB) | >60 | 59.19 | 74.08 | 90.85 | 60.14 | 81.13 | 80.05 |
| 增益带宽积 (MHz) | >3 | 3 | 3 | 112.5 | 3.136 | 3.29 | 4.28 |
| 相位裕度 (度) | >45 | 63.53 | – | 66.5 | 47.53 | 57.91 | 62.00 |
| 压摆率 (V/μs) | >10 | 18.35 | 10 | 161.4 | 10.29 | 12.34 | 12.19 |
| 功耗 (mW) | <2.5 | 0.184 | 1.137 | 0.018 | 1.053 | 0.332 | 0.164 |
| 负载电容 (pF) | >7 | – | 7 | 0.05 | 10.02 | 10 | 8.1 |
| VICmin(V) | >0.3 | – | –0.01 | –0.85 | –0.86 | –1.22 | – |
| VICmax(V) | <1.6 | – | 1.1 | 0.95 | 1.8 | 1.79 | – |
| 共模抑制比 (dB) | >60 | 67.08 | – | 88.94 | 81.99 | 84.6 | 81.10 |
| 电源抑制比þ(dB) | >70 | 63.84 | – | 88.94 | 77.36 | 97.45 | 104.17 |
| PSRR‐ (分贝) | >70 | 99.16 | – | 100.3 | 86.82 | 84.86 | – |
| 面积 (mm²) | 目标 | 28.52 | 93.86 | 10.91 | 114.6 | 70.32 | 28.02 |
| FOM 运算放大器 最大 | – | – | 0.43 | 5.625 | 0.69 | 1.09 | 2.67 |
| 技术 (mm) | 0.18 | 0.18 | 0.13 | 0.35 | 0.35 | 0.18 | 0.18 |
| 运行时间 (秒)最小 | – | – | – | 198.4 | 308 | 0.418 | 0.454 |
表 IV. 获得的结果 使用混合WOA‐ mGWO及其 比较,使用 不同算法
| 设计参数 | 基于仿真的 | 基于方程的 |
|---|---|---|
| GSA | AGSA | |
| W1/L1(毫米/毫米) | 4/2 | 4/2 |
| W3/L3 (mm/mm) | 4/2 | 4/2 |
| W5/L5 (mm/mm) | 4/2 | 4/2 |
| W6/L6 (毫米/毫米) | 21.94/2 | 7.16/2 |
| W7/L7 (毫米/毫米) | 11.36/2 | 4/2 |
| W8/L8(毫米/毫米) | 4/2 | 4/2 |
| I bias(mA) | 45.28 | 30 |
| 电容 (pF) | 4.4 | 2.2 |
 混合WOA-mGWO算法在电路优化中的应用
混合WOA-mGWO算法在电路优化中的应用




















 607
607

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








