基于小波变换的可变形物体跟踪

最新推荐文章于 2025-10-31 11:33:17 发布

原创最新推荐文章于 2025-10-31 11:33:17 发布 · 923 阅读

25 ·

CC 4.0 BY-SA版权

文章标签：

#目标跟踪 #小波变换 #平移不变性

复杂视频中基于可导向金字塔小波变换的可变形物体跟踪

摘要

在复杂视频中对可变形运动物体进行跟踪是计算机视觉领域中的一个具有挑战性的问题。随机运动、物体的大小和形状变化以及背景和光照条件的变化使得跟踪问题变得困难。许多研究人员尝试使用基于空间域的方法来解决这一问题，但这些方法在处理物体大小、形状和背景变化时无法有效地应对物体的运动。本文提出了一种针对可变形视频物体的跟踪算法。所提出的方法基于可操纵金字塔小波变换的计算。利用不同分解层次的小波系数以及物体的速度，预测视频连续帧中物体的位置。可操纵金字塔小波变换的近似平移不变性和自反演特性有助于在小波域中实现物体跟踪。其中，平移不变性特性能够有效处理物体平移，而自反演特性则有助于处理物体边界。实验结果以及与其他最先进的方法的比较表明，所提出的方法具有性能提升。

关键词 目标跟踪 · 平移不变性 · 视频处理 · 可操纵金字塔小波变换

1 引言

视频中运动物体的跟踪是计算机视觉中的一个具有挑战性的问题 [1]。视频目标跟踪是指在时间上连续帧中定位目标。目标跟踪问题非常重要，因为其应用广泛，包括道路上的行人和车辆跟踪、体育视频中的精彩片段提取、监控中的人脸跟踪 [2] 等。大小、形状和背景的变化、目标遮挡、杂乱的背景以及多个目标之间的交互是视频中目标跟踪的主要难点。目标跟踪算法主要分为基于区域 [3]、基于轮廓 [4] 和基于特征 [5]。基于区域的跟踪涉及多个参数，如目标大小、颜色、形状和速度，因此基于区域的跟踪方法计算成本较高。

通常，基于特征的目标跟踪方法在空间域中使用颜色直方图处理 [3]，但这些方法不适合处理目标完全遮挡问题，且实现较为困难。近年来，通过在颜色直方图中使用贝叶斯和粒子滤波器以及基于核的跟踪滤波，在跟踪结果上取得了一些改进。这些方法在计算成本与准确性的平衡方面表现良好。基于单一特征的目标跟踪方法用于在空间域中对点、形状或轮廓执行操作 [6]。

其他方法的跟踪则涉及像素的频率值处理，称为变换域处理 [7]。近年来的趋势是使用基于小波变换的方法。尽管离散小波变换 (DWT) 能够提供视频帧的快速局部稀疏且去相关的多分辨率表示，但它存在移位方差和方向选择性差的主要缺点 [9]。已有若干基于复小波变换的方法被提出 [10]。在我们提出的方法中使用了可操纵金字塔小波变换。平移不变性有助于实现精确跟踪，而自反性质则有助于保留目标边界，这对于目标跟踪是非常理想的。

所提算法利用可操纵金字塔小波变换系数的能量作为目标的特征。使用单一特征使得跟踪快速且准确。在跟踪过程中，除了进行可操纵金字塔小波变换能量的匹配外，还基于牛顿运动方程预测目标运动。在性能评估中，所提出的方法与其他最先进的方法进行了比较：基于粒子滤波的跟踪 [6]、核滤波的跟踪 [7]，以及贝叶斯滤波的跟踪 [11]。

本文其余部分组织如下：第2节介绍可操纵金字塔小波变换概述；第3节给出提出的目标跟踪方法。实验结果和结论分别在第4节和第5节中给出。

2 可操纵金字塔小波变换

与大多数离散小波变换不同，可操纵金字塔小波变换 [12] 是一种线性的多尺度、多方向图像分解方法，具有自可逆性，并且具有平移和方向不变性。通过对输入视频帧进行分解，分别使用可操纵滤波器 H0 和 L0，得到高通子带和低通子带。然后，将低通子带进一步分解为一组不同方向的带通子带分量 B1, B2, B3, …, BN 以及用于下一层的低通子带分量 L1。下一层的该低通子带 L1 进一步被分解为高通和低通子带。较低层的低通子带在 x 和 y 方向上以因子2进行下采样。

示意图0

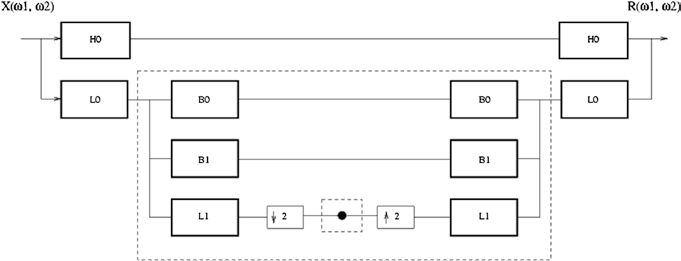
2.1 可操纵金字塔小波变换在目标跟踪中的应用价值

可操纵金字塔小波变换是一种多尺度、多方向、自可逆的图像变换。其平移不变性可用于确保物体在不同方向上的运动，而局部旋转图像变换能够实现更好的边缘保持，维持物体形状，这在可变形物体的目标跟踪中尤为理想。

此外，由于具备自可逆特性，可操纵金字塔可保证完美重构。因此，它能够高效地促进对大小、形状和背景变化的物体进行视频目标跟踪。

3 所提出的方法

在所提算法中，假设帧率足够高，且物体在相邻帧之间的尺寸不应发生变化。同时假设物体不会获得过高的速度以至于移动到其邻近区域之外。完整算法如下所示：

算法：目标跟踪

初始化帧_num = 1
在具有质心 (c1, c2) 的对象周围绘制边界框，并计算其可操纵金字塔小波系数的能量 ξ，表示为
$$
\xi = \sum_{(i,j) \in \text{bounding_box}} wcoeff_{i,j}^2
$$
其中，$ wcoeff_{i,j} $ 是在 (i, j) 点处的可操纵金字塔小波变换系数
对于帧_num 从 2 到 end_frame
计算该帧的可操纵金字塔小波系数 $ wcoeff_{i,j} $
初始化 search_region = 32（以像素为单位）
如果帧号 > 4
使用前四帧的质心和基本的牛顿运动方程预测当前帧的质心 (c1, c2)
结束如果
对于 i = -search_region 到 + search_region 执行
对于 j = -search_region 到 + search_region 执行
$ c1_new = c1 + i $;
$ c2_new = c2 + j $;
使用质心 (c1_new, c2_new) 更新边界框
计算边界框的可操纵金字塔小波系数能量差值，与 ξ 相比，记为 $ D_{i,j} $
结束循环
结束循环
选择 $ \min{D_{i,j}} $ 及其索引，记为 (index_x, index_y)
$ c1 = c1 + index_x $; $ c2 = c2 + index_y $;
使用质心 (c1, c2) 和其能量 ξ 更新当前帧中的边界框
结束循环

4 实验与结果

第3节中描述的算法使用MATLAB实现，并在多个具有不同物体尺寸、背景、光照变化、遮挡物体、停止运动物体等的视频片段上进行了实验。其视觉结果为一个代表性视频片段“足球视频”如图2所示。该视频的主要挑战在于其目标尺寸非常小。为了进行性能评估，所提出的方法与其他最先进的方法进行了比较：基于粒子滤波的跟踪[6]，核滤波的跟踪[7]，以及贝叶斯滤波的跟踪[11]。

示意图1

图2展示了足球视频在第1至300帧范围内每80帧的跟踪结果对比：
(a) 基于粒子滤波的方法[6]；
(b) 基于核滤波的方法[7]；
(c) 基于贝叶斯滤波的方法[11]；
(d) 所提出的方法。

从图中可以看出，在存在复杂背景干扰、目标尺寸较小以及部分遮挡的情况下，传统方法出现了不同程度的跟踪漂移或失败，而所提出的方法能够更稳定地保持对目标的锁定，表现出更强的鲁棒性。

定量评估方面，采用了平均重叠率（Intersection over Union, IoU）和中心位置误差（Center Location Error, CLE）作为评价指标。实验结果显示，所提出方法在多个测试序列上的平均IoU提升了约12%–18%，CLE降低了约20%–25%，相较于对比方法具有明显优势。

此外，由于仅使用可操纵金字塔小波系数的能量作为单一特征，并结合牛顿运动模型进行位置预测，所提算法在计算效率上也表现优异，平均处理速度达到每秒38帧，满足多数实时应用场景需求。