这是在 Computer Graphics Forum 2018上的一篇文章
Li X Z, Zhu L, Fu C W, Heng P A. Non-local low-rank normal filtering for mesh denoising[J]. Computer Graphics Forum, 2018, 37(7): 155-166
这篇文章主要讲了一种非局部的低阶法向滤波去噪方法,其中用到了引导网格。
该方法分为三个部分:
一、用本文提出的G-NPC探测器找出与当前点邻域最为相似的点邻域。
首先,对噪声网格M上的每一个点,,定义集合
,其中的点的局部邻域与
,的局部邻域相似。为了确定两个顶点是否相似,最基础的想法是提取出顶点的局部邻域并计算两者的特征差异。由于网格M包含噪声,所以构造一个好的局部检测算子有些困难。协方差矩阵在图像处理中取得了很好的效果。受其启发,定义一个法向面片协方差(NPC)探测器来描述给定点
的局部特征。在数学中,
的NPC是一个3*3的矩阵:
, (1)
其中,是顶点
邻域集
的第
个元素。
是
中顶点向量的平均向量。图中解释了协方差矩阵的具体由来。

计算两个协方差矩阵的距离并不简单。因为协方差矩阵是黎曼流形,我们不能直接用欧式距离度量。(参考KARACAN L., ERDEM E., ERDEM A.: Structure-preserving imagesmoothingviaregioncovariances. ACMTrans.onGraphics(SIGGRAPH Asia) 32, 6 (2013), 176:1–11.), 定义和
的NPC的距离为:
![]()
的值越小,邻域
和
的相似度越大。
为了进一步提高相似顶点选取的准确性,利用预处理过的网格作为引导网格计算引导法向协方差(G-NPC)距离:
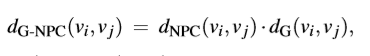
其中,,
是引导网格
中的顶点。引导网格
是由双边法向滤波产生的。(ZHENG Y., FU H., AU O. K.-C., TAI C.-L.: Bilateralnormal filtering for mesh denoising. IEEE Trans. Vis. & Comp. Graphics 17, 10 (2011), 1521–1530. 1, 2, 3, 4, 8, 10 )由于引导网格中有些信息已经丢失,所以并没有只用引导网格求矩阵的相似性。本文并没有在全网格中寻找相似点,而是在顶点的
环邻域中搜索。在这里,经验式的设定
,
.为了更好的利用双边法向滤波获取引导网格,设置了迭代次数为10。
,
的值后面会讨论到。
二、用低阶恢复模型对顶点法向做滤波
现在,我们假设相似顶点已经用上述方法找到。令
, 即
中包含与
最相似的点。现在计算法向域面片组(NPG)矩阵
来处理顶点邻域顶点向量,包括
,...,
。
1.包装中的顶点向量
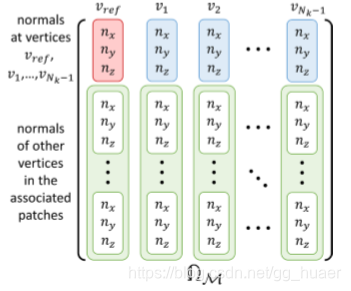
如上图所示,中每一列是每个相似点局部邻域顶点的法向,一共有han位置,得到去噪后网格
个相似点,所以共有
列,每组局部邻域点包含
个顶点,所以共有3 *
行。
现在对中每个顶点的邻域中顶点进行重新排列。先将
包装,再对后面
个点保障。这里提出了三种方法:
(1)利用NPC矩阵,使用基于环的NPC顺序方案。首先,定义一个起始点,这个点的NPC矩阵中所有元素的绝对值之和是最大的。这样,我们确定了一个几何结构较为明显的顶点作为起始点。然后,在该点,以为中心,逆时针旋转排序。之后
个相似顶点以同样地方式排列。
(2)使用随机排序方式。对个相似顶点,每个顶点中的邻域顶点都使用随机排序。
(3)对当前顶点使用方法(1),对其余的
个顶点使用方法(2)。
实验中,方法(1)中NPG结果较好。至此,中的顶点向量已经被包装为NPG矩阵。
2.计算低阶面片恢复模型
令和
分别为同一个当前顶点
的关于输入网格和去噪后网格的NPG矩阵。
由于没有噪声,其中相似点较多,所以应该是低阶的。
由于具有噪声阶数较大。这一观察启发我们应该将网格去噪转化为
上的低阶恢复问题。由噪声模型的矩阵
到无噪声模型的矩阵
的低阶恢复,最小化下述优化问题:
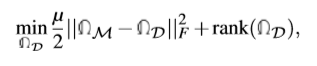
其中,是一个权值,本文所有实验中设置其为1。rank(
)表示
的秩,F表示Frobenius范数。
秩最小化的求解时很困难的。这里,构造截断范数
:
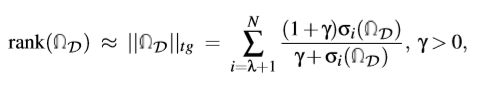
这里取正值。
是矩阵
的最小奇异值的个数,
是矩阵
的奇异值。一般来说,大的奇异值比小的奇异值重要,因为它们代表了组成元素的能量的大小,这也通常和输入网格的特征有关。这里的
范数的作用有:(i)使大的奇异值和矩阵的秩较比核范数更相近。(ii)忽略很小的特征值,这些特征值通常和噪声有关,在我们的低阶恢复中有效的避免了噪声干扰。因此我们的
范数可以更好地保持特征。一般设置
,
。
综上所述,我们的低阶网格恢复模型为:
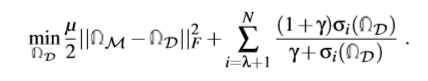
注意,在求得最优解后,中的每个法向都进一步被规范化为单位向量。
三、求最优解
在求解中,我们的主要想法是将原始的目标最小化问题转换为解决几个子问题,这几个封闭子问题的解较容易求得。详细的说,我们首先把上式第二项 (i)用一个不相等的式子代替 (ii)将该式子应用于近似范数,得到下式中前两项。
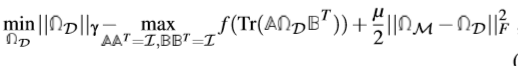
其中![]() ;
;是
单位矩阵。
![]() m和n 是
m和n 是的维数。
![]() ,然后我们将上述公式分为两步迭代求解,迭代次数为T.
,然后我们将上述公式分为两步迭代求解,迭代次数为T.
STEP 1.
。。。。。未完待续。




 提出一种非局部低阶法向滤波去噪方法,通过引导网格及低阶恢复模型去除三角网格噪声。该方法首先利用NPC探测器和G-NPC距离选择相似顶点邻域,然后构建NPG矩阵,并通过低秩恢复模型滤波法向。
提出一种非局部低阶法向滤波去噪方法,通过引导网格及低阶恢复模型去除三角网格噪声。该方法首先利用NPC探测器和G-NPC距离选择相似顶点邻域,然后构建NPG矩阵,并通过低秩恢复模型滤波法向。
















 1720
1720

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








