之前的两篇文章我们介绍了与DFS相关的回溯问题和洪水填充问题,其核心思想是“一条道走到黑”。是解决组合、回溯、存在性判断等问题的经典算法。但是当问题数据量变大、状态空间爆炸时,DFS 的劣势就显现出来:它可能会无意义地搜索深层路径,甚至因为指数级的分支增长而难以在合理时间内找到最优解。
比如说,我们想要求一个人在迷宫中从起点到终点所走的最小步数。DFS确实可以枚举所有路径,但是要么完整遍历图,要么需要复杂的剪枝流程。这么做的时间开销无疑是很高的,而且存在很高的浪费。我们不妨采用一种“按层扩展”的思路,当第一次抵达终点时,就能证明这条路径是最短的,这种策略就是BFS(广度优先搜索)。如果说DFS是在探寻有没有解,那BFS就是在有条不紊地探寻最优解。实际上DFS或者BFS两种方法的选择,我们需要思考,这道题目的搜索策略是需要“深入”,还是“扩散”?BFS题目的一大前提条件是任意两个节点相互之间的距离相同,绝大多数情况下是无向图下的场景。
BFS通过维护队列结构,层层推进,适合求解最短路径、层次传播、多源扩散等类型的问题,也能在状态空间搜索中以最小代价找到答案。今天我们将从最基础的层序遍历出发,一步步深入到多源 BFS、状态压缩 BFS、双向 BFS 等高阶应用,看看BFS的思维如何在图、网格乃至复杂状态空间中发挥不可替代的作用。
leetcode 102 二叉树的层序遍历
这道题相信对有一定做题量的朋友来讲相信一定是再熟悉不过了,我本人做这道题的次数也不下五遍了,而且在之前介绍二叉树遍历的时候也讲过这道题。但正是这道“烂大街”的题目,是我们了解BFS思想的最佳窗口了。如果这道题我们使用的是DFS思想的话,是一个“走到底再回来”的过程,假如遍历到左子树,那么会“暂时忘记右边的节点”,这样其实无法做到维护全局层次信息的。熟悉DFS的朋友们一定了解DFS的特性与其底层的LIFO栈结构密切相关。而如果需要实现层次遍历我们必须保证“顺序性”,所以我们需要维护一个FIFO队列结构。而我们可以通过队列是否为空来区分层数,这是一个天然的优势。具体的实现细节不再过多赘述,朋友们可以通过这道题重点养成一下写BFS的大概感觉,我们重点分析后面难度较高的题目,示例代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> res;
if(!root){
return res;
}
queue<TreeNode*> q;
q.push(root);
while(!q.empty()){
int n=q.size();
vector<int> currentLevel;
for(int i=0;i<n;i++){
TreeNode* node=q.front();
q.pop();
currentLevel.push_back(node->val);
if(node->left!=nullptr){
q.push(node->left);
}
if(node->right!=nullptr){
q.push(node->right);
}
}
res.push_back(currentLevel);
}
return res;
}
}; 
这道题可以说是一道相当经典的多源BFS例题了。上面是leetcode给出的示例,输出矩阵的每个位置代表从该位置到最近的 0 的距离。我其实一上来就会想从每个1出发,找与其最近的0,但是那样其实需要对每个1都进行一次BFS,存在超时风险!正难则反,我们不妨从每个0出发,然后一圈一圈向外扩展,当每个1第一次被访问的时候,就可以计算出到最近的0的距离。很精妙,这个距离正是由层数来维护的!这也就是BFS的强大之处之一--利用层数维护距离。每一次出队入队,代表距离+1。在网格图中,我们常常维护的是节点的横纵坐标,在C++中可以用pair对组维护。在扩展过程中,为了防止已访问的空间导致不必要的时间开销,我们可以维护一个标记矩阵dist,同时可以借此记录答案。示例代码如下:
class Solution {
public:
vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
int n=mat.size();
int m=mat[0].size();
vector<vector<int>> dist(n,vector<int>(m,-1));
queue<pair<int,int>> q;
//0作为BFS起点
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (mat[i][j] == 0) {
dist[i][j] = 0;
q.push({i, j});
}
}
}
vector<pair<int,int>> dirs={{-1,0},{1,0},{0,-1},{0,1}};
while(!q.empty()){
auto[x,y]=q.front();
q.pop();
for(auto[dx,dy]:dirs){
int nx=x+dx;
int ny=y+dy;
if (nx >= 0 && nx < n && ny >= 0 && ny < m && dist[nx][ny] == -1) {
dist[nx][ny] = dist[x][y] + 1;
q.push({nx, ny});
}
}
}
return dist;
}
};题目给了我们一个二维网格图,在这个网格图中,0代表未放橘子的空格,1代表新鲜的橘子,2代表腐烂的橘子,腐烂的橘子会以分钟为单位向上下左右四个方向腐化新鲜的橘子,需要我们求所有橘子全部腐烂的最小分钟数。在这道题目中,初始情况有可能存在多个腐烂的橘子,这些腐烂的橘子会同时腐化新鲜的橘子,所以这是一道多源BFS的题目,以腐烂橘子作为BFS起点,上下左右相邻的新鲜橘子便是需访问的下一层节点。实际上,腐化的时间是由“层数”来进行维护的,我们的目标实际上就是求这个“最大层数”。这道题目中控制BFS过程的关键在于判断所有橘子是否全部腐化,所以我们需要先统计一下新鲜橘子的数量,之后在BFS扩散“腐化”过程中不断去减小这个数量,当新鲜橘子的数量减为0时,BFS过程结束,如果最后新鲜的橘子无法减为0,说明不可能将所有橘子腐化,返回-1即可。示例代码如下:
class Solution {
public:
int orangesRotting(vector<vector<int>>& grid) {
int n = grid.size();
int m = grid[0].size();
queue<pair<int,int>> q;
vector<pair<int,int>> dirs = {{-1,0},{1,0},{0,-1},{0,1}};
int fresh = 0;
int res = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == 2) {
q.push({i, j});
} else if (grid[i][j] == 1) {
fresh++;
}
}
}
while (!q.empty()) {
int sz = q.size();
bool changed = false; // 这一层是否有新橘子被感染
for (int k = 0; k < sz; k++) {
auto [x, y] = q.front();
q.pop();
for (auto [dx, dy] : dirs) {
int nx = x + dx, ny = y + dy;
if (nx >= 0 && nx < n && ny >= 0 && ny < m && grid[nx][ny] == 1) {
grid[nx][ny] = 2;
fresh--;
q.push({nx, ny});
changed = true;
}
}
}
if (changed) res++;
}
return fresh == 0 ? res : -1;
}
};
leetcode 2290 到达角落需要移除障碍物的最小数目
在这道题目中,我们有一个网格,0位置代表可以直接通过,而1位置存在障碍物,必须移除之后方可通过。我们需要求的是从左上角到右下角移除障碍的最少数量。我们不妨将这个问题抽象一下,我们把移除障碍看作一种“代价”。那么这道题就变成了,在一个网格图中,每条边的边权为0或1,求从起点到终点的最小代价。这看上去就是个最短路问题啊!
也许会有朋友会想用传统BFS,通过层次扩散的方式进行统计来求这个最小代价,但是在这道题目中是行不通的。因为传统BFS成立的前提是每条边的权重(代价)必须相等。比如说我们开头所提到的迷宫问题,每移动一步的代价是1,BFS每扩展一次,步数+1,因此BFS的层数恰好就是最短路的长度。但是如果遇到这种边权不相同的情况传统BFS的解法就崩了。拿这道题来说,如果使用的是普通BFS的策略,可能会找到一条路径,使得总步数最低,但是这条路径绕开了所有障碍。也就是说,这种策略可能会找到“步数最短”的路径,而不是“代价最小”的路径。
我们由此引入了一种特殊的方法:0-1BFS来解决这种类型的问题。0-1BFS本质上是Dijkstra算法的一种特化。实际上我们需要设计一种数据结构,能够将边权分别为0和1的边区别对待。于是我们便想到了双端队列这种数据结构(C++ STL库提供了deque容器)。0-1BFS的过程如下:
(1)数组dist[i]表示从源点到i点的最短距离,初始设为无穷大。
(2)源点进入双端队列,dist[源点]=0。
(3)双端队列头部弹出X
a:如果X是目标点,返回dist[X]表示从源点到目标点的最短距离
b:考察从X出发的每一条边,假设某条边去Y点,边权为W:
①如果dist[Y]>dist[X]+W,则找到了更小的边,处理,否则忽略该边。
②处理时,更新dist[Y]=dist[X]+W
如果W==0,Y从头部进入双端队列
如果W==1,Y从尾部进入双端队列
然后循环重复步骤(3)
(4)双端队列为空时停止
我们接下来通过一个例子来演示一下0-1BFS的过程。
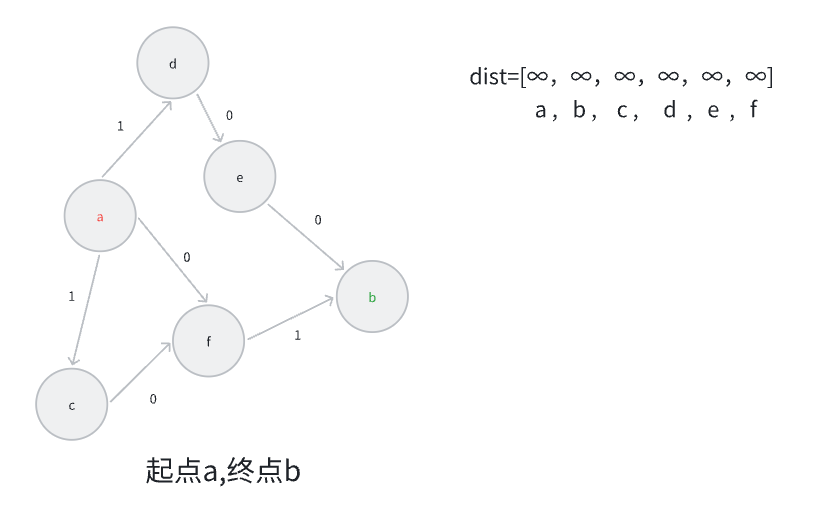
首先我们将源点a加入双端队列,并设置dist[a]=0。之后从队头弹出源点a,从源点a出发可以前往节点c,d,f,因为初始化的dist都是∞,拿节点c来说,dist[c]>dist[a]+1,所以更新dist[c]=1,同理dist[d]=1,dist[f]=0;与此同时,f从头部进入双端队列,c,d从尾部进入双端队列。之后我们从头部开始弹出节点f,从节点f出发可以前往节点b,由于dist[b]>dist[f]+1,所以更新dist[b]=1,同时b从尾部进入双端队列。接下来的过程与之同理,直到节点b第一次被弹出时,我们边求得了这个“最短路”,路径长就是dist[b]。不难发现,其实双端队列的精髓在于其内部设定了一个潜在的“优先级”,即优先处理边权为0的边,但是边权为1的边也不是直接不管,但是“得往后稍一稍”。那其实上面这道题目就完完全全是一道0-1BFS的模板题,基本上没什么出入,示例代码如下:
class Solution {
public:
int minimumObstacles(vector<vector<int>>& grid) {
vector<int> move = {-1, 0, 1, 0, -1};
int m = grid.size();
int n = grid[0].size();
vector<vector<int>> dist(m, vector<int>(n, INT_MAX));
deque<pair<int, int>> d;
d.push_back({0, 0});
dist[0][0] = 0;
while (!d.empty()) {
auto [x, y] = d.front(); // 获取 front 值
d.pop_front();//pop_front()是返回void的
if (x == m - 1 && y == n - 1) {
return dist[x][y];
}
for (int i = 0; i < 4; i++) {
int nx = x + move[i];
int ny = y + move[i + 1];
if (nx >= 0 && nx < m && ny >= 0 && ny < n && dist[x][y] + grid[nx][ny] < dist[nx][ny]) {
dist[nx][ny] = dist[x][y] + grid[nx][ny];
if (grid[nx][ny] == 0) {
d.push_front({nx, ny});
} else {
d.push_back({nx, ny});
}
}
}
}
return -1;
}
};本题可以算是互联网大厂面试笔试的高频难题了,难度着实不小,区分度也很高。这道题目给了我们一个词典,起始单词(不在字典)和目标单词(在字典中),接龙的规则是每个相邻的单词只能相差一个字母,且只能利用字典中已存在的单词进行接龙。如果我们把词典中每个单词视为图中的一个节点,相差一个字母的单词之间有一条边连接,这样便能实现隐式建图,我们在这个图上实现BFS统计层数便可以得到这个序列中的单词数目。但事实上这种方法是过不去的,当字典空间很大时,因为每个单词存在26*单词长度种变形,这个过程的时间复杂度是难以忍受的,我们必须去设计一种剪枝策略来降低解决该问题的时间开销。
我们设想一个问题,比如说我在北京,我朋友在上海。我们二人想要在最短时间内见面,也就是说我们俩的公共目标是找到北京与上海之间的最短路径,但显然由一个人去寻找是不公平的,时间开销也会更大,所以我们俩同时从北京和上海出发,我从北京开始不断寻找前往上海的最短路,我朋友从上海开始不断寻找前往北京的最短路。假如我们俩最终在某地相遇,那么将我们俩走过的路程进行拼接,就是北京与上海之间的最短路。那么在这道题中也一样,我以起始词作为源点开始BFS的时间开销既然太大,那不如同时从起始词和目标词出发,向中间搜索,这种思路就叫做双向BFS,十分之经典。我们可以通过smallLevel(从起始点开始,初始为{startword}),bigLevel(从目标点开始,初始为{endword})两个集合维护经过的节点。用一个nextLevel集合来维护从smallLevel出发扩展到的所有合法节点,其可能在下一轮变为smallLevel或bigLevel的一部分,每结束一轮都需要将nextLevel清空。词典dict中只维护剩余可用,尚未被访问的单词。双向广搜的核心策略是每轮总是扩展当前层中单词数量最小的一侧。在coding实现中,我们通常希望将这一侧统一到smallLevel上,所以我们需要涉及一个compare&swap的逻辑,这样我们就可以在主逻辑中一直以smallLevel集合为基准进行扩展了。
值得注意的是,这道题的图结构不是显式的。也就是说,图的边不是预先存好的,而是在BFS的过程中动态建立的。比如说"hit" → "hot" → "dot" → "dog" → "cog"这样的扩展过程中,从hot扩展到dot的过程中,会枚举每个位置变成“a-z”,然后判断这个单词是否在字典中。
class Solution {
public:
int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
unordered_set<string> dict(wordList.begin(), wordList.end());
if (dict.find(endWord) == dict.end()) {
return 0;
}
unordered_set<string> smallLevel;
unordered_set<string> bigLevel;
unordered_set<string> nextLevel;
smallLevel.insert(beginWord);
bigLevel.insert(endWord);
for (int len = 2; !smallLevel.empty(); len++) {
for (string w : smallLevel) {
string word = w; // 复制一份,用于修改
for (int j = 0; j < word.size(); j++) {
char old = word[j];
for (char change = 'a'; change <= 'z'; change++) {
if (change != old) {
word[j] = change;
if (bigLevel.find(word) != bigLevel.end()) {
return len;
}
if (dict.find(word) != dict.end()) {
dict.erase(word);
nextLevel.insert(word);
}
}
}
word[j] = old;
}
}
//compare&swap逻辑
if (nextLevel.size() <= bigLevel.size()) {
smallLevel = nextLevel;
} else {
swap(smallLevel, bigLevel);
bigLevel = nextLevel;
}
nextLevel.clear();
}
return 0;
}
}; 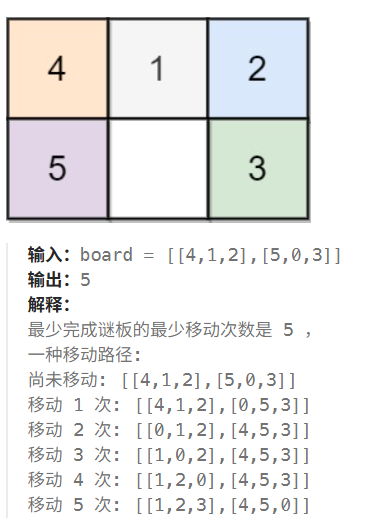
这道题颇有一点“智力题”的成分了。上图我贴出了leetcode官方给出的最复杂的一个示例,相信朋友们能够由此搞明白完成谜板的过程。当board为[[1,2,3],[4,5,0]]时谜板被解开。老实说刚开始思考这套题时还是感觉比较棘手的,因为每个小块的移动并非是独立的,它们之间存在强耦合关系,一个小块到目标位置的最短路径并不能保证全局最优,所以以每个小块为源点去跑BFS貌似是行不通的。
这种题目其实也非常考验我们的抽象思维了,既然不能从每个小块出发,那我们需要思考,还能通过什么指标来建立一些联系来帮助我们解题。我们不妨上升一个维度,设法把棋盘的状态作为搜索的单位,即视为一个节点。棋盘的状态是一个十分宽泛的概念,我们必须根据一种棋盘内部的特征对其进行组织,也就是说我们需要寻找连接节点之间边的定义。我们定义当且仅当两个状态之间只差一次合法交换时,它们所代表节点之间才存在边。这样我们便建立起了一张“状态图”,接下来在这张状态图上进行单源BFS即可,这种类型的题目也叫做“状态图BFS”。不难看出,状态图BFS问题的最大难点不在于BFS过程本身,而在于如何对问题抽象,合理建图。
然后回到这个题目,接下来的关键点就在于如何进行关系之间的判定,实际上因为谜板大小是固定的,且谜板面积并不大,我们完全可以制定一个规则将谜板中的元素序列化为字符串。可以在线性时间复杂度上实现对串中的元素的比较,这个时间开销是满意的。这样我们就把这个谜板给摊平了,比如说谜板 [ [1,2,3], [4,0,5] ] 就变成字符串 "123405"。这里我们需要注意这个字符串的下标和谜板中每个位置之间的对应关系,0可能会出现在谜板的任意位置,不同位置对应的移动策略不一样,和前面其他的BFS问题一样,我们需要规定出移动方向。之后的过程和我们前面所做的单源BFS没有区别,示例代码如下:
int slidingPuzzle(vector<vector<int>>& board) {
string start, target = "123450";
for (auto &row : board)
for (auto &x : row)
start += to_string(x);
vector<vector<int>> neighbors = {
{1,3}, {0,2,4}, {1,5}, {0,4}, {1,3,5}, {2,4}
};
queue<string> q;
unordered_set<string> visited;
q.push(start);
visited.insert(start);
int step = 0;
while (!q.empty()) {
int sz = q.size();
while (sz--) {
string cur = q.front(); q.pop();
if (cur == target) return step;
int zero = cur.find('0');
for (int nxt : neighbors[zero]) {
string newState = cur;
swap(newState[zero], newState[nxt]);
if (!visited.count(newState)) {
visited.insert(newState);
q.push(newState);
}
}
}
step++;
}
return -1;
} 通过今天的这些题目,我们发现BFS是一种按“层级”逐步扩张的搜索方式,核心思想是从起点出发,一层层向外扩展,直到找到目标状态。它常用于最短路径、状态转移、图遍历等问题。
BFS 的关键在于 队列(或双端队列)管理搜索顺序,以及 visited 去重 保证每个状态只访问一次。在复杂搜索中,还会引入 多源 BFS(多个起点同时出发)和 双向 BFS(从起点与终点同时扩张),以显著降低搜索空间。无论在网格、图论,还是状态压缩题中,BFS 的核心不变——从起点出发,分层扩散,最先到达目标的一定是最短路径。有不当之处还请多多指正与批评,我们一起成长!





















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








