之前我们对动态规划问题的演进过程,以及背包DP进行了介绍。今天我们就来介绍一种更加具有代表性,但是略有难度的题型:区间DP。这种题型同样也是一线互联网大厂历年笔试面试的常客,对于有志冲击互联网大厂的朋友是非常有必要吃透并掌握的。今天我选了几道非常经典的区间DP题目进行介绍。总体来讲,区间DP问题的核心思想就是将大范围的问题拆分成若干小范围的问题来求解。区间DP的讨论方式有两种:①基于两侧端点讨论②基于范围上划分点讨论。此处声明,我的文章是我学习左程云老师算法课程的笔记回顾,也借鉴了许多包括灵茶山艾府等其他大神的题解,在这些基础上融入了我的个人思考。
一.基于两侧端点的可能性展开
leetcode 1312 让字符串成为回文串的最小插入次数
上来就是Hard级别的王炸!不过朋友们别慌,题目难度是纸老虎,我们还是要拆解题意慢慢分析。题目对回文串的含义进行了阐述--正读和反读都相同的字符串。我们考虑这个问题还是要从回文串本身的性质出发。假设一个回文串s的左端点为l,右端点为r,则一定有s[l]==s[r],s[l+1]==s[r-1]...以此类推,直到回文中心点,有点双指针的感觉。基于上面这个性质,以及前面对于一些题目的介绍,我们需要假设一个最一般的场景。我们假设对于长度为n的字符串s而言,区间[l,r]上的子串已经回文,那么当i==0,j==n-1时,就说明整个字符串s回文!同理,我们假设dp[l][r]为使得区间[l,r]上的子串回文的最小插入次数,则dp[0][n-1]就是我们要求的解。
现在dp[l][r]的含义确定,我们就要开始状态转移方程的讨论。先看一些边界情况:如果l==r,单个字符直接就是回文串,返回0;如果l+1==r,即只有两个字符,如果二者相同为回文串,否则就必须插入一个与任意一个相同的字符凑成回文串,这个逻辑可以用三目来写。接下来我们基于区间的左右端点展开讨论:如果s[l]==s[r],那说明在[l,r]区间的最外侧已经形成了回文,此时我们只需要保证内侧回文即可,即讨论dp[l+1][r-1];如果s[l]!=s[r],那么有两种可能性,要么在[l,r]区间的左侧插入一个s[r],要么在[l,r]区间的右侧插入一个s[l]。有一个非常关键的点,DP不会追踪插入后的下标变化,区间DP中,dp[l][r]永远对应的是原始字符串的下标。实际上,我们不会真的插入字符,因为这样DP表无法固定,所以下面插入的过程都是假装的。这里可能会稍难理解,我举例说明:
s=[a,b,c,b,a,b,b,b,a] (l=2,r=6)
这是个非常一般的情况了,目前的讨论范围是[2,6],s[2]='c',s[6]='b',显然二者不相等。那么现在为了保证这个区间内的子串回文,我们有两种做法,①可以在s[2]位置处“插入”s[6]所代表的字符'b',此时s串就变成了:s'=[a,b,b,c,b,a,b,b,b,a],我们发现s[r]位置的b被匹配掉了,这里千万不要想成s[l]与s[r+1]配对。实际上,我们并没有真正的进行这个插入动作,而是单纯地认为s[r]被匹配了,此时问题就转化为使得[l,r-1]范围上的子串回文的最小插入次数,表示为dp[l][r-1]+1;②可以在s[6]位置处“插入”s[2]所代表的字符'c',此时s串就变成了:s''=[a,b,c,b,a,b,b,c,b,a],同理此时问题就转化为使得[l+1,r]范围上的子串回文的最小插入次数,表示为dp[l+1][r]+1。我们在两者之中取最小即可。示例代码如下:
class Solution {
public:
int minInsertions(string s) {
int n=s.size();
vector<vector<int>> dp(n,vector<int>(n,0));
for(int l=0;l<n-1;l++){
dp[l][l+1]=s[l]==s[l+1]?0:1;
}
for(int l=n-3;l>=0;l--){
for(int r=l+2;r<n;r++){
if(s[l]==s[r]){
dp[l][r]=dp[l+1][r-1];
}else{
dp[l][r]=min(dp[l+1][r],dp[l][r-1])+1;
}
}
}
return dp[0][n-1];
}
};二.基于范围上划分点的可能性展开
我们首先对题意进行分析。题目中说values[i]是第i个顶点的值(顺时针),我们需要注意,values数组中隐含了点的排列顺序。而且三角剖分一个多边形有一个隐含条件:剖分时内部不能存在交叉线。光看题目可能不是太好理解,我们举个六边形的例子,画个图来看看。
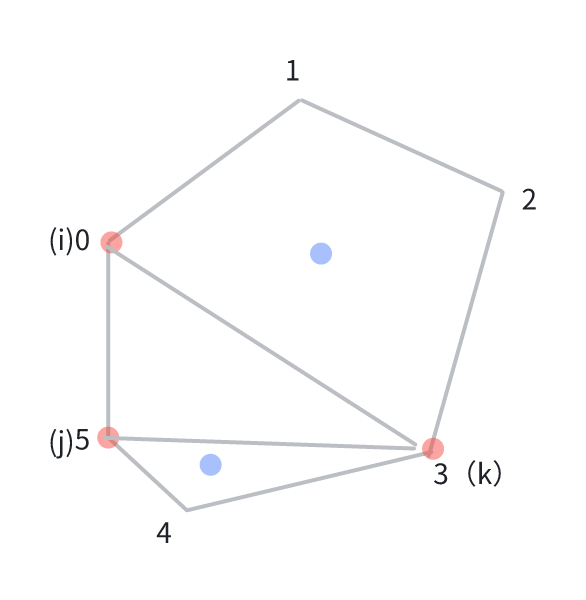
其实这道题追根溯源还是讨论多边形划分的可能性。不难发现,任何一条处于六边形外部的边,一定处于同一个三角形中,比如说边[0,5],我们将这条边“固定”。然后开始枚举除了标号0,5以外的点,比如说{0,1,5},{0,2,5}都可以构成三角形。实际上,在真正讨论的时候,每条边都应该被“固定”。我们假设values数组的长度为n(即n边形),定义dp[i][j]为从i顺时针出发到j的所有边加上边[j,i]组成n边形的最小分数,最后我们要求的就是dp[0][n-1]。当j-i<2的时候,根本不可能凑出封闭图形。我们假设底边为[i,j]的三角形顶点为k。那么这个多边形又被划分成了两部分(蓝色标出的部分)。我们的子问题就是在这个蓝色的部分,也就是i~k,k~j上继续进行剖分,计算总分就是三个部分的分数和。这个顶点k就是我们所说的“划分点”,也是这类题目的特征。经过上面的分析,我们的状态转移方程就很明确了,dp[i][j]=min(dp[i][j],dp[i][k]+values[i]*values[j]*values[k]+dp[k][j])。这道题的动态规划表比较有意思,我们来看一看:
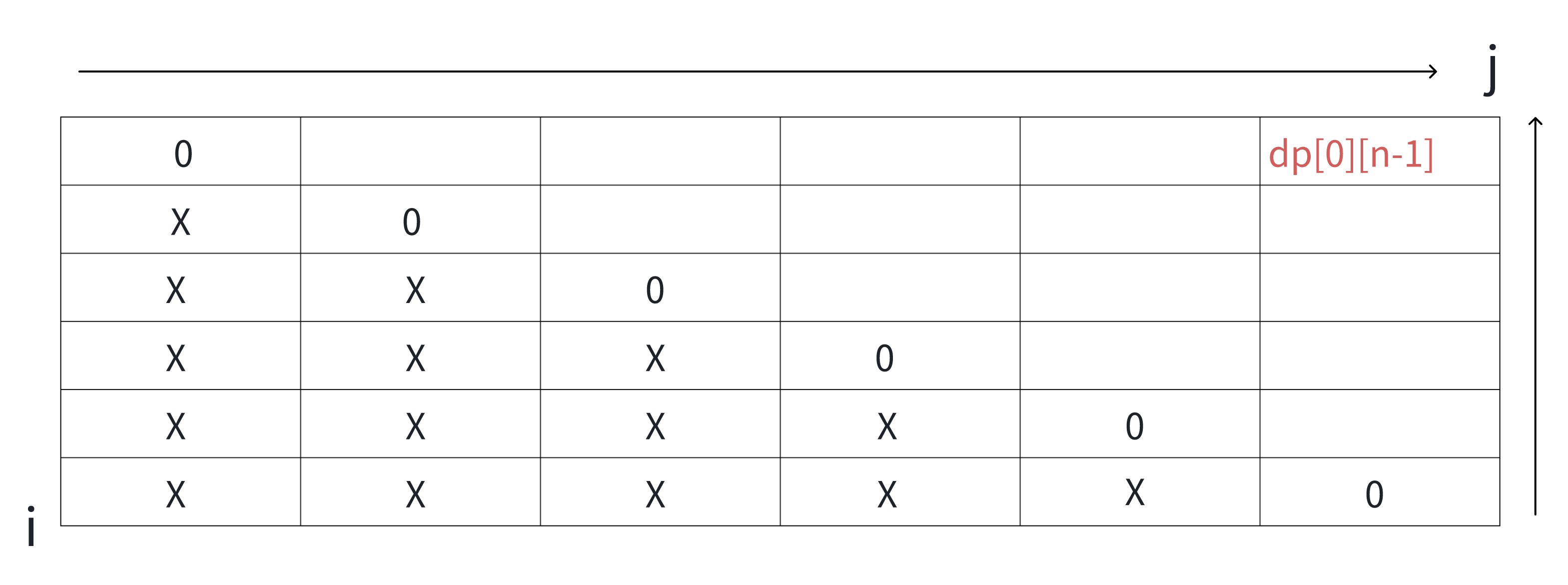
很显然,从我们的定义来看,i不可能超过j,所以dp表的左下半部分可以直接不填。当j-i=1时,根本不可能凑出封闭图形,那么分数就为0。填表的顺序是从左向右,从下到上。这道题的数据量有点大,我们需要做防溢出准备,用long long来接一把。示例代码如下:
class Solution {
public:
int minScoreTriangulation(vector<int>& values) {
int n = values.size();
vector<vector<int>> dp(n, vector<int>(n, 0));
// 从下往上、从左往右填表
for (int i = n - 3; i >= 0; i--) {
for (int j = i + 2; j < n; j++) {
dp[i][j] = INT_MAX; // 初始化 dp[i][j] 为最大值
for (int k = i + 1; k < j; k++) {
// 避免整数溢出:使用 long long 类型存储中间结果
long long temp = (long long)dp[i][k] + dp[k][j] + values[i] * values[k] * values[j];
// 将结果转换回 int 类型
dp[i][j] = min(dp[i][j], (int)temp);
}
}
}
return dp[0][n - 1];
}
};在理解题意之后我们不难发现,其实打印机的行为是“固定的”,就是打印由同一个字符所组成的序列。其实我拿到这道题目先想到的是利用贪心策略,这里我举个例子来回顾一下我的心路历程,也由此来和朋友们聊聊,什么题目适合用动态规划做,什么题目不适合。
假如字符串s="aaabaaa"。如果我们以局部最长覆盖的贪心策略,那么打印顺序应该是"aaa"->"aaab"->"aaabaaa",需要三步。但是这显然不是最优解,最优解是"aaaaaaa"->"aaabaaa",两步足矣,由此说明对于这道题而言局部最优未必等同于全局最优。对于贪心策略来讲,它只看眼前。但显然求这道题的最优解需要子区间的组合,也就是说这道题目是有后效性的,由此我们考虑用动态规划来做。
我们定义dp[i][j]为将[i,j]范围内的字符串打印为目标的最小次数。这里我们先来讨论一下边界情况,如果区间只包含一个字符,打印一次就完事。如果包含两个字符,看两个字符是否相同,写个三目判断下就行。这里有个挺巧妙的剪枝,如果[i,j]区间两端字符相同,我们可以不管[i,j]区间内都有什么字符,可以一股脑地从i出发覆盖到j-1位置,而不用管j位置,此时dp[i][j]=dp[i][j-1]。如果区间两端字符不同,那么内部一定存在划分点k了,在[i,k]区间上打印成i位置处的字符,在[k+1,j]上打印成j位置处的字符,此时dp[i][j]=dp[i][k]+dp[k+1][j],不断枚举取最小值即可。示例代码如下:
class Solution {public:
int strangePrinter(string s) {
int n=s.size();
vector<vector<int>> dp(n,vector<int>(n,0));
dp[n-1][n-1]=1;
for(int i=0;i<n-1;i++){
dp[i][i]=1;
dp[i][i+1]=s[i]==s[i+1]?1:2;
}
for(int i=n-3,ans;i>=0;i--){
for(int j=i+2;j<n;j++){
if(s[i]==s[j]){
dp[i][j]=dp[i][j-1];
}else{
ans=INT_MAX;
for(int k=i;k<j;k++){
ans=min(ans,dp[i][k]+dp[k+1][j]);
}
dp[i][j]=ans;
}
}
}
return dp[0][n-1];
}这道题可谓是相当经典了,是一线互联网大厂笔试面试的常客。我们如果把这些难题理解透了,那么对我们未来的求职的信心会有很大的促进作用。在理解题意之后,我们直接来参照着leetcode官方给的用例图来看看:
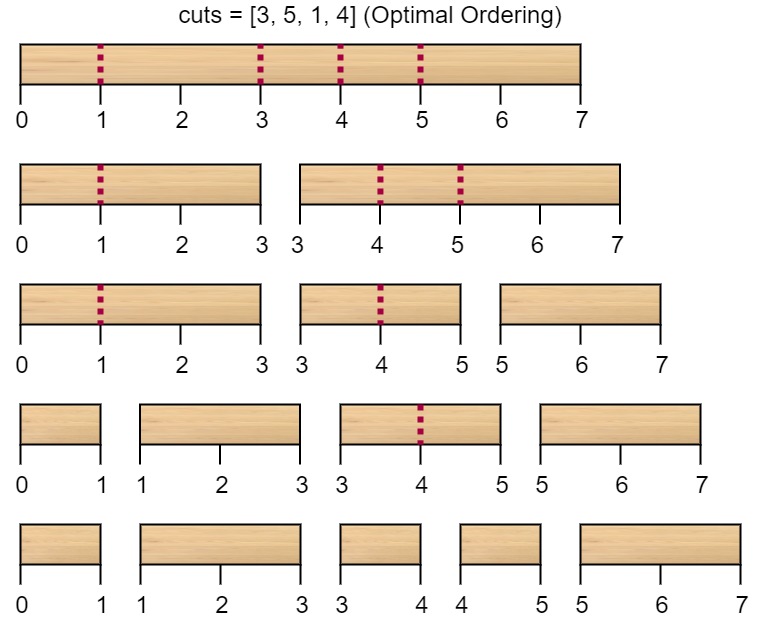
上面的图例给的很明确了,按照3,5,1,4的顺序依次对棍子进行切割,最终的成本为7+4+3+2=16。虽然切割点是固定的但是切割顺序是可以更改的。比如说采用1,3,4,5的切割顺序最终的成本就是20。所以这道题的关键其实就是枚举出一种最佳的切割方式。对于cuts数组来说,内部元素的顺序其实是可以人为调整的,那我们最好进行一轮排序预处理。而且实际上我们可以把这根棍子原始的左右端点视为“切割点”。所以上面图例的cuts数组就可以转化为[0,1,3,4,5,7]。这样做的好处就是我们可以很方便的通过作差算出任何分段的长度,即切这段棍子的成本。这是一种很常见的预处理方式,值得积累。
于是这个问题就转换成求切割左端点cuts[0]=0,右端点cuts[5]=7的棍子的最小成本。有些朋友可能会想:我贪心地切最长或者最短的棍子不就结了?错!因为未来切割次数和成本受子区间影响。我们再接着看切棍子的过程,假设第一刀就切在1处。那么左半边棍子的左端点cuts[0]=0,右端点cuts[1]=1;右半边棍子的左端点cuts[2]=1,右端点cuts[5]=7。后续的过程其实是相同的,由此拆解出了“子问题”,我们想到利用动态规划进行处理。
于是我们定义dp[i][j]为在左端点为i,右端点为j的棍子上进行切割的最小成本。那么dp[0][cuts.size()-1]即为所求。在[i+1,j-1]范围上枚举在切割点k(就是这道题目的“划分点”)切一刀的可能性:左半边棍子的左端点cuts[i],右端点cuts[k],切割的成本为dp[i][k];右半边棍子的左端点cuts[k],右端点cuts[j],切割的成本为dp[k][j],最后的成本和就是dp[i][k]+dp[k][j]+cuts[j]-cuts[i]。求出最小值就是我们需要的解,那么状态转移方程就很显而易见了。这里给大家一个小tips,我们填写动态规划表的方向往往是根据最终结果所在的位置定的。像这道题目所求为dp[0][cuts.size()-1],应当在dp表的右上角,所以填写方式是自下往上,自左往右,这决定了我们代码实现中写循环的方式。示例代码如下:
class Solution {
public:
int minCost(int n, vector<int>& cuts) {
cuts.push_back(0);
cuts.push_back(n);
ranges::sort(cuts);
int m=cuts.size();
vector<vector<int>> dp(m,vector<int>(m));
for(int i=m-3;i>=0;i--){
for(int j=i+2;j<m;j++){
int ans=INT_MAX;
for(int k=i+1;k<j;k++){
ans=min(ans,dp[i][k]+dp[k][j]);
}
dp[i][j]=ans+cuts[j]-cuts[i];
}
}
return dp[0][m-1];
}
};这道题和上面切棍子的题目有点类似,如果能充分理解切棍子的题意,那相信这道题也不难理解。每个气球标有数字存储在nums中,戳爆第i个气球会获得nums[i-1]*nums[i]*nums[i+1]的分数,我们想到了上道题目中的cuts数组。但这道题的关键是如果i-1或者i+1超过了数组的边界,则认为值为1。联想到上道题目预处理的过程,我们不妨也对nums数组进行预处理,首尾各插个1。因为实际上不存在这两个气球,所以我们不去遍历这两个位置,仅仅是求nums[i-1]或者nums[i+1]的值用。我们把处理过的数组记为arr,这样做能省去很多的边界讨论。
那可能有人说,这可太简单了,我贪心地打爆数值大的气球,错!因为在这道题中,因为邻居是谁比气球本身数值更关键。也许还会有朋友认为,这几乎和上面那道切棍子思路一模一样,切棍子问题是枚举先从哪开始切,那我们这道题就枚举先打爆哪个气球。别急,我们来一起分析一下。举个例子看:
arr=[1,a,b,c,d,e,1]
已知头尾两个“1”是我们预处理加进去的,不能当作气球被打爆,只是算值用的。假如我们先打c,那么左半部分还剩a,b;右半部分还剩c,d;b的右侧最近没爆的气球是d。再举个例子,比如先打d,那么左半部分还剩a,b,c;右半部分剩e。如果此时再打c的话,b的右侧最近没爆的气球是e。我们不难发现,打气球得分取决于被打气球的左右邻居。这时候问题来了,结算得分的时候,我们其实无法确定b左右两侧最近的没打爆的气球是什么。也就是说,如果我们从“先打爆谁”思路出发,随着打的顺序变化,邻居关系会动态改变,难以用固定区间来表示状态。类比前面切棍子问题,每次“切割”的代价取决于当前这段棍子的长度。无论你选择先切还是后切,切割区间的边界是固定的,所以可以用“枚举第一个切的位置”来做。所以这道题我们不能按气球谁最先被打爆进行尝试。但是换个角度来想想,最后一个被打爆的气球,其邻居一定是固定边界。我们根据这个范围每个气球谁最后被打爆来尝试,这样就能够很好的表达状态。这种思想就是所谓的“时间倒流”。
我们假设在区间(i,j)上(注意这里不包含边界i,j,为了和首尾插入1这个预处理语义统一)最后一个被打爆的气球是k,那么它的左右邻居就一定是i,j(由于其他气球都已经被打爆了)。定义dp[i][j]为区间(i,j)上所有气球都打爆得到的最大分数,则dp[i][j]=dp[i][k-1]+dp[k+1][j]+arr[i-1]*arr[k]*arr[j+1]。其实还是和前面切棍子实现方面有相似之处的,核心在于思考问题的方向不同。示例代码如下:
class Solution {
public:
int maxCoins(vector<int>& nums) {
int n=nums.size();
vector<int> arr(n+2);
arr[0]=1;
arr[n+1]=1;
for(int i=0;i<n;i++){
arr[i+1]=nums[i];
}
vector<vector<int>> dp(n+2,vector<int>(n+2,0));
for(int i=1;i<=n;i++){
dp[i][i]=arr[i-1]*arr[i]*arr[i+1];
}
for(int i=n,ans;i>=1;i--){
for(int j=i+1;j<=n;j++){
ans=max(arr[i-1]*arr[i]*arr[j+1]+dp[i+1][j],arr[i-1]*arr[j]*arr[j+1]+dp[i][j-1]);
for(int k=i+1;k<j;k++){
ans=max(ans,arr[i-1]*arr[k]*arr[j+1]+dp[i][k-1]+dp[k+1][j]);
}
dp[i][j]=ans;
}
}
return dp[1][n];
}
};这道题目也挺有趣的,同时也具有很高难度。题意不难理解,让我们合并连续的K堆石头,将其变为一堆,代价为这堆石头的总和。我们来思考一些特殊情况,题目中提到如果不能合并就返回-1,我们来看看无法合并的leetcode用例:
stones = [3,2,4,1], k = 3
每次操作都要合并三堆石头,而实际上我们会发现合并一次之后只剩下两堆石头,最后一步不可能完成。不难发现,从最终结果来看,把n堆石头合并为一堆,会减少n-1堆;而每次合并石头都会减少k-1堆,所以k-1必须是n-1的倍数,即取模为0,这是一个剪枝过滤条件。我们发现,每次合并所需的成本其实是依赖于上一步合并的结果的,也就是说这是个有后效性问题,存在依赖拓扑,由此我们考虑利用动态规划的方法来解。我们假设dp[i][j]为区间[i,j]上将所有石头合成一堆的最小成本,但这时候我们会发现一个问题:并不是所有子区间都可以直接合并为一堆。前面我们介绍过,假设区间长度为n,必须满足(n-1)%(k-1)==0才能严格收敛为一堆。假如n=5,k=3。从结果来看,全局确实可以合成为一堆,但是不是每个子区间都能合成一堆。比如某个子区间长度=2,就不能发生合并,但是这个区间可能可以合成 2 堆(保持原样),然后再跟外面的堆合并。也就是说用二维变参是无法完整表述上述状态的,我们需要进行升维。
我们定义dp[i][j][m]为在区间[i,j]上,将石头合并为m堆的最低成本。这样就可以表示所有的中间状态了。比如dp[i][j][2]的含义就是把 [i, j] 合并成 2 堆的最小代价(不要求直接合并成 1 堆),dp[0][n-1][1]即为所求。其实我们前面讨论的,在某个区间上能否直接将所有石头合并为一堆的问题正好就是这道题的可能性尝试。假如能够直接合并为一堆,那么dp[i][j][1]=dp[i][j][k]+sum(i,j)。如果不能,我们只能考虑分段合并,我们在[i,j]区间上枚举中间点t,于是dp[i][j][m]=dp[i][t][1]+dp[t+1][j][m-1](先把 [i, t] 合并成 1 堆,再把 [t+1, j] 合并成 m-1 堆)。由于这道题目可能涉及到求累加和的操作,我们可以考虑用前缀和预处理进行优化,防止在循环中一直求和导致超时。
我们这里再介绍一种更加严谨且不容易出错的循环写法:枚举区间长度。在这道题目中,写普通的三重循环实际上也没问题,但是在这道题中,我们必须保证在算 dp[i][j][m] 的时候,所依赖的 dp[i][t][1] 和 dp[t+1][j][m-1] 已经算好,这个情况是比较复杂的,有时候循环条件写不好往往会出一些意想不到的错误,然而枚举区间长度是一种相对稳妥的方法,朋友们可以参考下示例代码来看看是怎么写的。示例代码如下:
class Solution {
public:
int mergeStones(vector<int>& stones, int K) {
int n = stones.size();
if ((n - 1) % (K - 1) != 0) return -1;
// 前缀和预处理
vector<int> prefix(n + 1, 0);
for (int i = 0; i < n; i++) {
prefix[i + 1] = prefix[i] + stones[i];
}
const int INF = 1e9;
vector<vector<vector<int>>> dp(n, vector<vector<int>>(n, vector<int>(K + 1, INF)));
for (int i = 0; i < n; i++) {
dp[i][i][1] = 0;
}
for (int len = 2; len <= n; len++) {
for (int i = 0; i + len - 1 < n; i++) {
int j = i + len - 1;
for (int m = 2; m <= K; m++) {
for (int t = i; t < j; t++) {
if (dp[i][t][1] < INF && dp[t + 1][j][m - 1] < INF) {
dp[i][j][m] = min(dp[i][j][m], dp[i][t][1] + dp[t + 1][j][m - 1]);
}
}
}
if (dp[i][j][K] < INF) {
dp[i][j][1] = dp[i][j][K] + (prefix[j + 1] - prefix[i]);
}
}
}
return dp[0][n - 1][1];
}
};
这道题目我认为有很高的难度,属于实实在在的变态Hard水准。但相信通过之前的几道题目朋友们对区间DP已经形成了一定的题感,那不妨我们来挑战一下。题意不难理解,个人感觉有一点像前面“奇怪的打印机”这道题,但是思路是完全不同的。按照我们之前的思路,可能会定义dp[i][j]为在区间[i,j]上移除所有盒子的最大得分。但是其实定义之后我们发现状态转移方程是没法写的,因为我们遗漏了一个关键信息:在[i,j]区间外或者区间的某一侧,可能会存在和区间内某个盒子相同的盒子。而这些盒子在移除区间内其他盒子后可能会和区间内的同种盒子合并从而改变得分。然而移除盒子的得分公式严格依赖相同种类的盒子数量。这么说朋友们可能不好理解,我们还是举个例子来看看:
boxes=[1,2,1,2,1] i=0,j=2
根据我们上面的假设,子区间就是[1,2,1]。我们先独立看这个子区间,最优解是先移除2,再溢出两边的1,得分是1+2*2=5,根据我们之前的定义,dp[0][2]=5。但是在整个数组里,boxes[4]=1。当i=0,j=5时,我们的最优解是分别移掉两个2,然后同时移掉三个1,得分为1+1+3*3=11。不难发现,dp[0][2]是dp[0][5]的子问题,但是实际上dp[0][2]在整个方案中,并不是像我们之前,孤立地按照5来算的!因为boxes[4]处的1后来会与boxes[2]处的1发生合并。我们依旧看[0,2]这个区间,如果假定这个区间外某一点boxes[m]有一个1(同上例),且一定会和boxes[2]处的1合并,那么得分就不应该是5,而至少是1(移除2)+3*3(因为和区间外的1发生了一次合并)=10。这便产生了矛盾。和前面的打印机,切棍子,戳气球问题不同,它们子区间的最优解不会因为外部而改变。更直白的说,对于这道题目而言,区间 [i,j] 的最优解取决于外面是否有同种盒子。这种dp[i][j]的设定不成立的理由是状态缺少必需的上下文信息。
既然是缺少上下文信息,那我们有必要考虑对这道题目进行升维。这一点有点像上一道合并石头的题目。由此我们引入第三维参数k。既然我们前面讨论到,我们无法确定区间外的上下文状态,我们干脆以boxes[j]作为基准,定义k为区间[i,j]外和boxes[j]种类相同且已经连成一组的盒子数量。由于我们下一步要进行合并boxes[j],所以我们要求外部和boxes[j]同种的盒子是合并好的。于是,我们定义dp[i][j][k]为在boxes[i...j]中,假设j右侧已经有k个boxes[j]种类相同并与j连成一组的盒子(这些盒子是从j的右边被“带进来”的),那么把区间[i,j]处理完(连带这k个盒子)所能获得的最大分数。
我们开始讨论状态转移:有两种方案,首先可以直接把boxes[j]连同右边k个盒子一同移掉,获得(k+1)^2的分数。那剩下的子问题就是dp[i][j-1][0](k=0的原因是把j处理掉了,所以附带的盒子数归0)。还可以考虑把boxes[j]留着,先在区间内开刀。假设区间内有个位置m,满足boxes[m]=boxes[j],我们可以把这个m位置的盒子移动到最右边与j位置的盒子合并,之后再一并消掉。为了使m位置的盒子与j位置的盒子相邻,我们必须先把[m+1...j-1]上所有的盒子都消掉。于是这个问题转移为dp[i][m][k+1]+dp[m+1][j-1][0](我们先把[m+1...j-1]上所有的盒子都消掉得到dp[m+1][j-1][0],再把m,j连同外面k个盒子一同消了得到dp[i][m][k+1])。我们取这个过程的最大值即可,dp[0][n-1][0]即为所求。示例代码如下:
class Solution {
public:
int removeBoxes(vector<int>& boxes) {
int n = boxes.size();
vector<vector<vector<int>>> dp(n, vector<vector<int>>(n, vector<int>(n, 0)));
// 枚举区间长度
for (int len = 1; len <= n; len++) {
for (int i = 0; i + len - 1 < n; i++) {
int j = i + len - 1;
for (int k = 0; k <= i; k++) {
//直接移除 boxes[i] 以及前面k个相同的盒子
dp[i][j][k] = (k + 1) * (k + 1) + (i + 1 <= j ? dp[i + 1][j][0] : 0);
//尝试在 [i+1, j] 中找相同颜色,合并再移除
for (int m = i + 1; m <= j; m++) {
if (boxes[m] == boxes[i]) {
// 把 i 合并到 m 处
dp[i][j][k] = max(dp[i][j][k],
(m - 1 >= i + 1 ? dp[i + 1][m - 1][0] : 0) + dp[m][j][k + 1]);
}
}
}
}
}
return dp[0][n - 1][0];
}
};
这道题实际上给我的感觉难度没有前两道那么变态,但是题目确实是蛮唬人的,而且思路,解法确实很新奇,所以我把这道题目作为本文压轴进行介绍。不瞒大家说,我第一次做这道题的时候直接没看懂题目。这里给大家一个小tips,不要硬生生去读题,读不懂题的时候照着测试用例拿出纸笔画一画,这样能更有助于理解。这里我截取leetcode官方给的一段示例,我们结合着介绍:

这里我们就不再介绍异或运算是怎么求值的了,这里挖个坑,后续我会整理一些位运算相关的题目。注意,题目说的求异或值和我们所说的求异或值不是一个概念。题目的过程分两步:首先对于除最后一个下标以外的所有下标 i,同时将 a[i] 替换为 a[i]⊕a[i + 1] 。然后移除数组中的最后一个元素。我们看一下在第一个查询中子数组[2,8,4]是怎么求的异或值。按照题意,第一次迭代通过[2⊕8,8⊕4]得到[10,12];第二次迭代通过[(2⊕8) XOR (8⊕4)]得到6。同理,对于区间[a,b,c]而言,第一次迭代后会得到[a⊕b, b⊕c],第二次迭代后会得到[a⊕b⊕b⊕c] = [a⊕c]。对于区间[a,b,c,d]而言,第一次迭代后会得到[a⊕b, b⊕c, c⊕d],第二次迭代后会得到[a⊕b⊕b⊕c, b⊕c⊕c⊕d] = [a⊕c, b⊕d],第三次迭代后会得到[a⊕c⊕b⊕d]。通过上面这些例子,我们不难发现每个区间 [i,j] 的最终异或值,可以拆成左半区间和右半区间的异或和。实际上我们就是不断在一个区间上重复的执行操作,这很容易让我们联想到区间DP。我们定义dp[i][j]为每个区间[i,j]的最终异或值,由此我们可以得到一个基础公式dp[i][j] = dp[i][j - 1] ^ dp[i + 1][j]。
经过上面的计算,我们已经求得区间[i,j]的最终异或值了。我们需要明白,dp[i][j] 是区间 [i,j] 经过规定操作后剩下的那个元素,这个值 唯一。换句话说,整个 [i,j] 这个区间最终会“塌缩”为一个元素,这个元素就是 dp[i][j]。因为查询要求的是 任意子数组 的最终异或值最大值,所以我们需要考虑 [i,j] 内所有子数组。我们定义maxdp[i][j]为在区间 [i,j] 上所有子数组的最终异或值中的最大值。我们针对“子数组”这个概念进行讨论,子数组可能是 [i,j] 本身,也可能是 [i+1,j] 或 [i,j-1] 或更短的区间。问题又回到了基于两侧端点可能性展开的区间DP模型。于是我们可以总结出maxdp[i][j]=max(dp[i][j],maxdp[i+1][j],maxdp[i][j-1])。这便是我们这道题的状态转移方程,属于“套娃DP”,很有意思。而“套娃”本质是先求区间状态,再求区间内最大值。这是一种非常难得一见的思路,借鉴了灵神的题解。值得我们学习积累!示例代码如下:
class Solution {
public:
vector<int> maximumSubarrayXor(vector<int>& nums, vector<vector<int>>& queries) {
int n = nums.size();
vector<vector<int>> dp(n, vector<int>(n, 0));
vector<vector<int>> maxdp(n, vector<int>(n, 0));
// 先计算dp[i][j],区间[i,j]的最终异或值
for (int len = 1; len <= n; len++) {
for (int i = 0; i + len - 1 < n; i++) {
int j = i + len - 1;
if (len == 1) {
dp[i][j] = nums[i];
} else {
dp[i][j] = dp[i][j - 1] ^ dp[i + 1][j];
}
}
}
// 计算maxdp[i][j],区间[i,j]所有子数组最终异或值最大值
for (int len = 1; len <= n; len++) { // 枚举区间长度
for (int i = 0; i + len - 1 < n; i++) {
int j = i + len - 1;
if (len == 1) {
maxdp[i][j] = dp[i][j];
} else {
maxdp[i][j] = max({dp[i][j], maxdp[i + 1][j], maxdp[i][j - 1]});
}
}
}
// 处理查询
vector<int> ans;
for (auto &q : queries) {
int l = q[0], r = q[1];
ans.push_back(maxdp[l][r]);
}
return ans;
}
};
以上便是我介绍的并推荐的一些关于区间DP的题目,就题目而言真的是精彩至极,令我大受震撼,几个月后回顾这些题目依旧是回味无穷。但是我的介绍可能也存在问题,有失偏颇,有不当之处还请朋友们多多批评指正,衷心感谢大家的支持和帮助,我们一起进步!





















 505
505

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








