水下传感器3D拓扑设计

一种用于水下传感器网络的新型3D拓扑设计

一、摘要

水下传感器网络对于科学、商业和国防相关应用非常有用，例如海洋数据收集、海洋采样、污染监测、海啸和海底地震预警以及水下监视。对于某些应用（如油田勘探），在海床上进行传感器节点的二维部署已足够。然而，大多数其他指定的水下传感器网络应用局限于三维环境，其中传感器节点被部署在从海底到不同深度的位置。

本文提出了一种针对三维（3D）水下传感器网络的新型拓扑设计。我们的主要目标是制定一种有效的传感器部署策略，以尽可能少的传感器节点数量覆盖有限三维目标区域，同时不忽略边界效应的影响。具体而言，根据传感器节点的感知范围和通信范围，通过分析推导出两个传感器节点之间的最优距离，以确保在三维水下空间中对给定体积的目标区域实现全覆盖，并使用尽可能少的传感器节点。此外，还获得了传感器节点在三维目标区域中的部署坐标。本文描述了该拓扑结构，并在MATLAB上实现了该设计。同时，在实现全覆盖与连通性方面，将所需传感器节点数量和通信范围与现有的相关工作进行了比较。

II. 相关工作

为实现对目标区域的全覆盖和连通性，三维拓扑结构设计是水下传感器网络（UWSN）设计中面临的重要挑战之一[1]。在最近的研究中[2],[3],，针对UWSN的媒体访问控制（MAC）协议提出时，研究重点主要集中在二维拓扑结构上。在[4], 中，作者提出了针对随机部署的UWSN的基于簇的路由协议；在[5],中，作者研究了用于入侵者定位的基于簇的架构，其中传感器节点部署在立方体顶点，簇头位于立方体中心。然而，这些研究[4],[5]未考虑覆盖问题。在[6],[7],中，考虑了传感器节点的随机拓扑结构以覆盖三维目标区域。然而，随机拓扑结构仅适用于

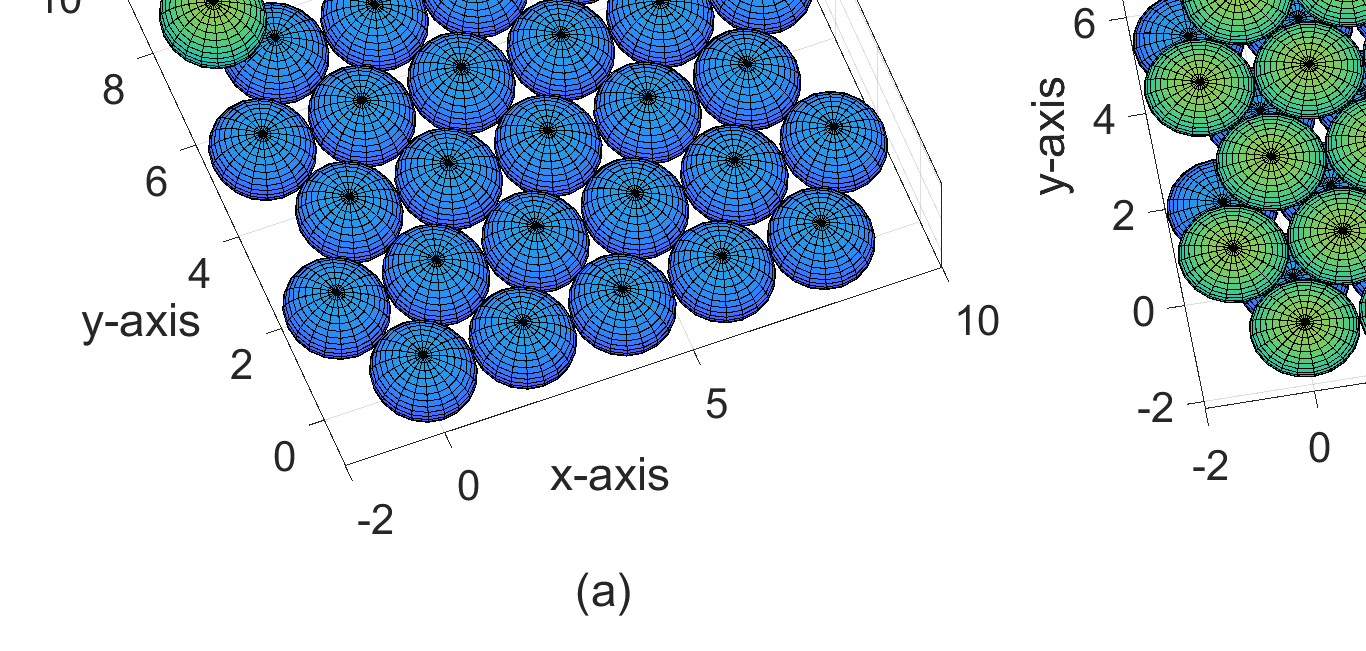一层 (b) 使用 d=2Rs的传感器节点两层部署。)

部署具有大量低成本传感器节点的密集网络以实现全覆盖。

针对高效率且成本较高的传感器节点，已提出一种规则的三维拓扑结构[8]。为了支持该规则三维拓扑结构，需要相对于参考节点进行适当的定位，而先进的定位技术使得这一目标得以实现[9],[10]。在本研究中，提出了一种新的规则三维拓扑结构，旨在用最少数量的传感器节点完全覆盖目标三维区域，并将结果与最突出的相关工作进行比较[8]。

III. 所提出的拓扑结构

通过使用某些多面体的集合，可以对整个三维空间进行铺砌，这类多面体的示例包括：立方体、六角柱、菱形十二面体和截断八面体。在本研究中，考虑到所有传感器节点通常采用基于球形的均匀感知模型和全向球形通信模型，这在水下传感器网络部署中是一般情况，因此采用球形代替多面体。设 Rs 和 Rc 分别表示所有传感器节点的感知范围和通信范围。众所周知，六边形结构是二维空间中最优的空间填充方式，因此第一层的传感器节点基于三角网格结构排列，形成如图1(a)所示的六边形形状。设

d = 2Rs 表示两个相邻传感器节点之间的距离，换句话说，即为连接各中心点所形成的等边三角形的边长

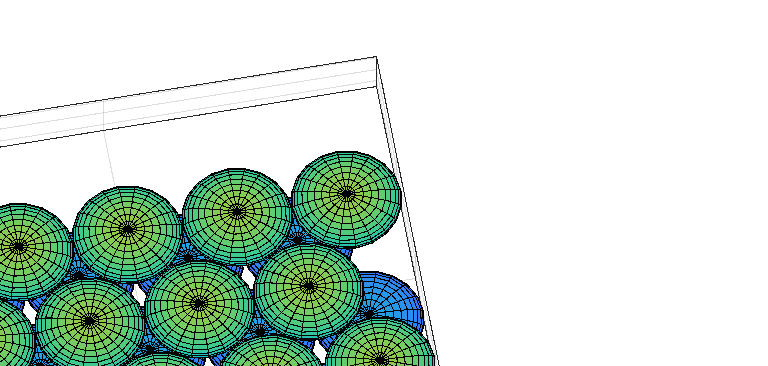
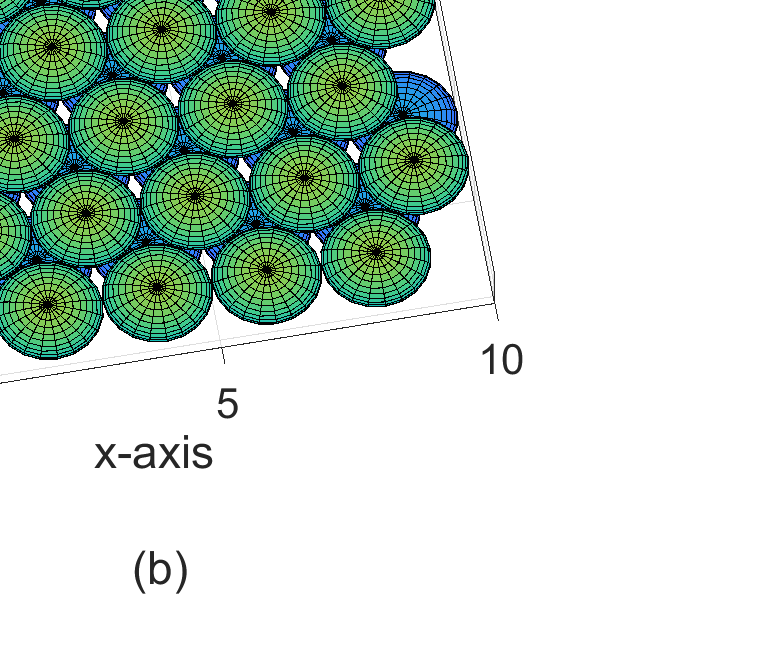使用 d= 2Rs进行传感器节点的三层部署。(b) 图2(a)的侧视图，显示覆盖空洞。)

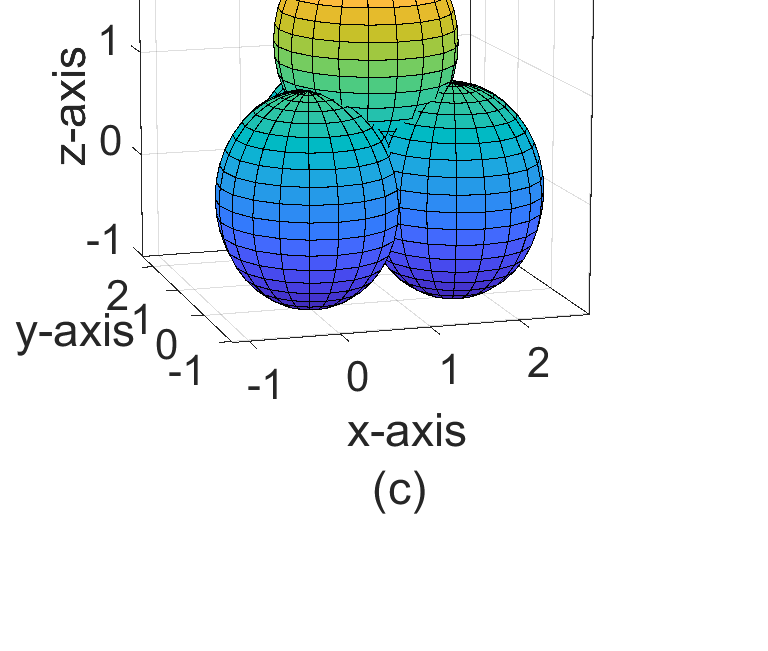
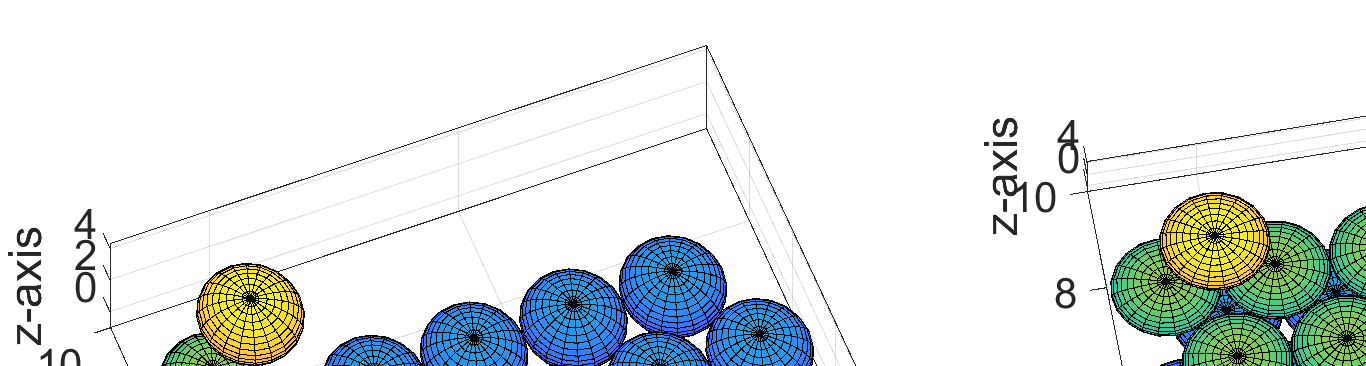具有 d= 2Rs的非零四面体空隙 (b) 四面体与球体的交集 (c) 具有 d= dopt的零空隙)

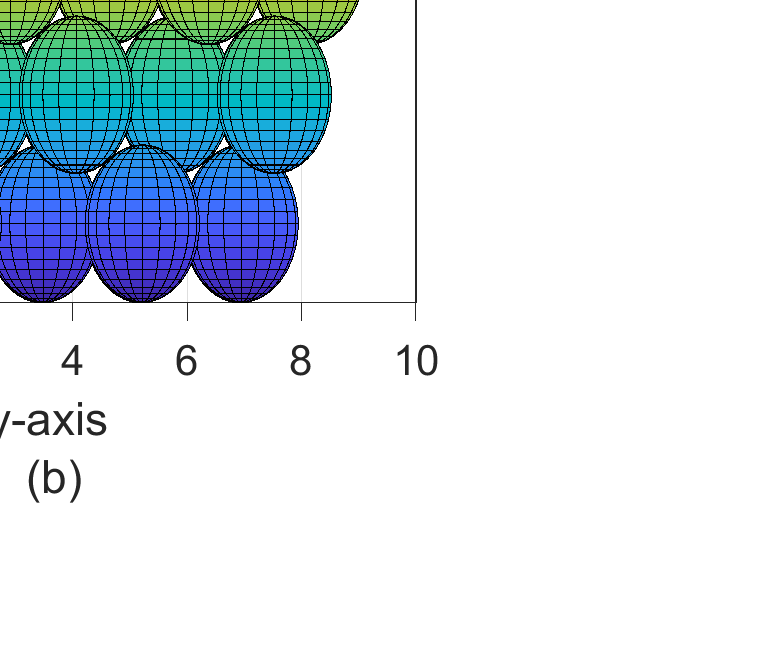
三个相切的球体。注意，每个球体的中心代表每个传感器节点的位置，半径为 Rs 的完整球体表示该传感器节点所覆盖/感知的区域。第二层放置在第一层中交替的四面体空隙上，如图1(b)所示，第三层放置在第二层的八面体空隙上，如图2(a)所示。请注意，这种拓扑结构可以从上至下方向检测对目标三维区域的入侵，但在水平方向存在覆盖空洞，如图2(a)的侧视图（图2(b)）所示。在下一小节中，将通过解析方法推导相邻传感器节点之间的最优距离，使得这些覆盖空洞消失，从而用尽可能少的传感器节点数量实现对三维目标区域的全覆盖。

A. 传感器节点间的最优距离（dopt）

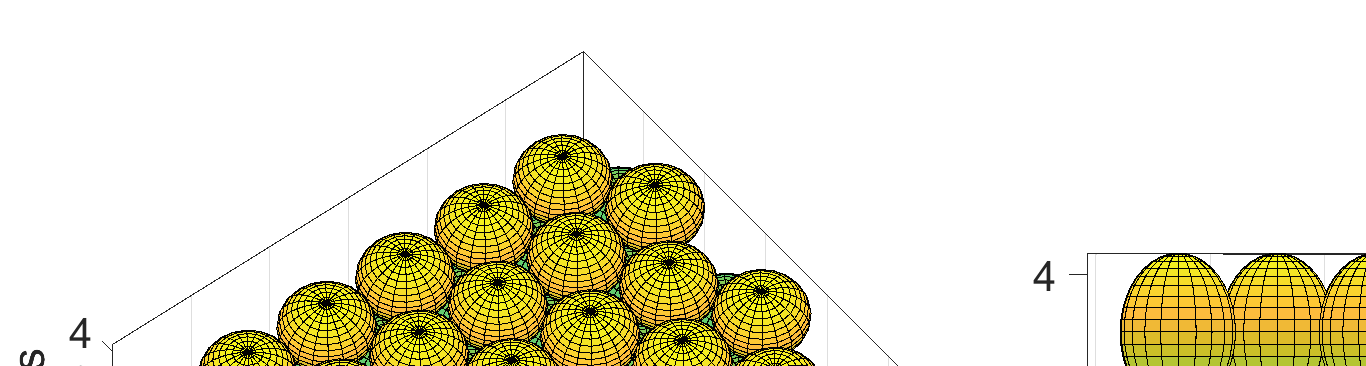
为了填补图2(b)中所示的覆盖空洞（这些覆盖空洞是由于图3(a)中所示的四面体空隙在拓扑结构中产生的），节点之间的距离 d 被减小至其最优值 dopt，使得该空隙可以如图3(c)所示被完全消除。通过将传感器节点之间的距离减小至等于 dopt 的值，可以在使用尽可能少数量的高质量且昂贵的传感器节点的同时，实现对整个目标区域的覆盖。

如果将虚拟四面体视为如图3(b)所示，它由同一层内三个相切球体的中心与第四个相切球体的中心连接而成

无论是在上层还是下层（在图3中，第四个球体被视为来自上层）。该四面体空隙导致了目标区域中的覆盖空洞。现在通过计算四面体空隙的体积来评估未覆盖区域的体积。

根据我们所提出的拓扑结构，如图3(b)所示，虚拟四面体的一条边等于两个相邻传感器节点之间的距离 d = 2Rs。

从图3(a)和图3(b)可以看出，空隙区域的体积明显小于上述等边四面体的体积。图4和图5展示了半径为 Rs 的球体内所包含的四面体体积的比例。首先，我们使用图6所示的球坐标系，计算如图4所示的四面体在球体内的区域体积。设 (VT)s 表示该体积，则将四面体与球体的交集体积分成两部分进行计算：其中一部分当 φ 从 0 变化到 π/6 弧度时，角度 θ 从 0 变化到 π/3 弧度，因此这两个角度变化之间的关系为 φ = θ/2，体积(VT)s 的计算如下：

$$
(VT) s = 2 \int {\theta=0}^{\pi/3} \int_{\phi=0}^{\theta/2} \int_{r=0}^{R_s} r^2 \cos\theta \, dr \, d\phi \, d\theta
= \frac{2R_s^3}{3} \int_{0}^{\pi/3} \frac{\theta}{2} \cos\theta \, d\theta
= \frac{R_s^3}{3}\left[ \frac{\pi}{2\sqrt{3}} - \frac{1}{2} \right] \quad (1)
$$

上述考虑的虚拟四面体的总体积由 d = 2Rs 给出

$$
V_T = \frac{d^3}{6\sqrt{2}} = \frac{8R_s^3}{6\sqrt{2}} = \frac{4R_s^3}{3\sqrt{2}} \quad (2)
$$

现在，图3(a)中所示的空洞区域（覆盖空洞）的体积 VH 为

$$
V_H = V_T - 4(V_T)_s
= \frac{4R_s^3}{3\sqrt{2}} - \frac{4R_s^3}{3}\left[ \frac{\pi}{2\sqrt{3}} - \frac{1}{2} \right] \quad (3)
= \frac{4R_s^3}{3}\left[ \frac{1}{\sqrt{2}} - \frac{\pi}{2\sqrt{3}} + \frac{1}{2} \right] \quad (4)
$$

现在，如果四个传感器节点的感知范围都包含或接触到该虚拟四面体的中心，则可消除导致覆盖空洞的四面体空隙。换句话说，每个顶点（即传感器节点的位置）到虚拟四面体的中心的距离应小于或等于传感器节点的感知范围。

为了获得此距离，从每个顶点向对侧等边三角形的内心作长度为 h 的垂线，如图7所示。这四条垂线共点，相交于一个称为四面体的中心的公共点。四面体的中心将垂线分为 3:1 的比例。因此，每个顶点与四面体的中心之间的距离 dVC 表示如下：

$$
d_{VC} = \frac{3}{4} \times h \quad (5)
$$

由于此处形成的虚拟四面体是等边的，垂线的长度将与四面体的高相同

hedron，可根据图8计算如下：令 a = d

$$
h = \sqrt{d^2 - \left( \frac{d}{\sqrt{3}} \right)^2} = \sqrt{\frac{2}{3}} d \quad (6)
$$

将 h 的值代入公式(5)，得到

$$
d_{VC} = \frac{3}{4} \times h
= \frac{3}{4} \times \sqrt{\frac{2}{3}} d
= \frac{\sqrt{6}}{4} d \quad (7)
$$

现在，如果每个顶点与虚拟四面体中心之间的距离 dVC 小于节点的感知范围，则四面体空隙可以被完全覆盖，这可以用数学方式表示如下：

$$
d_{VC} \leq R_s \quad (8)
$$

$$
\frac{\sqrt{6}}{4} d \leq R_s \quad (9)
$$

$$
d \leq \frac{4}{\sqrt{6}} R_s = 2\sqrt{\frac{2}{3}} R_s \quad (10)
$$

因此，两个传感器节点之间的最优距离 dopt 为

$$
d_{opt} = 2\sqrt{\frac{2}{3}} R_s
$$

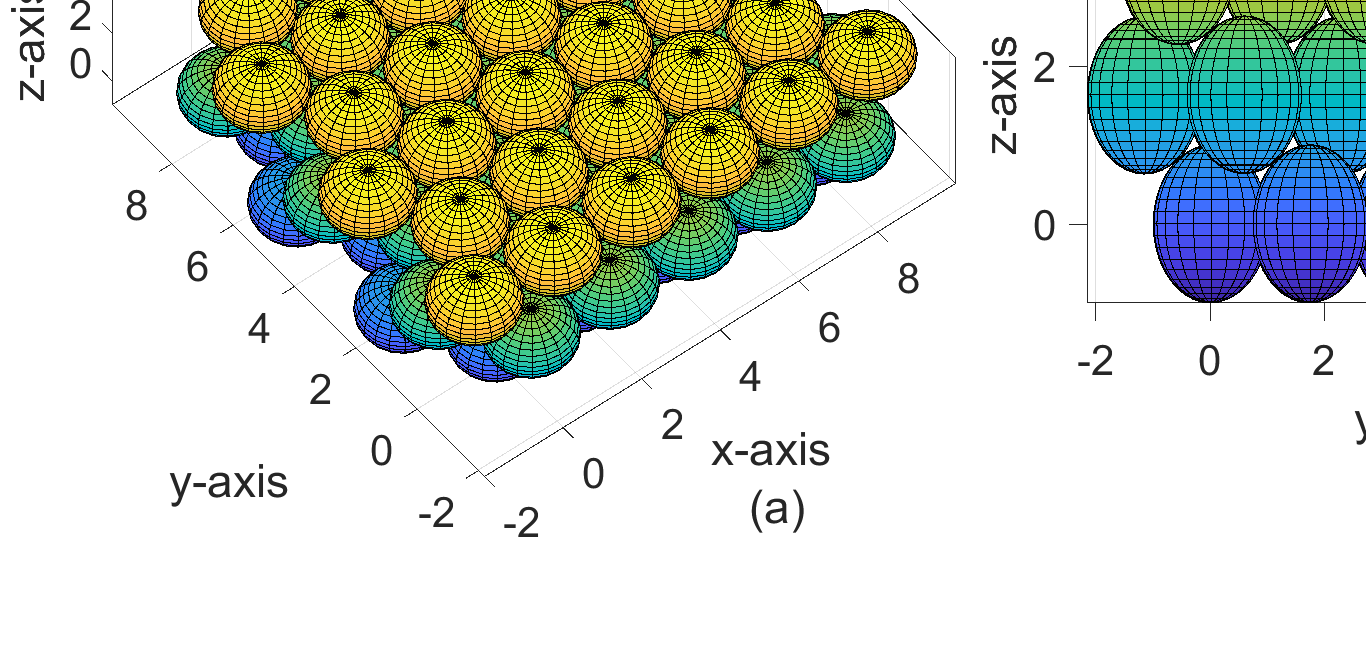
这填补了拓扑结构中的四面体空隙，如图3(c)所示，并确保在三维水下空间中以尽可能少的传感器节点数量实现对给定目标区域的全覆盖。图9(a)表示在三维区域中使用MATLAB实现所提出的拓扑结构的三层部署，d = dopt。从图9(b)中拓扑结构的侧视图可以看出，当前拓扑结构中已不存在覆盖空洞，整个三维目标区域均可被覆盖。在下一小节中，将给出传感器节点在三维目标区域中的部署坐标。

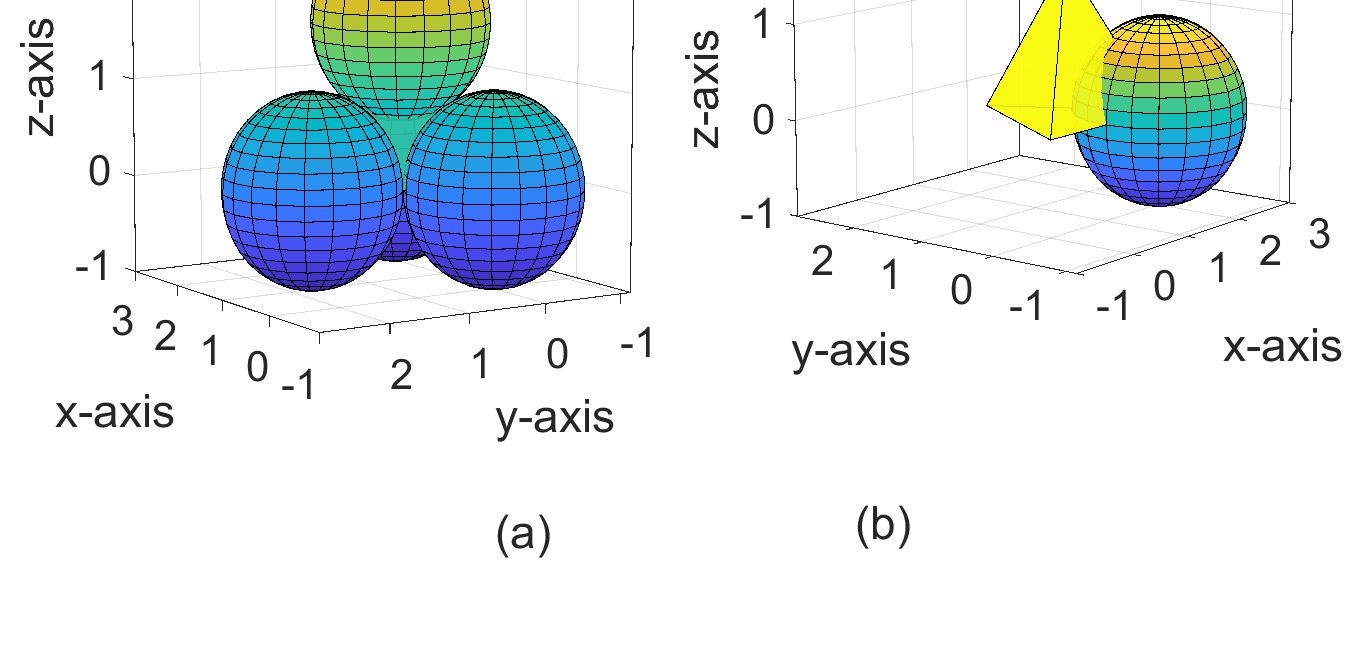使用 d= dopt进行传感器节点的三层部署。(b) 图9(a)的侧视图，显示无覆盖空洞。)

B. 传感器节点的部署坐标

考虑一个有限的三维水下目标区域，其尺寸为 $ X \times Y \times Z $，以笛卡尔坐标表示。为了在二维平面上水平覆盖该空间，传感器节点按照三角形网格结构进行布置，如图1(a)所示。因此，沿x轴每增加一个传感器节点，其坐标在x轴方向移动距离 $ dx $，其中

$$
dx = d_{opt} = 2\sqrt{\frac{2}{3}} R_s \quad (11)
$$

根据目标区域的x轴维度，即 $ X $，沿x轴所需的最少传感器节点数量为：

$$
x_n = \left\lceil \frac{X}{d_{opt}} \right\rceil + 1 \quad (12)
$$

注意，在 $ \left\lceil \frac{X}{d_{opt}} \right\rceil + 1 $ 个传感器节点中，额外增加了一个传感器节点以考虑目标区域的边界效应。在第一下层中，传感器节点按照三角网格结构布置在目标区域的边界上，形成如图1(a)所示的六边形，且满足 $ d = d_{opt} $，使得即使由于海浪洋流导致传感器节点发生移动，目标区域仍处于传感器节点的感知范围内，且该移动可在距离 $ R_s/2 $ 内被容忍。

在上层中，同样根据所提出的布放策略，传感器节点布置在三维目标区域体积的边界上。

在三角形网格结构中，如果 $ d_{opt} $ 是等边三角形每条边的长度，则y轴上的坐标偏移 $ dy $ 将为

$$
dy = \sqrt{d_{opt}^2 - \left(\frac{d_{opt}}{2}\right)^2}
= \frac{\sqrt{3}}{2} d_{opt} = \sqrt{2} R_s \quad (13)
$$

因此，沿y轴所需的层数 $ y_n $ 表示为

$$
y_n = \left\lceil \frac{Y}{dy} \right\rceil + 1 \quad (14)
$$

现在沿着z轴，传感器节点被放置以覆盖下层的交替四面体空隙。因此，传感器节点到下层的高度将等于从虚拟四面体中顶点到对侧等边三角形中心所作垂线的长度，即

$$
dz = \sqrt{\frac{2}{3}} d_{opt} = \frac{4}{3} R_s \quad (15)
$$

因此，根据目标区域的维度，沿z轴方向的传感器节点层数 $ z_n $ 将为

$$
z_n = \left\lceil \frac{Z}{dz} \right\rceil + 1 \quad (16)
$$

在该拓扑结构中，第一水平层中最底层的传感器节点沿x轴和y轴遵循基于三角形网格的部署方式。随后，在z轴方向上的第二水平层中，传感器节点被放置在第一层的交替四面体空隙上方。在第三层及以上各层中，传感器节点被放置在其下层的八面体空隙上方。因此，前三层中传感器节点的水平坐标各不相同。在第三层之后，第四层的传感器节点水平坐标将与第一层的传感器节点水平坐标相同，仅z轴坐标因高度不同而有所差异。进一步地，第五层的水平坐标将与第二层的水平坐标一致，第六层的水平坐标将与第三层的水平坐标一致。通常情况下，若 $ L $ 为沿z轴的层数，则当 $ \text{rem}(L,3) = 1 $ 时，其水平坐标与第一层的水平坐标相同；当 $ \text{rem}(L,3) = 2 $ 时，其水平坐标与第二层的水平坐标相同；当 $ \text{rem}(L,3) = 0 $ 时，其水平坐标与第三层的水平坐标相同。图10表示了所提出的拓扑结构中传感器节点的部署情况，该部署基于上述笛卡尔坐标，覆盖三维空间中的较大目标区域。

C. 覆盖与连通性

我们通过分析计算得出，当每个传感器节点的感知范围为 $ R_s $ 时，两个节点之间的最优距离为 $ d_{opt} = 2\sqrt{\frac{2}{3}} R_s $，以用尽可能少的数量的传感器节点覆盖整个目标区域。在此场景中，为了与所有12个最近邻节点（即同一平面内的6个节点、上层平面的3个节点和下层平面的3个节点）进行通信，通信范围 $ R_c $ 应大于或至少等于 $ d_{opt} $，即

$$
R_c \geq d_{opt}
= 2\sqrt{\frac{2}{3}} R_s
= 1.6330 R_s \quad (17)
$$

因此，传感器节点的通信范围 $ R_c $ 与感知范围 $ R_s $ 所需的比率为

$$
\frac{R_c}{R_s} \geq 1.6330 \quad (18)
$$

而在基于截断八面体镶嵌的拓扑结构中，[8]提供的最佳结果仅为与六个节点通信。因此，在所提出的拓扑结构中，连通性是截断八面体拓扑在[8]且传感器节点通信范围仅需截断八面体拓扑中传感器节点的 $ \frac{1.6330}{1.7888} = 0.9129 $ 倍时的两倍。同时声称，所需传感器节点数量比基于截断八面体镶嵌的拓扑结构所需的传感器节点数量少7.05%。该声明的证明如下：[8]

对于所提出的拓扑结构，基于笛卡尔坐标的虚拟立方体体积为

$$
d_{opt} \times dy \times dz = 2\sqrt{\frac{2}{3}} R_s \times \sqrt{2} R_s \times \frac{4}{3} R_s = 3.0792 R_s^3
$$

根据在[8]中定义的基于截断八面体拓扑的传感器节点部署策略，一个基于笛卡尔坐标的虚拟立方体体积为

$$
\frac{4}{\sqrt{5}} R_s \times \frac{4}{\sqrt{5}} R_s \times \frac{2}{\sqrt{5}} R_s = 2.8622 R_s^3
$$

对于基于菱形十二面体的拓扑，一个虚拟立方体的体积为

$$
\sqrt{2} R_s \times \sqrt{2} R_s \times R_s = 2 R_s^3
$$

对于基于六角柱的拓扑，一个虚拟立方体的体积为

$$
\frac{\sqrt{3}}{2} R_s \times \sqrt{2} R_s \times \frac{2}{\sqrt{3}} R_s = 2 R_s^3
$$

而对于基于立方体的拓扑，一个虚拟立方体的体积为

$$
\frac{2}{\sqrt{3}} R_s \times \frac{2}{\sqrt{3}} R_s \times \frac{2}{\sqrt{3}} R_s = 1.5396 R_s^3
$$

现在，为了覆盖目标区域，相对于基于截断八面体的拓扑结构，给定拓扑所需的相对节点数量通过其各自虚拟立方体体积的比率计算得出。例如，对于基于菱形十二面体和六角柱的拓扑，相对于基于截断八面体的拓扑所需的相对节点数量为

$$
\frac{2.8622 R_s^3}{2 R_s^3} \times 100 = 143.11\%
$$

对于基于立方体的拓扑，所需相对节点数量为

$$
\frac{2.8622 R_s^3}{1.5396 R_s^3} \times 100 = 185.91\%
$$

这些结果与[8]中提供的结果一致。类似地，所提出的拓扑相对于基于截断八面体的拓扑所需的相对节点数量为

$$
\frac{2.8622 R_s^3}{3.0792 R_s^3} \times 100 = 92.95\%
$$

因此，在所提出的拓扑结构中所需的传感器节点数量比基于截断八面体镶嵌的拓扑结构少7.05%。

IV. 结论

本文提出了一种用于三维（3D）水下传感器网络的新颖拓扑设计。为了用最少数量的传感器节点覆盖有限三维目标区域，计算了相邻传感器节点之间的最优距离 $ d_{opt} $，该距离取决于传感器节点的感知范围。此外，提供了传感器节点的笛卡尔坐标和部署策略，同时确保覆盖三维目标区域的边界。还计算了传感器节点的通信范围与感知范围的比率，以实现传感器网络的连通性。在实现全覆盖与连通性方面，从所需的传感器节点数量和通信范围两个角度，将结果与现有相关工作中针对三维目标区域的最佳拓扑（即截断八面体）进行了比较。所提出的拓扑结构在提供双重连通性的同时，所需的传感器节点通信范围减少了8.71%，并且在实现三维目标区域全覆盖的情况下，所需传感器节点数量比基于截断八面体的拓扑结构减少了7.05%。