基于CNN-LSTM的波浪预测

基于CNN‐LSTM的波浪高度预测

摘要

短期波浪高度预报对能源的开发利用具有重要意义。为了提高短期波浪高度预测的准确性，本文提出了一种基于卷积神经网络（CNN）和长短期记忆（LSTM）网络的预测模型，该模型具有优异的特征提取能力，并且非常擅长处理时间序列数据。该模型利用卷积神经网络对最大波高（Hmax）、零上穿波浪周期（Tz）、峰值能量波浪周期（Tp）、来自真实北向的峰值周期波浪方向（Dir_Tp_TRUE）以及海表温度（SST）近似数据进行卷积和池化计算，以提取波高相关数据的特征图。为了描述波高序列的时间依赖性，将谱特征信息作为LSTM网络的输入信息，以计算波高预测结果。我们采用澳大利亚的实际测量数据验证了该模型的准确性，实验结果表明，该模型相较于LSTM、支持向量机（SVM）、随机森林（RF）等其他机器学习模型具有更好的预测性能。

关键词 ：时间序列；卷积神经网络；长短期记忆网络；特征提取；深度学习；波浪高度预测

I. 引言

二氧化碳水平的上升以及随之而来的全球平均气温升高，加之可再生能源的快速消耗，推动了环保和可再生能源技术的发展。水电、太阳能和风能技术已较为成熟且合理，但海洋可再生能源的发展相对滞后[1]。在澳大利亚，这个被广阔海洋环绕的“岛大陆”拥有巨大的波浪能潜力。澳大利亚的主要优势在于，丰富的波浪能资源距离家庭和潜在工业区较近，能够实现经济高效的电力传输。此外，与风能相比，波浪能具有更高的确定性和一致性[2]。然而，波浪是一种受自然混沌行为控制的变动能源。因此，有必要通过适当的预测方法对该间歇性能源进行深入研究，以评估其用于可持续发电的可用性和可靠性。需要预测的关键波浪参数之一是有效波高（HS）。HS用于描述波浪状况，而对HS的极短期预测对于发电[3], 海洋工程目的、提高海洋活动的安全性和效率[4], 以及海岸灾害风险管理至关重要。波浪能水平与HS直接相关，是波浪能发电的关键参数[5]。为了模拟有效波高（HS）的预测已开发出许多使用数据智能方法的预测模型。然而，这些研究仍处于初级阶段。在波浪参数预测中探索的算法包括分类与回归树的C5算法[6], M5树模型[7], 人工神经网络（ANN）[6][8], 支持向量机（SVM）[8][9], 基于自适应网络的模糊推理系统（ANFIS）[9][10]。

夸德拉，萨莱多·桑兹[11]综述了计算智能在波浪能应用中的应用，发现人工神经网络是一种广泛应用且性能优于回归模型的模型。然而，这些均为经典的独立模型，可能无法充分捕捉随机波浪的非线性动力学特性。

在海岸与海洋工程的应用和预测中，最具价值的挑战之一是处理时间序列中非平稳和非线性波浪的自然随机性。非平稳特征导致序列中存在非正态性、双峰、不对称周期和非线性。为了应对非平稳特征，有必要对每个数据驱动模型的输入进行适当的预处理[12][13]。因此，采用多分辨率分析（MRA）[16][17]工具来揭示嵌入的函数，以克服非平稳性问题。

考虑到卷积神经网络具有出色的数据特征提取能力[14][18]，而长短期记忆网络在描述时间序列的长期依赖性以及波浪高度预测的广泛应用方面表现优异[20]，本文提出了一种基于CNN‐LSTM的短期波高预测模型。该模型结合了卷积神经网络和LSTM网络各自的优势，利用卷积神经网络中的卷积层和池化层对波高相关数据进行特征信息提取。在此基础上，将冗余数据较少的特征信息作为LSTM网络的输入，以提取波高特征序列的时间耦合关系，进而得到波高预测结果。现场实测数据验证表明，该模型相较于普通的LSTM和随机森林模型具有更好的预测性能。

II. 相关理论研究

深度神经网络是深度学习的一个重要分支。它通过构建更复杂的网络结构来提升特征提取能力。与传统神经网络相比，深度神经网络通过多个隐藏层进行非线性变化，更容易应对复杂环境和问题。

A. 卷积神经网络

卷积神经网络是一种深度神经网络。其结构更为复杂，通常由输入层、卷积层、池化层、全连接层和输出层等[15]。本文主要使用卷积层和池化层从波高相关数据中提取特征。该二维卷积层的结构如图1所示。

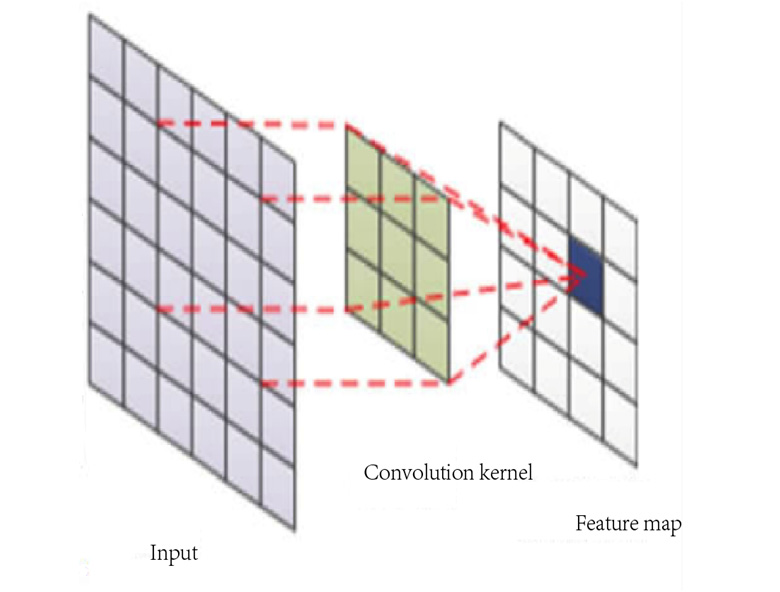
计算过程如公式(1)所示：

$$
Y_{jk} = f\left(\sum_{i \in N_j} x_{ik-1} u_{ijk} + b_{jk}\right) \tag{1}
$$

其中：$x_{ik-1}$ 是第 $(k-1)$ 层第 $i$ 个特征图的输出值；$u_{ijk}$ 是第 $k$ 层第 $j$ 个特征图与第 $(k-1)$ 层第 $i$ 个特征图之间的卷积核；$b_{jk}$ 是第 $k$ 层第 $j$ 个特征图对应的阈值；$N_j$ 是输入特征图的集合；$Y_{jk}$ 是第 $k$ 层第 $j$ 个特征图的输出值；$f(\cdot)$ 是激活函数。

卷积层设置卷积核的大小和步长进行移动，对输入数据执行卷积操作以获得特征图。通常，有多个卷积核用于提取输入信号的不同特征信息，并得到多个特征图。池化层是一种非线性下采样形式。最大池化是取邻域[19]内特征点的最大值。本文采用最大池化方法对数据进行降维，以减少参数数量和网络复杂度。通常，多个卷积层和池化层交替连接，逐层提取特征。随着卷积层和池化层的堆叠，将逐步提取输入信息的深层特征[20]。

B. 长短期记忆网络

LSTM记忆单元的结构如图2所示。

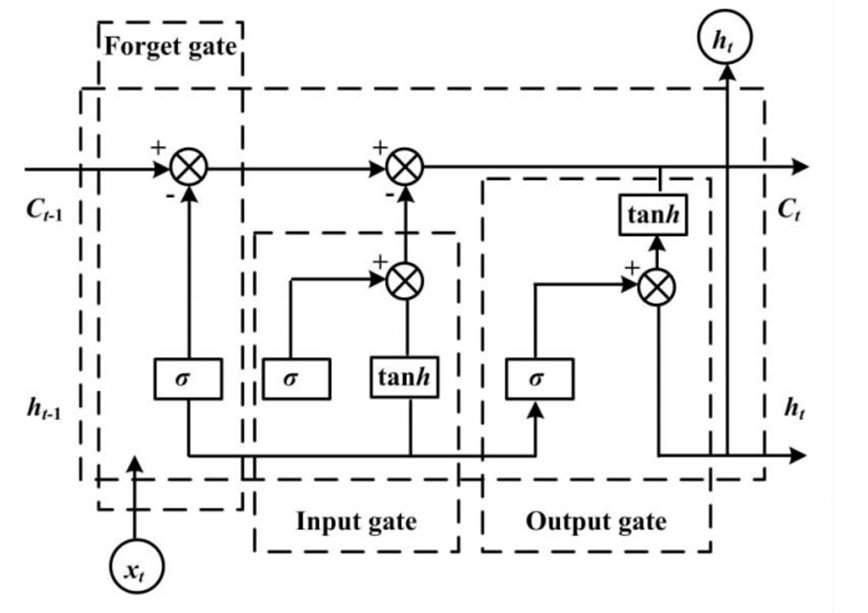
LSTM网络隐藏层的信息传递过程如图3所示。

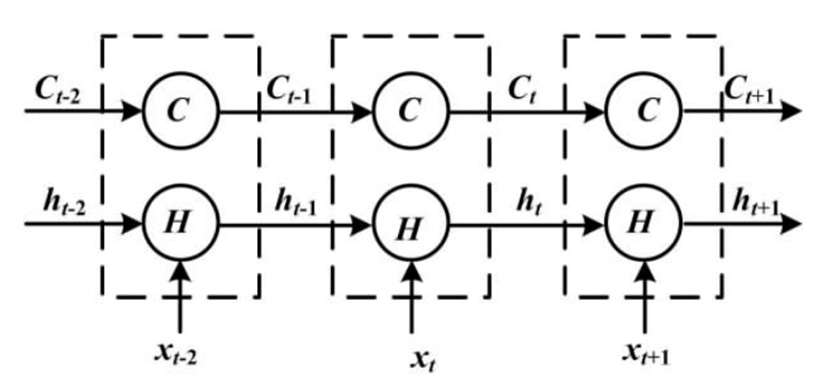
LSTM网络通过在隐藏层中添加遗忘门、输入门和输出门，能够有效挖掘时间序列中信息的时间依赖性。

在每个时刻，长短期记忆网络单元通过三个门接收当前数据$x_t$以及上一个隐藏状态$h_{t-1}$和记忆单元状态$C_{t-1}$。然后，长短期记忆网络的计算过程如下。

遗忘门有助于长短期记忆网络决定哪些信息将被存储在记忆单元中：

$$
f_t = \sigma(W_{fx}x_t + W_{fh}h_{t-1} + b_f) \tag{2}
$$

长短期记忆网络使用输入门来决定哪些数据将存储在新单元中。状态$C_t$的新信息计算如下：

$$
i_t = \sigma(W_{ix}x_t + W_{ih}h_{t-1} + b_i) \tag{3}
$$
$$
g_t = \phi(W_{gx}x_t + W_{gh}h_{t-1} + b_g) \tag{4}
$$
$$
C_t = C_{t-1} \odot f_t + g_t \odot i_t \tag{5}
$$

其中：$g_t$ 是添加到新细胞状态的候选值；$C_{t-1} \odot f_t$ 用于确定从$C_{t-1}$中遗忘多少信息；$g_t \odot i_t$ 决定有多少信息被添加到新的细胞状态。$C_t$ 是向量乘法中的按位元素。

使用输出门$o_t$计算$h_t$的过程如下：

$$
o_t = \sigma(W_{ox}x_t + W_{oh}h_{t-1} + b_o) \tag{6}
$$
$$
h_t = o_t \phi(C_t) \tag{7}
$$

其中：$\sigma$和$\phi$分别为sigmoid激活函数和tanh激活函数；$W_{fx}, W_{gx}, W_{fh}, W_{ix}, W_{ih}, W_{gx}, W_{ox}, W_{oh}$、$x_t$、$h_{t-1}$、$b_f$、$b_t$、$b_g$、$b_o$分别为遗忘门、输入门、输入节点、输出门与输入$x_t$及上一时刻隐藏状态$h_{t-1}$相乘的权重矩阵；$b_f$、$b_t$、$b_g$、$b_o$为对应的偏置；$f_t$、$i_t$、$g_t$、$o_t$、$C_t$、$h_t$分别为遗忘门、输入门、输入节点、输出门、记忆细胞状态和隐藏状态的输出结果。

III. 基于CNN‐LSTM的短期波高预测

A. 数据特征提取

卷积神经网络的特征提取如图4所示。

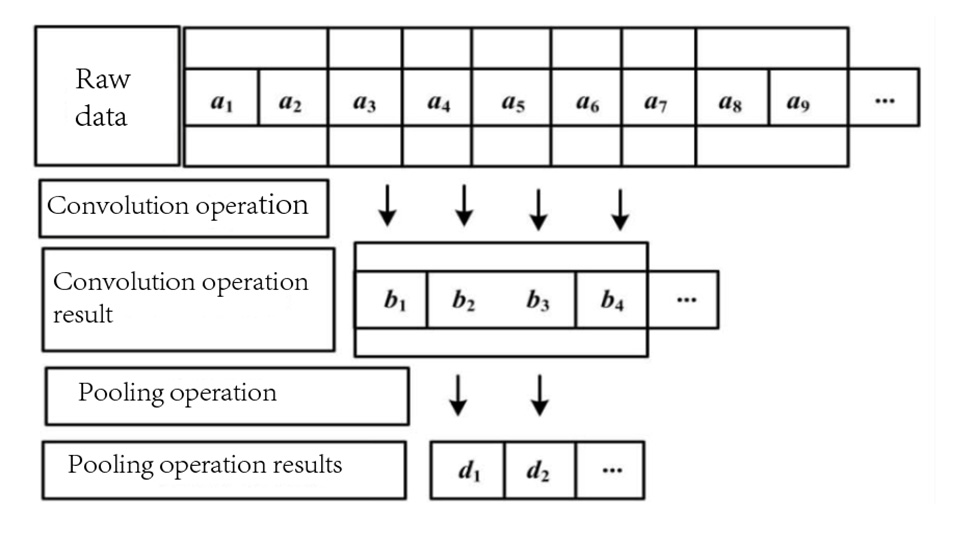
最大波高、零上穿波浪周期、峰值能量波浪周期、来自真北方向的波浪主周期来向、海表温度近似值以及其他因素将影响波高的变化。本文利用2011年至2018[22]年间由昆士兰政府环境与科学部澳大利亚昆士兰州沿海数据系统获取的黄金海岸有效波高数据（单位：米）进行实验。在各个观测点，通过波浪监测浮标以每半小时间隔采集有效波高数据，随后将数据送入卷积神经网络进行特征提取。

本文中，我们首先在预测模型的顶部设置一个一维卷积神经网络，用于提取时间序列向量（Hmax, Tz, Tp, SST, Dir_Tp_TRUE）的隐含特征。如图4所示，a为输入模型的Hmax、Tz、Tp、SST、Dir_Tp_TRUE列向量，大小为1×5，步长为2，卷积核向右移动，经过卷积操作后得到b。通过最大池化方法（池化层大小为1×2）得到特征图d。经过多次堆叠卷积层和池化层后，所获得的特征信息的数据维度已得到一定程度的降低。该信息携带了更清晰反映波高变化的相关数据特征，有利于提高长短期记忆网络模型的学习效率和预测精度。

B. 波高预测过程

CNN‐LSTM的算法流程如图5所示。

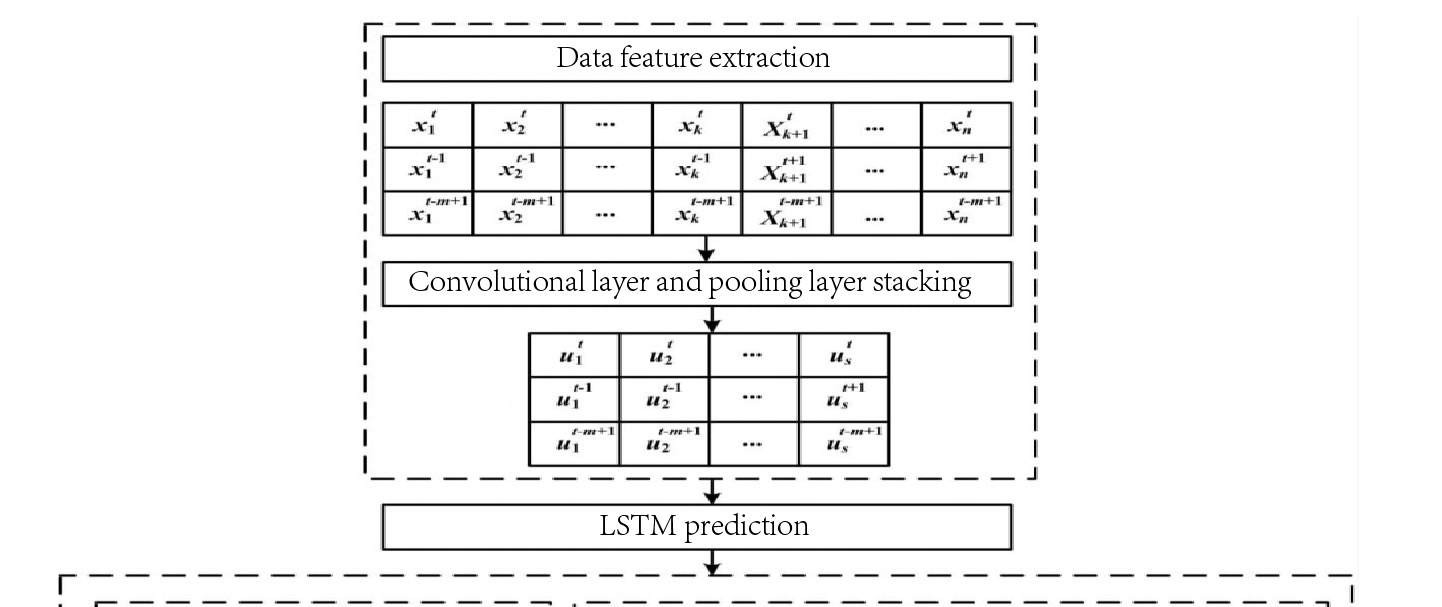
从图5可以看出，CNN‐LSTM短期波高预测模型主要由两部分组成：卷积神经网络从原始时间序列中提取特征信息序列，LSTM网络对获得的特征信息序列进行预测。与传统神经网络不同，LSTM网络在隐藏层中设有记忆单元，(t-1)时刻的隐藏层信息将分别通过隐藏层中的记忆单元H和C传递到t时刻的隐藏层神经元，从而描述时间序列之间的长期相关性。

CNN‐LSTM短期波高预测模型的训练主要经过前向传播和反向传播两个过程。前向传播的主要目的是计算目标损失函数的误差，损失函数的数学公式如公式(8)所示。在反向传播过程中，采用自适应矩估计算法Adam来调整网络参数[21]。

$$
L = \frac{1}{F} \sum_{T=1}^{F} (y_T - \hat{y}_T)^2 \tag{8}
$$

其中：$y_T$为T时刻波高的真实值；$\hat{y}_T$为T时刻波高的预测值；F为训练样本集中的样本数量。

C. 预测评价指标

我们使用均方根误差(RMSE)、平均误差(MAE)和R2决定系数来评价预测结果。RMSE、平均绝对误差和R2的数学公式如下：

$$
RMSE = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (y_i - \hat{y} i)^2} \tag{9}
$$
$$
MAE = \frac{1}{N} \sum {i=1}^{N} |y_i - \hat{y} i| \tag{10}
$$
$$
R^2(y,\hat{y}) = \frac{\sum {i=0}^{n-1} (y_i - \hat{y} i)^2}{\sum {i=0}^{n-1} (y_i - \bar{y})^2} \tag{11}
$$

其中：$\hat{y}_i$ 是第 $i$ 个测试样本的预测值；$y_i$ 是第 $i$ 个测试样本的实际值；$\bar{y}$ 是平均值；N 是测试样本的数量。

IV. 实验分析与对比

A. 模型参数选择

在CNN‐LSTM模型中，本文构建的模型中，卷积神经网络负责原始数据特征提取，LSTM网络负责波浪高度预测。通过测试调优，采用一个卷积层和一个池化层来提取数据序列的特征。第一层有64个卷积核，大小为1×1，步长设置为1，池化层大小为1×5。

考虑到固定卷积层和池化层中提取的特征信息不变，当LSTM的隐藏层为64个单元，且批量大小为256时，模型表现出最优的收敛性和预测性能。

B. 测试结果分析

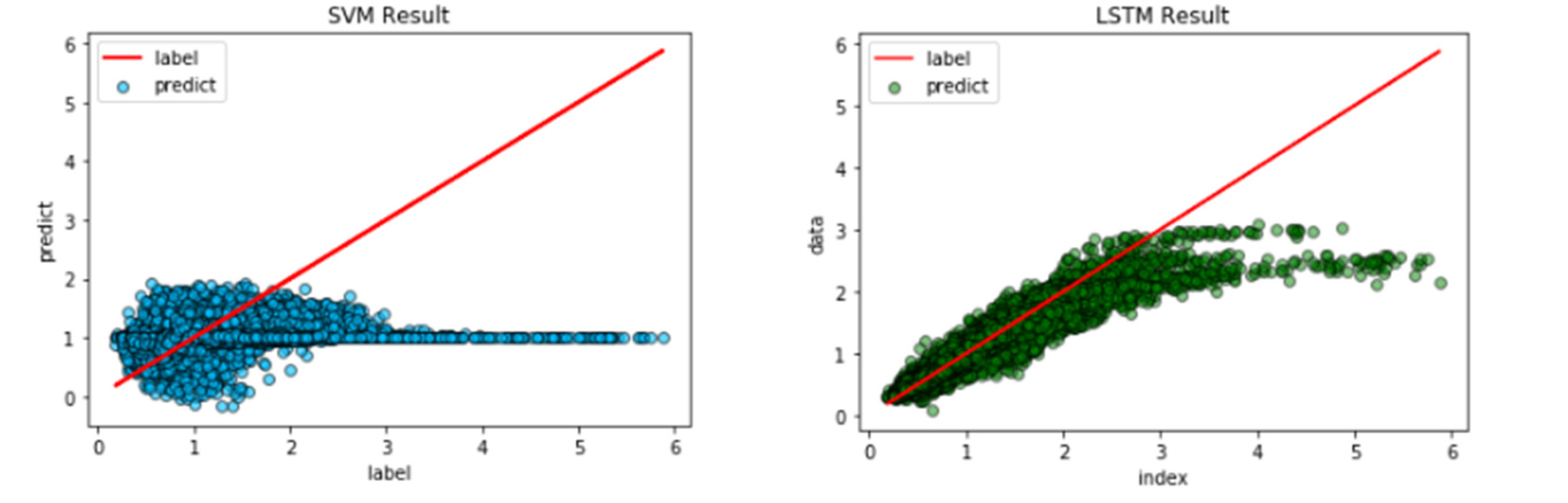
各模型的预测结果如图6和图7所示。

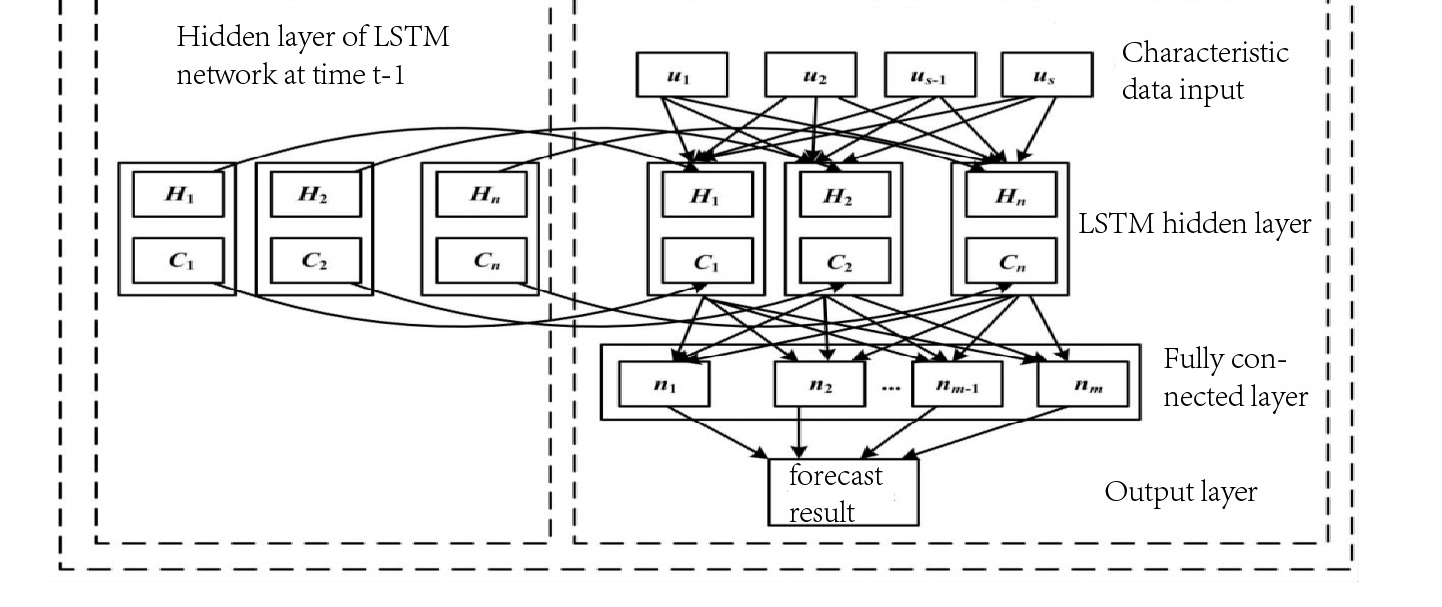
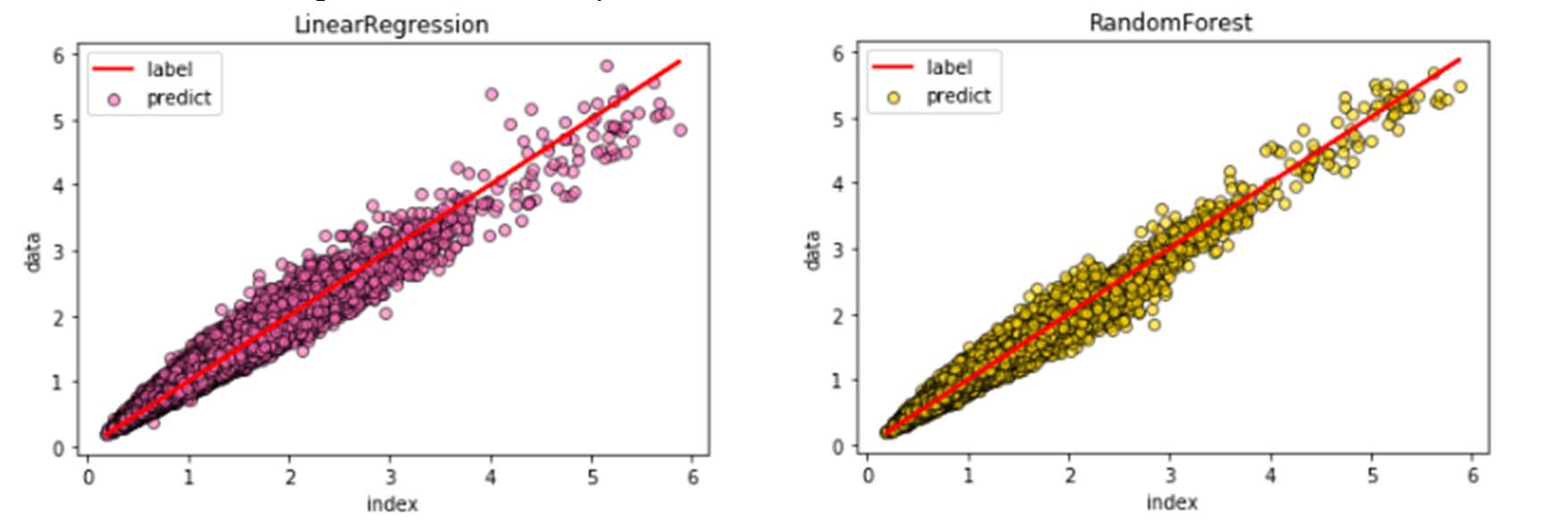
在确定CNN‐LSTM模型的网络结构和超参数后，为了验证所提出模型的预测性能，本文采用CNN‐LSTM模型、SVM、RF、线性回归和LSTM网络对波高进行预测。预测误差分析见表1。

模型	评价指标	指标值
CNN‐LSTM	RMSE	0.0103
	MAE	0.0077
	R²	0.9952
LSTM	RMSE	0.1286
	MAE	0.0777
	R²	0.90559
RF	RMSE	0.04838
	MAE	0.0328
	R²	0.985
线性回归	RMSE	0.113
	MAE	0.0821
	R²	0.9188
SVM	RMSE	0.0758
	MAE	0.0678
	R²	0.8508

从表1可以看出，CNN‐LSTM模型的预测效果最好，其次是RF模型，最差的是SVM模型。与LSTM模型相比，CNN‐LSTM模型的均方根误差平均降幅为11.9%。

从图6可以看出，这五个模型大致能够描述短期波高变化趋势。当波高快速上升时，LSTM网络的预测效果较差。而CNN‐LSTM模型的预测曲线最接近真实值，无论波高突变还是缓慢变化，该模型均能保持较高的预测能力。

此外，我们还可以通过图8确认CNN‐LSTM的性能，图8为时间序列图，展示了CNN‐LSTM在代表四个季节的不同时段内每小时观测值与预测值的对比情况。

V. 结论

本文针对提高波浪高度预测精度的实际需求，提出了一种基于卷积神经网络和长短期记忆网络的波浪高度预测模型。该模型利用卷积核与池化层的堆叠效应，提取波高相关数据的特征，并将其输入至LSTM网络以获得波高预测结果。可以得出结论：卷积操作以及池化层的非线性下采样能够有效挖掘波高相关数据中包含的特征，并减少输入神经网络的冗余信息。实验结果表明，在波高快速上升或平缓变化的情况下，CNN‐LSTM模型相比其他四种模型确实具有更好的预测效果。