【网络流】POJ3281 Dining

最新推荐文章于 2020-07-11 23:19:46 发布

原创最新推荐文章于 2020-07-11 23:19:46 发布 · 152 阅读

0 ·

CC 4.0 BY-SA版权

本文介绍了一种使用最大流算法解决N头牛与F个食物、D个饮料之间的匹配问题的方法。通过构建二分图，将牛、食物和饮料之间的喜好关系转化为边，并利用最大流算法求解最多可以满足多少头牛的食物和饮料需求。

题目大意：有 N 头牛，F 个食物，D 个饮料。N 头牛中每头牛只喜欢几个食物和饮料。每个食物和饮料只能给一头牛。而且一头牛必须同时获得一个食物和一个饮料才能满足。问至多有多少头牛可以获得满足。

我们可以大致理一下对应关系：一头牛对应几个食物，一头牛对应几个饮料，而食物和饮料是没有对应关系的。

那么可以通过牛向食物和饮料连边来体现对应关系。但是一个牛只能有一个食物和一个饮料，可以把牛拆点，连一条容量为1的边，保证一头牛不会选多个食物或饮料。最后再跑一个最大流就行了。建图大致如下：

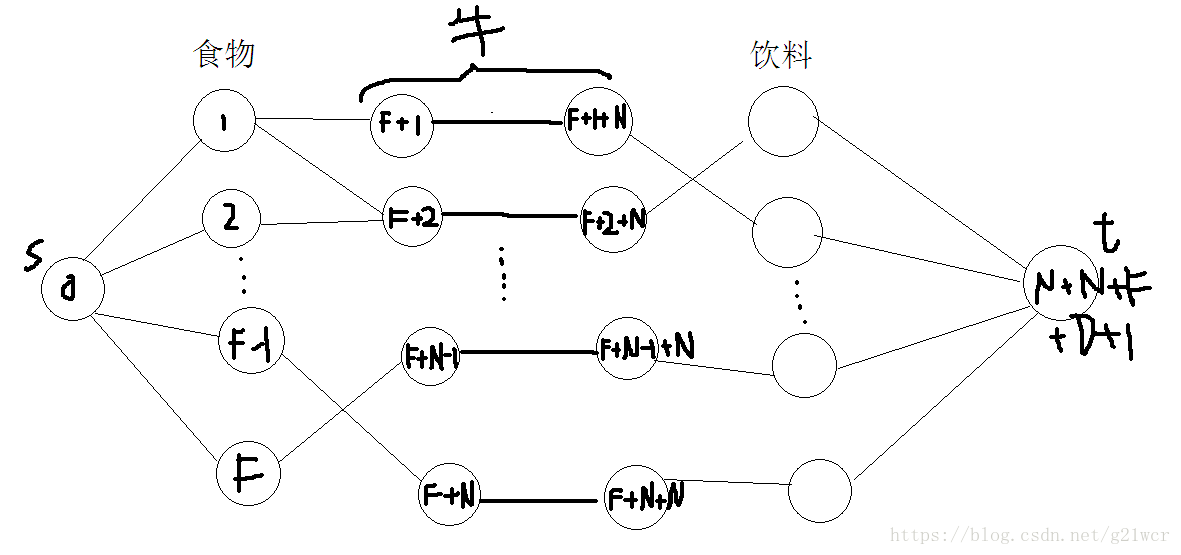
【圈里是点的编号。。饮料的我懒得画了，刷子写不下。食物和牛的连边与饮料和牛的连边我瞎画的】

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<queue>
using namespace std;
const int oo=1e7;
const int maxn=1e6;
const int maxm=1e6;
int cnt=-1,s,t;

int Head[maxn];
int Next[maxm];
int V[maxm];
int W[maxm];
int depth[maxn];

void Add(int u,int v,int w)
{
	++cnt;
	Next[cnt]=Head[u];
	V[cnt]=v;
	W[cnt]=w;
	Head[u]=cnt;
}

void addedge(int u,int v,int w)
{
	Add(u,v,w);
	Add(v,u,0);
}

int bfs()
{
	memset(depth,0,sizeof(depth));
	queue<int> Q;
	depth[s]=1;
	Q.push(s);
	while(!Q.empty())
	{
		int u=Q.front();
		Q.pop();
		for(int i=Head[u];i!=-1;i=Next[i])
		{
			if(W[i]>0&&depth[V[i]]==0)
			{
				depth[V[i]]=depth[u]+1;
				Q.push(V[i]);
			}
		}
	}
	return depth[t];
}

int dfs(int u,int dist)
{
	if(u==t)
		return dist;
	for(int i=Head[u];i!=-1;i=Next[i])
	{
		if((depth[V[i]]==depth[u]+1)&&W[i]!=0)
		{
			int di=dfs(V[i],min(dist,W[i]));
			if(di>0)
			{
				W[i]-=di;
				W[i^1]+=di;
				return di;
			}
		}
	}
	return 0;
}

int dinic()
{
	int ans=0;
	while(bfs())
	{
		while(int D=dfs(s,oo))
			ans+=D;
	}
	return ans;
}

int main()
{
	memset(Head,-1,sizeof(Head));
	memset(Next,-1,sizeof(Next));
	int N,F,D;
	scanf("%d%d%d",&N,&F,&D);
	s=0,t=N+N+F+D+1;
	for(int i=1;i<=F;++i)
	addedge(s,i,1);
	for(int i=1;i<=N;++i)
	{
		int Fi,Di,f,d;
		scanf("%d%d",&Fi,&Di);
		for(int j=1;j<=Fi;++j)
		{
			scanf("%d",&f);
			addedge(f,i+F,1);
		}
		addedge(i+F,i+N+F,1);
		for(int j=1;j<=Di;++j)
		{
			scanf("%d",&d);
			addedge(i+N+F,d+F+N+N,1);
		}
	}
	for(int i=1;i<=D;++i)
	addedge(i+F+N+N,t,1);
	printf("%d",dinic());
}