【网络流】POJ1149 PIGS

题目大意：有 m 个猪圈，每个猪圈里初始时有若干头猪。一开始所有猪圈都是关闭的。依次来了 n 个顾客，每个顾客分别会打开指定的几个猪圈，从中买若干头猪。每个顾客分别都有他能够买的数量的上限。每个顾客走后，他打开的那些猪圈中的猪，都可以被任意地调换到其它开着的猪圈里，然后所有猪圈重新关上。问总共最多能卖出多少头猪。

建图是个难点。我们考虑当一个顾客打开若干个猪圈时，这些猪圈可以看做是被合并为了一个点，因为它们之间可以相互调换。而当后面的人再次选到被开过的猪圈时，就相当于他选了与这个猪圈一起被选的猪圈。举个离子吧：

比如第一个人来，选了①号和②号猪圈。第二个人来，选了第②号猪圈和第③号猪圈。

由于第一个人选了①号和②号，那么①号和②号是可以相互调换的，第二个人选②号的时候就相当于同时选了①号和②号。

【因为可以把①号的猪转到②号，第二个人就能同时取到这两个地方的猪】

第二个人的③号没有被选过，那么他选的③号就只是③号。

下面是一个建图的例子：

【后面是选的猪圈的序号】

第一个人：①②；第二个人：②③；

第三个人：④⑤；第四个人：②⑤；

首先从源点向每个猪圈连一条边，容量为猪的数量。

【我们可以把每一个顾客看做是一个合并后的点，因为每来一个顾客，我们就可以把他所开过的猪圈合并。】

当第一个顾客来时，①和②向第一个人连一条边【把①和②合并】容量∞，然后第一个人向汇点连一条边，容量为这个人最多能买多少猪。

第二个人来时，他的②相当于①和②，那么从第一个顾客连一条边过来就相当于是合并了。

第三个人来时，④和⑤都没有被合并过，直接连过来就行了。

第四个人来时，②跟①合并过，又和③合并过，那么②代表的就是①②③这三个猪圈，我们选它最晚的合并的点就行了。

【第一个人合并了②，第二个人也合并了②，那么选第二个人来合并，因为第二个人合并了更多的点】

这样，图就建好了，如下：

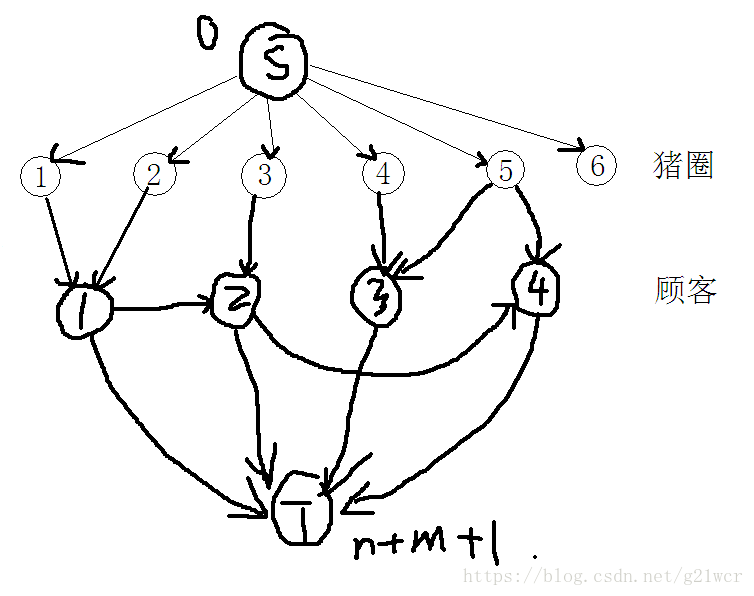
下面是代码：

#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;
const int oo=1<<30;
const int maxn=10010;
int cnt=1,Head[maxn],Next[maxn<<1],W[maxn<<1],V[maxn<<1],depth[maxn];
int last[maxn],n,m,lim,num,k,s,t;
void Add(int u,int v,int w){
	++cnt;
	Next[cnt]=Head[u];
	V[cnt]=v;
	W[cnt]=w;
	Head[u]=cnt;
}
void addedge(int u,int v,int w){Add(u,v,w),Add(v,u,0);}
int bfs(){
	memset(depth,0,sizeof(depth));
	queue<int> Q;
	depth[s]=1;
	Q.push(s);
	while(!Q.empty()){
		int u=Q.front();
		Q.pop();
		for(int i=Head[u];i;i=Next[i]){
			if(W[i]>0&&depth[V[i]]==0){
				depth[V[i]]=depth[u]+1;
				Q.push(V[i]);
			}
		}
	}
	return depth[t];
}
int dfs(int u,int dist){
	if(u==t) return dist;
	for(int i=Head[u];i;i=Next[i]){
		if(depth[V[i]]==depth[u]+1&&W[i]){
			int di=dfs(V[i],min(W[i],dist));
			if(di>0){
				W[i]-=di;
				W[i^1]+=di;
				return di;
			}
		}
	}
	return 0;
}
int dinic(){
	int ans=0;
	while(bfs()){
		while(int D=dfs(s,oo))
			ans+=D;
	}
	return ans;
}
void read(int &x){x=0;char ch=getchar();while(ch>'9'||ch<'0') ch=getchar();while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();}
int main(){
	read(m),read(n),s=0,t=m+n+1;
	for(int i=1;i<=m;++i){
		read(k);
		addedge(s,i,k);
		last[i]=i;
	}
	for(int i=1;i<=n;++i){
		read(num);
		for(int j=1;j<=num;++j){
			read(k);
			if(last[k]!=i+m)
			addedge(last[k],i+m,oo);
			last[k]=i+m;
		}
		read(lim);
		addedge(i+m,t,lim);
	}
	printf("%d\n",dinic());
}

#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;const int oo=1<<30;const int maxn=10010;int cnt=1,Head[maxn],Next[maxn<<1],W[maxn<<1],V[maxn<<1],depth[maxn],last[maxn],n,m,lim,num,k,s,t;void Add(int u,int v,int w){++cnt;Next[cnt]=Head[u];V[cnt]=v;W[cnt]=w;Head[u]=cnt;}void addedge(int u,int v,int w){Add(u,v,w),Add(v,u,0);}int bfs(){memset(depth,0,sizeof(depth));queue<int> Q;depth[s]=1;Q.push(s);while(!Q.empty()){int u=Q.front();Q.pop();for(int i=Head[u];i;i=Next[i]){if(W[i]>0&&depth[V[i]]==0){depth[V[i]]=depth[u]+1;Q.push(V[i]);}}}return depth[t];}int dfs(int u,int dist){if(u==t) return dist;for(int i=Head[u];i;i=Next[i]){if(depth[V[i]]==depth[u]+1&&W[i]){int di=dfs(V[i],min(W[i],dist));if(di>0){W[i]-=di;W[i^1]+=di;return di;}}}return 0;}int dinic(){int ans=0;while(bfs()){while(int D=dfs(s,oo))ans+=D;}return ans;}void read(int &x){x=0;char ch=getchar();while(ch>'9'||ch<'0') ch=getchar();while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();}int main(){read(m),read(n),s=0,t=m+n+1;for(int i=1;i<=m;++i){read(k);addedge(s,i,k);last[i]=i;}for(int i=1;i<=n;++i){read(num);for(int j=1;j<=num;++j){read(k);if(last[k]!=i+m)addedge(last[k],i+m,oo);last[k]=i+m;}read(lim);addedge(i+m,t,lim);}printf("%d\n",dinic());}