寻找凸包.

预备知识：叉积

u = (u1, u2)

v=(v1,v2)

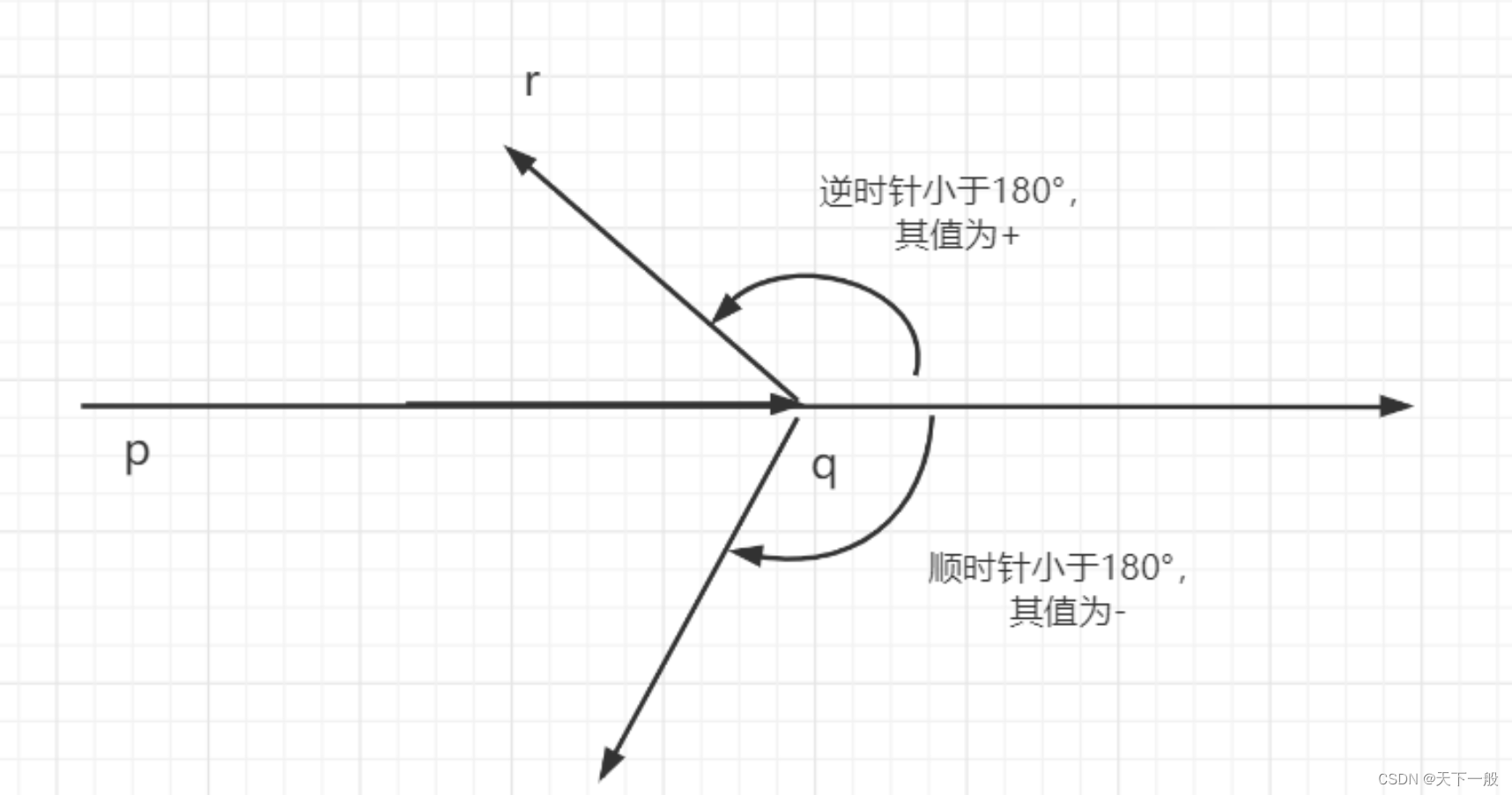
t = u*v =(u1 * v2 - u2 * v1)得到的是平行四边形的面积或者相反数。

如果t > 0的得v在u的顺时针方向上(右边)，如果t > 0得到v在u的逆时针方向(左边)。

Andrew’s Monotone chain算法

1. 按照横坐标进行降序排序。之后按横坐标排序。
2. 最左边的入栈，但不记录vis。
3. 从左到右扫描，如果栈中不足两个数，直接入栈，否则看cross(st[-2], st[-1], p)是否小于0
   • 如果大于0，直接入栈，vis[p] = true;
   • 否则栈顶出栈， vis[top] = false;
4. 到头之后，从右到左扫描，找不在栈中的vis[i] == false , 如果栈中不足m + 1个数字，直接入栈，否则看…
   • 如果大于0，直接入栈
   • 否则栈顶出栈。
5. 栈顶需要出栈，因为两个0结点。

class Solution {
    
    /*pq * qr*/
    private boolean cross(int[] p, int[]q ,int[] r) {
       	return ((p[0] - q[0]) * (r[1] - q[1]) - (p[1] - q[1]) * (r[0] - q[0])) < 0;
    }
    
    
    
    public int[][] outerTrees(int[][] trees) {
        int n = trees.length;
        if (n < 4) {
            return trees;
        }
        /* 按照 x 大小进行排序，如果 x 相同，则按照 y 的大小进行排序 */
        Arrays.sort(trees, (a, b) -> {
            if (a[0] == b[0]) {
                return a[1] - b[1];
            }
            return a[0] - b[0];
        });
        List<Integer> hull = new ArrayList<Integer>();
        boolean[] used = new boolean[n];
        /* hull[0] 需要入栈两次，不进行标记 */
        hull.add(0);
        /* 求出凸包的下半部分 */
        for (int i = 1; i < n; i++) {
            while (hull.size() > 1 && cross(trees[hull.get(hull.size() - 2)], trees[hull.get(hull.size() - 1)], trees[i]) < 0) {
                used[hull.get(hull.size() - 1)] = false;
                hull.remove(hull.size() - 1);
            }
            used[i] = true;
            hull.add(i);
        }
        int m = hull.size();
        /* 求出凸包的上半部分 */
        for (int i = n - 2; i >= 0; i--) {
            if (!used[i]) {
                while (hull.size() > m && cross(trees[hull.get(hull.size() - 2)], trees[hull.get(hull.size() - 1)], trees[i]) < 0) {
                    used[hull.get(hull.size() - 1)] = false;
                    hull.remove(hull.size() - 1);
                }
                used[i] = true;
                hull.add(i);
            }
        }
        /* hull[0] 同时参与凸包的上半部分检测，因此需去掉重复的 hull[0] */
        hull.remove(hull.size() - 1);
        int size = hull.size();
        int[][] res = new int[size][2];
        for (int i = 0; i < size; i++) {
            res[i] = trees[hull.get(i)];
        }
        return res;
    }
    
  

    public int cross(int[] p, int[] q, int[] r) {
        return (q[0] - p[0]) * (r[1] - q[1]) - (q[1] - p[1]) * (r[0] - q[0]);
    }
}

总结

• 栈可以使用数组进行优化。

• 分别寻找下凸包和上凸包。沿着排好序的点，一定是逆时针(左拐)前进。那么cross(st[-2], st[-1], p) > 0的。

• 另外进行判断的时候，寻找下凸包的时候，栈中元素是两个的时候直接入栈。

• 寻找上凸包的时候，栈中元素是m的的时候就应该直接入栈了。最少有m + 1个，m个包括最右端点 + 1就是有两个了。

• vis数组的意义是防止下凸包中的点在放入栈中，其实就是维护了当前的在凸包上的点。

• 调试技巧，直接看结果，和答案排序后进行对比，看哪个除了问题。
• 之后就可以定位到是求上凸包，还是下凸包出现了问题。
• 还可以定位到是否是统计答案的时候出现了直接使用i而不是st[i]的情况

常见错误

• 小于4个点的时候，所有的点都是凸包。如果不判断，有一个点的时候是错误的。
• 排序不对,第二维必须排序，因为是从下到上。寻找下凸包。
• vis数组忘记了
• 判断的时候，cross中的p,q,r传递的不对

题目

1. leetcode 安装栅栏 直接就是寻找的凸包的模板