ADVENT: Adversarial Entropy Minimization for Domain Adaptationin Semantic Segmentation

概览

背景

域适应在语义分割中的应用。

问题

训练集的分布与测试集的分布之间存在差异，导致在测试集上准确率不高。

动机

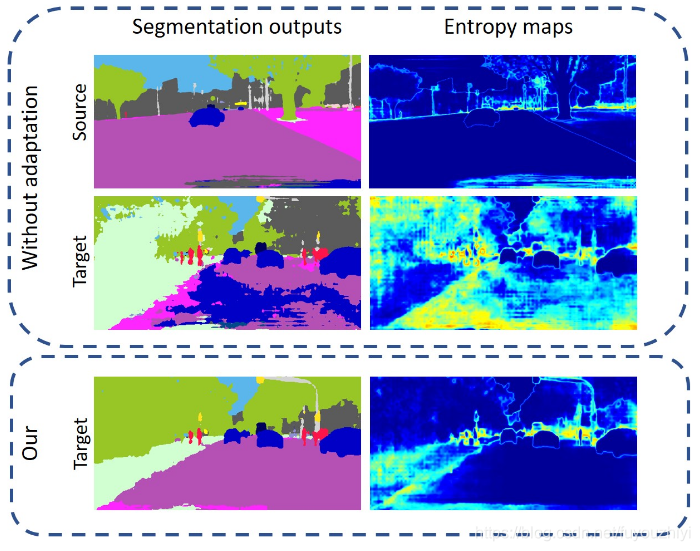
作者观察到：源域上的监督学习训练出来的模型，在与源域相似的图片上预测出来的语义分割图是低熵。而在目标域上的预测图则是高熵。如下图所示。左边是语义分割图，右边计算整个图熵值结果的可视化。
源域中的预测熵图(prediction entropy maps)像是边缘检测：在边缘部分有很高的响应值。
而在目标域，预测熵图并不是这么明显。语义分割图中有很多噪声，会造成额外的熵增。
由此，作者推测出减小目标域的熵值可以缩减源域和目标域之间的差别

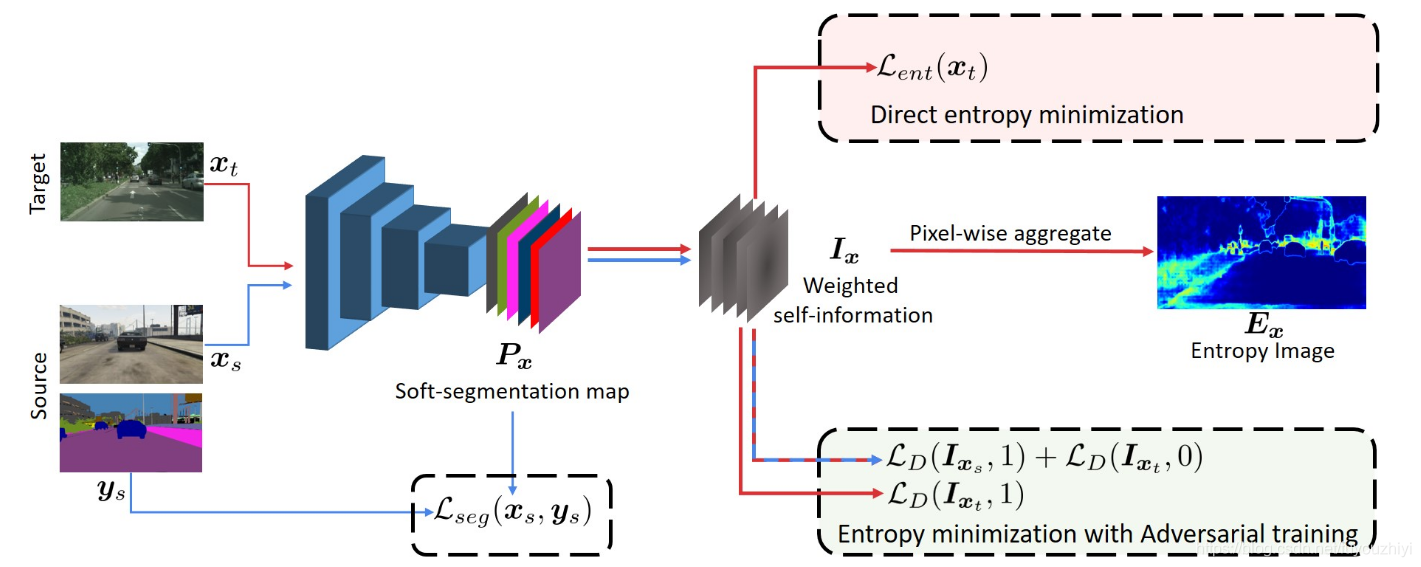
方法

１．　直接通过熵loss减小熵值
２．　通过对抗loss间接减小熵值

方法

记号

1. 源域由图像${\mathcal{X}}_S\subset {\mathbb{R}}^{H\times W\times 3}$，和　$C$类的语义分割图${\mathcal{Y}}_s\subset (1,C{)}^{H\times W}$组成.　每个像素$(h,w)$的one-hot标签表示为$y_s^{(h,w)}=[y_s^{(h,w,c)}{]}_c$
2. 语义分割网络用$F$表示，输出一个$c$通道的soft-segmentation map $F(x)={\mathbf{P}}_x=[{\mathbf{P}}_x^{(h,w,c)}{]}_{h,w,c}$
3. 目标域图片的熵图${\mathbf{E}}_{x_t}\in [0,1{]}^{H\times W}$
4. 只用源域，没有域适应时，用交叉熵作为loss函数
   $$\underset{{\theta }_F}{\min }\frac{1}{|{\mathcal{X}}_S|}\sum _{x_S\in {\mathcal{X}}_S}{\mathcal{L}}_{seg}(x_S,y_S)$$

直接熵最小化方法

香农熵的定义为
H ( X ) = − ∑ i = 1 n P ( x i ) log ⁡ P ( x i )        ,        X = { x 1 , x 2 , ⋯   , x n } H(X)=-\sum_{i=1}^n P(x_i) \log P(x_i) \; \; \;,\;\;\; X=\{ x_1,x_2,\cdots ,x_n \} H(X)=−i=1∑n​P(xi​)logP(xi​),X={x1​,x2​,⋯,xn​}
所以目标域图片的熵图${\mathbf{E}}_{x_t}$中每个点的计算方法如下：
$${\mathbf{E}}_{x_t}^{(h,w)}=\frac{-1}{\log (C)}\sum _{c=1}^C{\mathbf{P}}_{x_t}^{(h,w,c)}\log {\mathbf{P}}_{x_t}^{(h,w,c)}$$
所以熵损失函数可以定义为
$${\mathcal{L}}_{ent}(x_t)=\sum _{h,w}{\mathbf{E}}_{x_t}^{(h,w)}$$
由上面的定义我们可以看到，熵损失函数是计算feature map每一个像素的one-hot向量的香浓熵。而最后一个feature map中每一个像素都对应到原始图像中一小块区域（感受野）。

处于边缘区域的像素对应的感受野至少包含两种物体，所以导致该像素点的概率分布比较平滑。平滑的概率分布对应高的熵值。非边缘区域的像素对应的感受野一般只包含一种物体，所以提取出的特征具有判别性，它的概率分布属于尖锐的，所以熵值较低。

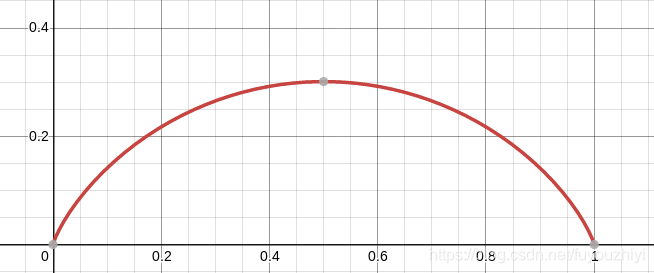
下面我们简单的香浓熵的函数图
$$H(x,y)=-x\log (x)-y\log (y),y=1-x$$
这里表示二分类问题。假设图像上有两个物体，经过语义分割网络，最终得到一个２通道的语义分割图。对于像素$(h,w)$的预测出的onehot向量，我们用向量$(x,y)$表示。下图可以看到，当$x,y$其中一个趋近于１时，即能肯定的判断出该像素属于哪个类别时，熵loss很小。反之，当$x,y$差别不大，即不好判断像素属于哪个类别时熵loss很大
在线绘图工具

由此可见，熵loss的存在为了让预测出的onehot向量的分布更加尖锐。

论文采用自训练(self-training , ST)

对抗学习最小化熵

前面直接最小化熵损失函数，忽略了语义的结构关系。在语义分割无监督域适应中，结构化的输出空间是有益的。

所以论文引入对抗学习框架间接减少熵。通过拉近源域和目标域熵的分布，缩小源域与目标域之间的分布差异。主要方法：weighted self-information space

动机：我们训练的模型只有在预测与源域相似的图像上才能得到低熵的预测图。所以通过对其源域和目标与的weighted self-information分布，间接地减小目标域的熵

图片$x$中的点$(h,w)$是第$c$类的概率表示为：${\mathbf{P}}_x^{(h,w,c)}$.
定义该点的self-information为：$-\log {\mathbf{P}}_x^{(h,w,c)}$.　则熵${\mathbf{E}}_x^{(h,w)}$是self-information的期望：${\mathbb{E}}_C[-{\mathbf{P}}_x^{(h,w,c)}]$
定义self-information map ${\mathbf{I}}_x^{(h,w)}$为：${\mathbf{I}}_x^{(h,w)}=-{\mathbf{P}}_x^{(h,w)}\cdot \log {\mathbf{P}}_x^{(h,w)}$

论文的目的：让目标域的${\mathbf{I}}_x^{(h,w)}$与源域的尽可能相像。而源域的${\mathbf{I}}_x^{(h,w)}$意味着熵很小，如果目标域的${\mathbf{I}}_x^{(h,w)}$和源域的类似，此时目标域的熵就降下来了。所以论文需要构建一个判别器，来判断　${\mathbf{I}}_x^{(h,w)}$属于哪个域
判别器的输入是源域和目标域的　${\mathbf{I}}_x^{(h,w)}$　，定义源域的标签为１，目标域的标签为０，输出域标签的预测。

判别器D的loss为
$$\underset{{\theta }_D}{\min }\frac{1}{|{\mathcal{X}}_s|}\sum _{x_s}{\mathcal{L}}_D({\mathbf{I}}_{x_s},1)+\frac{1}{|{\mathcal{X}}_t|}\sum _{x_t}{\mathcal{L}}_D({\mathbf{I}}_{x_t},0)$$

语义分割网络Ｆ的loss为
$$\underset{{\theta }_F}{\min }\frac{1}{|{\mathcal{X}}_s|}\sum _{x_s}{\mathcal{L}}_{seg}(x_s,y_s)+\frac{{\lambda }_{adv}}{|{\mathcal{X}}_t|}{\mathcal{L}}_D({\mathbf{I}}_{x_t},1)$$