频谱周期性复制

冈萨雷斯《数字图像处理》中关于傅里叶变换与取样理论

在信号处理中，冲激取样（也称为理想取样）是指用一系列等间隔的冲激函数对连续时间信号进行采样的过程。这一过程在时域表现为原始信号与冲激串函数的乘积，在频域则导致信号频谱的周期性扩展。以下从数学角度解释这一现象的原理。

冲激取样的时域表示

设原始连续信号为 $f(t)$，取样周期为 $\Delta T$，则取样后的信号 $\tilde{f}(t)$ 可表示为：

$$\tilde{f}(t)=f(t)\cdot \sum _{n=-\infty }^{\infty }\delta (t-n\Delta T)$$

其中，$\delta (t)$ 为单位冲激函数。该表达式表示将原始信号 $f(t)$ 与一个周期为 $\Delta T$ 的冲激串相乘，从而在时间轴上以 $\Delta T$ 为间隔取样。

傅里叶变换下的频域表示

根据傅里叶变换的乘积定理，时域乘积对应于频域卷积。因此，取样后的信号 $\tilde{f}(t)$ 的傅里叶变换 $\tilde{F}(\mu )$ 为：

$$\tilde{F}(\mu )=\mathcal{F}[\tilde{f}(t)]=\mathcal{F}[f(t)]\ast \mathcal{F}\left[\sum _{n=-\infty }^{\infty }\delta (t-n\Delta T)\right]$$

冲激串的傅里叶变换是一个周期性的频域序列，其周期为 $\frac{1}{\Delta T}$，即取样率。具体地，该冲激串的傅里叶变换为：

$$\mathcal{F}\left[\sum _{n=-\infty }^{\infty }\delta (t-n\Delta T)\right]=\frac{1}{\Delta T}\sum _{k=-\infty }^{\infty }\delta \left(\mu -\frac{k}{\Delta T}\right)$$

将其代入上式，可得：

$$\tilde{F}(\mu )=F(\mu )\ast \left(\frac{1}{\Delta T}\sum _{k=-\infty }^{\infty }\delta \left(\mu -\frac{k}{\Delta T}\right)\right)$$

根据卷积的性质，$F(\mu )$ 与一系列冲激函数的卷积，相当于将 $F(\mu )$ 以 $\frac{1}{\Delta T}$ 为周期进行复制并叠加，形成周期性的频谱结构。因此，取样后的频谱 $\tilde{F}(\mu )$ 是原始频谱 $F(\mu )$ 的无限周期扩展，周期为 $\frac{1}{\Delta T}$ 。

频谱周期性的数学解释

由于冲激串的傅里叶变换本身是周期性的，因此其与原始信号频谱的卷积自然导致取样信号频谱的周期性。这种周期性复制现象称为“频谱混叠”（spectral aliasing），当原始信号的带宽超过 $\frac{1}{2\Delta T}$ 时，相邻周期的频谱会发生重叠，造成信息丢失。

示例代码

代码展示了原始信号和取样信号的频谱，取样信号的频谱呈现出明显的周期性结构。

---

import numpy as np
import matplotlib.pyplot as plt
 
plt.rcParams['font.family'] = 'SimHei'  # 黑体，适用于中文
plt.rcParams['axes.unicode_minus'] = False  # 正确显示负号

# 原始连续信号（高斯函数）
t = np.linspace(-10, 10, 2000)
f = np.exp(-t**2)

# 冲激取样：每隔一定间隔保留一个点，其余为0
sampling_interval = 10
sampled_f = np.zeros_like(f)
sampled_f[::sampling_interval] = f[::sampling_interval]

# 傅里叶变换
F_original = np.fft.fftshift(np.abs(np.fft.fft(f)))
F_sampled = np.fft.fftshift(np.abs(np.fft.fft(sampled_f)))

# 频率轴
freq = np.fft.fftshift(np.fft.fftfreq(len(t), d=(t[1] - t[0])))

# 可视化：统一使用 2x2 布局
fig, axs = plt.subplots(2, 2, figsize=(12, 8))


axs[0, 0].plot(t, f)
axs[0, 0].set_title("原始连续信号")
axs[0, 0].set_xlabel("时间 (s)")
axs[0, 0].set_ylabel("振幅")
axs[0, 0].grid(True)

axs[0, 1].plot(freq, F_original)
axs[0, 1].set_title("原始信号频谱")
axs[0, 1].set_xlabel("频率")
axs[0, 1].grid(True)

axs[1, 0].plot(t, sampled_f)
axs[1, 0].set_title("冲激取样后信号")
axs[1, 0].set_xlabel("时间 (s)")
axs[1, 0].set_ylabel("振幅")
axs[1, 0].grid(True)

axs[1, 1].plot(freq, F_sampled)
axs[1, 1].set_title("冲激取样后频谱（周期性副本）")
axs[1, 1].set_xlabel("频率")
axs[1, 1].grid(True)

plt.tight_layout()
plt.show()

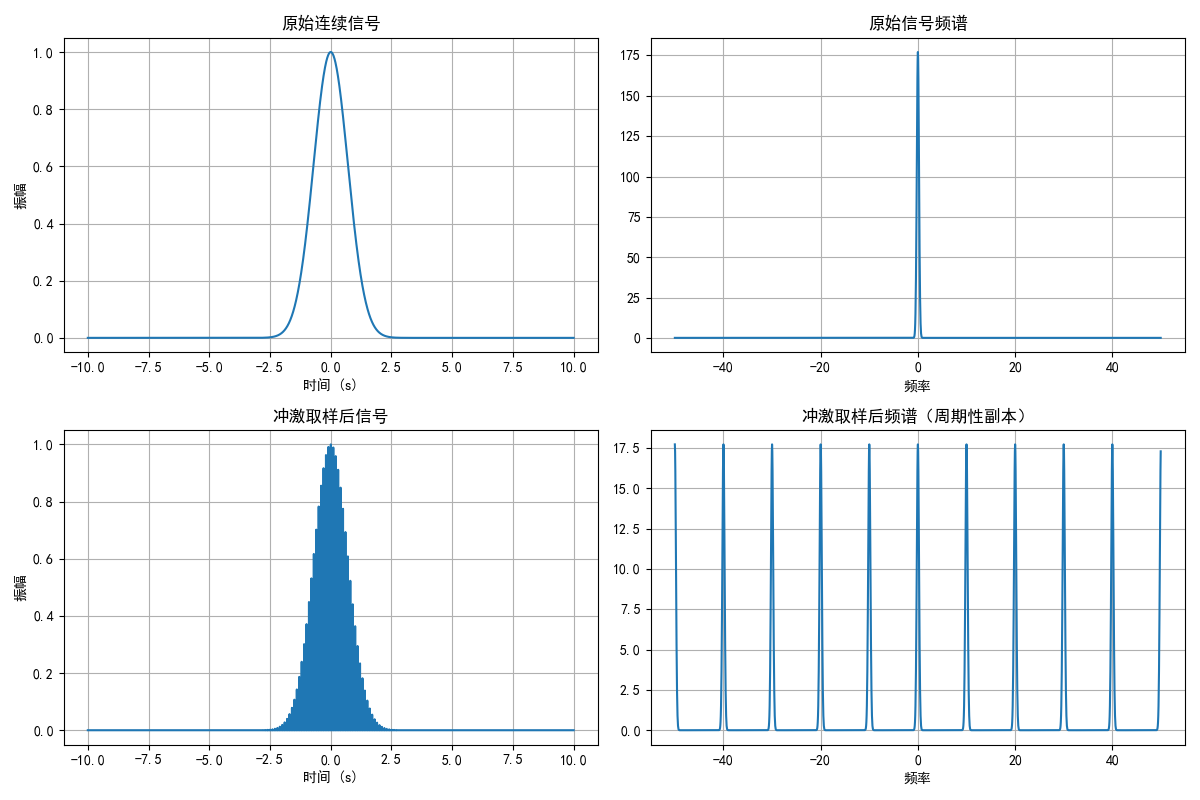
取样周期
$$T=\frac{10-(-10)}{2000}\ast samplinginterval=\frac{1}{10}$$

sampling_interval = 2

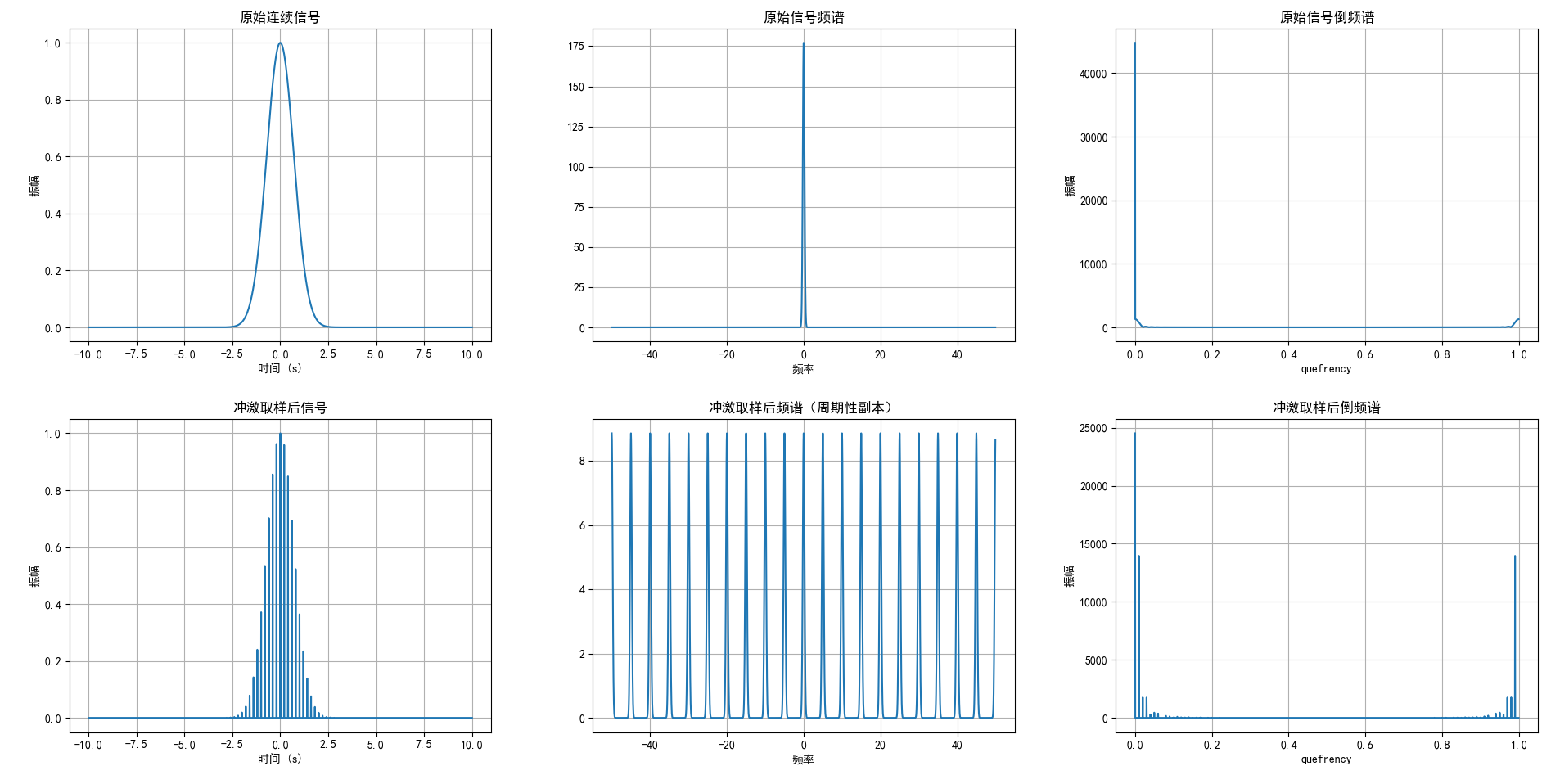
倒频谱

倒频谱中出现明显峰值，说明频谱中存在周期性复制，其根本原因来自于采样过程在频域中的数学特性。我们来深入解释这个现象。

---

🧠 原理解析：采样导致频谱周期性复制

根据冲激采样理论：

• 在时域中，采样是将连续信号与冲激串相乘。
• 在频域中，这对应于原始频谱与冲激串频谱的卷积。
• 冲激串的频谱是一个周期性的冲激序列，其周期为采样率 $$f_s$$。
• 卷积结果就是将原始频谱以 $$f_s$$ 为间隔进行无限复制。

这就是频谱周期性复制的来源。

---

🔍 倒频谱为何能检测频谱周期性？

倒频谱的定义是：

对信号频谱取对数后再进行一次傅里叶变换。

这一步的作用是将频谱中的周期性结构（如副本间距）转化为倒频谱中的单一峰值。

举例说明：

• 如果频谱中每隔 100Hz 出现一个副本（周期性复制），
• 那么倒频谱中会出现一个峰值，其位置为 $$1/100=0.01s$$，
• 这个位置就是频谱副本之间的间隔（周期）的倒数。

因此：

倒频谱中的峰值位置揭示了频谱副本之间的间距，从而判断是否存在周期性复制。

---

📌 应用场景

• 在不知道采样率的情况下，倒频谱可以帮助我们估算频谱副本间距。
• 如果副本间距太小（即采样率太低），就可能发生混叠。
• 倒频谱图中峰值靠近零 → 频谱副本密集 → 可能混叠。

---

import numpy as np
import matplotlib.pyplot as plt
 
plt.rcParams['font.family'] = 'SimHei'  # 黑体，适用于中文
plt.rcParams['axes.unicode_minus'] = False  # 正确显示负号

# 原始连续信号（高斯函数）
t = np.linspace(-10, 10, 2000)
f = np.exp(-t**2)

# 冲激取样：每隔一定间隔保留一个点，其余为0
sampling_interval = 20
sampled_f = np.zeros_like(f)
sampled_f[::sampling_interval] = f[::sampling_interval]

# 傅里叶变换
F_original = np.fft.fftshift(np.abs(np.fft.fft(f)))
F_sampled = np.fft.fftshift(np.abs(np.fft.fft(sampled_f)))

# F_original = np.fft.fft(f)
# F_sampled = np.fft.fft(sampled_f)

# 频率轴
freq = np.fft.fftshift(np.fft.fftfreq(len(t), d=(t[1] - t[0])))

# 倒频谱
# 计算倒频谱
F_original_log = np.log(F_original + 1e-10)  # 避免对零取对数
F_sampled_log = np.log(F_sampled + 1e-10)
cepstrum_original = np.fft.fft(F_original_log)
cepstrum_sampled = np.fft.fft(F_sampled_log)
cepstrum_magnitude_original = np.abs(cepstrum_original)
cepstrum_magnitude_sampled = np.abs(cepstrum_sampled)

cepstrum_quefrency = np.arange(len(cepstrum_magnitude_original)) / len(t)
cepstrum_quefrency_sampled = np.arange(len(cepstrum_magnitude_sampled)) / len(t)


# 可视化：统一使用 2x2 布局
fig, axs = plt.subplots(2, 3, figsize=(12, 8))


axs[0, 0].plot(t, f)
axs[0, 0].set_title("原始连续信号")
axs[0, 0].set_xlabel("时间 (s)")
axs[0, 0].set_ylabel("振幅")
axs[0, 0].grid(True)

axs[0, 1].plot(freq, F_original)
axs[0, 1].set_title("原始信号频谱")
axs[0, 1].set_xlabel("频率")
axs[0, 1].grid(True)

axs[0, 2].plot(cepstrum_quefrency, cepstrum_magnitude_original)
axs[0, 2].set_title("原始信号倒频谱")   
axs[0, 2].set_xlabel("quefrency")
axs[0, 2].set_ylabel("振幅")
axs[0, 2].grid(True)

axs[1, 0].plot(t, sampled_f)
axs[1, 0].set_title("冲激取样后信号")
axs[1, 0].set_xlabel("时间 (s)")
axs[1, 0].set_ylabel("振幅")
axs[1, 0].grid(True)

axs[1, 1].plot(freq, F_sampled)
axs[1, 1].set_title("冲激取样后频谱（周期性副本）")
axs[1, 1].set_xlabel("频率")
axs[1, 1].grid(True)

axs[1, 2].plot(cepstrum_quefrency_sampled, cepstrum_magnitude_sampled)
axs[1, 2].set_title("冲激取样后倒频谱")
axs[1, 2].set_xlabel("quefrency")
axs[1, 2].set_ylabel("振幅")
axs[1, 2].grid(True)

plt.tight_layout()
plt.show()