Dijkstra算法求最短路径

最新推荐文章于 2025-09-13 11:56:24 发布

原创最新推荐文章于 2025-09-13 11:56:24 发布 · 1.2k 阅读

1 ·

CC 4.0 BY-SA版权

本文详细介绍了如何使用Dijkstra算法求解从顶点a到顶点h的最短路径，包括算法的设计思路、实现步骤及源码解析。通过将顶点集合分为已求最短路径集合S和未确定集合V，逐步迭代找到最短路径。

1.问题

对于下图使用Dijkstra算法求由顶点a到顶点h的最短路径，按实验报告模板编写算法。

2. 解析

设置集合，把顶点集合V分成两组S V，已求出的顶点（最短路径的顶点）的集合为S，未确定的顶点集合为v。
初始化
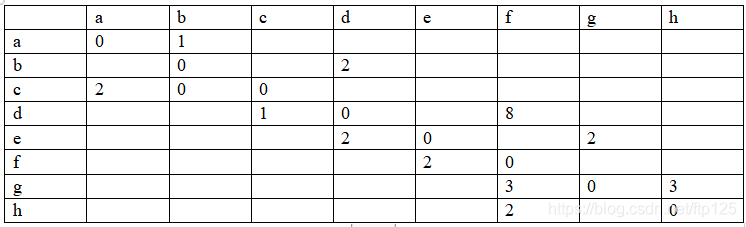
在这里插入图片描述

依次选取最短路径点的情况下：
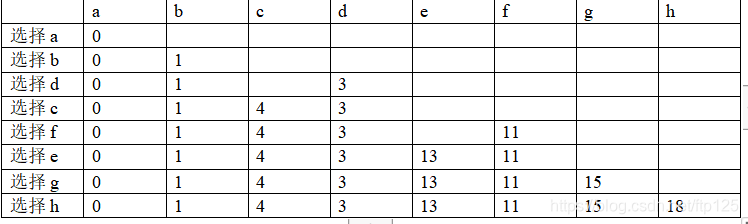
在这里插入图片描述

3.设计

//先输入边长
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
scanf("%d",&aaa[i][j] ) ;

}

for (w = 0; w < n; w++)
{
// 次求得v0到某个顶点v的最短路径就加到S中

// v为上次选入集合S中的点，以点V为中间点 d0v下一点小于 D[w] ，进行判断
if (!final[w] && (min+aaa[v][w]<D[w]))
{
D[w] = min + aaa[v][w];
p[w][w] = 1;
}
}

4. 分析

时间复杂度时O（n^2）.

5.源码

#include
#include

#define max 99
using namespace std;

int v0 = 0;
int v,w;
int aaa[8][8], D[8], p[8][8], final[8];
int n = 0;

void zuiduan()
{
for (v = 0; v < n; v++)
{
final[v] = 0; D[v] = aaa[v0][v];
for (w = 0; w < n; w++) p[v][w] = 0;
if (D[v] < max) {p[v][v0] = 1; p[v][v] = 1;}
}
D[v0] = 0; final[v0]=1;
// 次求得v0到某个顶点v的最短路径就加到S中
for (int i = 1; i < n; i++)
{
int min = max;
for (w = 0; w < n; w++)
{

           if (!final[w]) //如w顶点在
           {                 
                if (D[w] < min) {v = w; min = D[w];}
           }
      }
      final[v] = 1; //选该点加到S中
      for (w = 0; w < n; w++)//更新
      {
           /*  v为上次选入集合S中的点，以点V为中间点  d0v下一点小于 D[w] 进行判断 */               
           if (!final[w] && (min+aaa[v][w]<D[w]))
           {
                D[w] = min + aaa[v][w];                 
                p[w][w] = 1;
           }
      }
 }

}

int main()
{
scanf("%d",&n );
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
scanf("%d",&aaa[i][j] ) ;

     }
}
zuiduan();
  
printf("a到h最短距离：%d\n" ,D[n-1]);
return 0;

}