量化面试题 | 动态规划之Dynamic card game

问题描述

来自小绿书P127，动态规划那一节。假设有一副扑克牌，一共52张，26张红牌26张黑牌，现在充分洗牌，然后一张一张摸牌，可以看到摸出的牌且不放回。你可以随时停止这个游戏。停下后，你的收益是摸出的红牌数减去摸出的黑牌数。请问你该如何设计策略，以及你的期望收益是多少呢？

思路

这是一个动态规划的问题。现在假设还剩下b张黑牌和r张红牌，由对称性知道，假如在此时此刻停止，那么收益将是26-r-(26-b) = b-r
那么假如不停止呢，期望收益将是$\frac{b}{b+r}Ef(b-1,r)+\frac{r}{b+r}Ef(b,r-1)$。这里$Ef(b,r)$表示按照目前的策略，当前如果剩下b张黑牌和r张红牌，最终收益的期望值，于是就有了如下递推式：
$$Ef(b,r)=\max (b-r,\frac{b}{b+r}Ef(b-1,r)+\frac{r}{b+r}Ef(b,r-1))$$

有没有觉得这很像美式期权的过程，美式期权的二叉树定价就是这样。

最后确定边界条件。当$b=0$时，$Ef(b,r)=0$，因为已经剩下0张黑牌，即黑牌全都被摸完了，所以一定要把红牌也全都摸完才能使得亏损最小，也就是亏损是0。当$r=0$时，显然只剩黑牌了，就不会再摸了，此时$Ef(b,r)=b-r=b$。这样边界条件就确定了。说是边界条件，其实更类似于一种terminal condition终端条件。

代码

有了上面的递推式，我们就可以写一个代码。不过由于总会重复计算一些值，因此我们可以用一个哈希表记录已经算过的值，就避免了重复计算，可以很快得到结果。

ans = {}
def f(b, r):
    if b == 0:
        return 0
    if r == 0:
        return b
    if (b, r) in ans:
        return ans[(b, r)]
    # print('f(b-1, r) = {}, f(b, r-1) = {}'.format(f(b-1, r), f(b, r-1)))
    res = max(b-r, (b*f(b-1,r)+r*f(b,r-1))/(b+r))
    ans[(b, r)] = res
    return res
print(f(26, 26))

最终输出的结果是2.624475548993925。于是我们的期望收益大约是2.62，也就是可以支付2.62元来玩这个游戏。
然后其实可以把所有结果都得到，也就是得到所有的$Ef(b,r),0\le b,r\le 26$

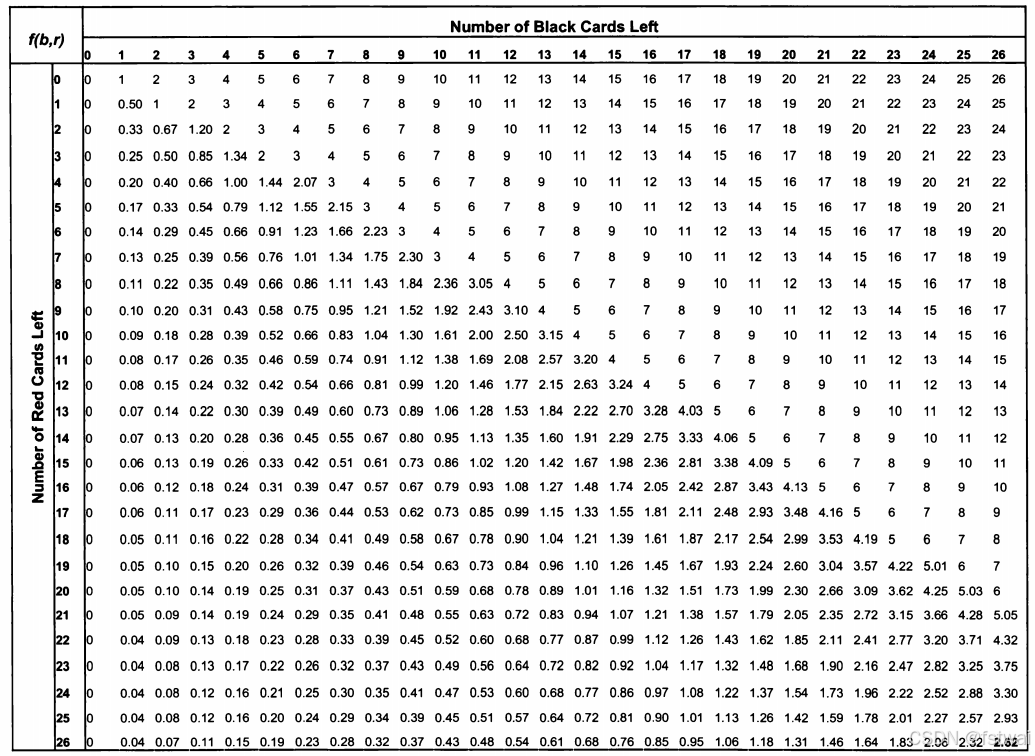
和美式期权类似，当$Ef(b,r)=b-r$时，就应该停止继续摸牌，就类似于美式期权的Stopping region了。上图有一个比较明显的整数和非整数的分界线，大概就是应该停止摸牌还是继续摸牌的分界线。当$Ef(b,r)>b-r$时，就应该继续摸牌（也就是图片中左下的部分，这一部分还剩的红牌数r很多，应该继续摸牌）。