图立顿模型：自编码离散空间

新“图立顿”模型：一种自编码为三价自旋网络的计算离散空间

4.1. 引言

在本章中，我们提出一种新型模型，特别适用于解决非欧几里得空间中的物理问题。这些空间可能融合了邻近性概念（如地理信息系统）、拓扑概念（如社交网络）、信息概念以及代数概念（如某些局部对称性的不变性）。

我们的模型旨在为数字物理提供一个框架，它在基于集合论的空间定义上实现了概念性突破。我们可以根据其度量计算引力场。在此，我们从信息论的角度明确了该模型的形式体系，从而开辟了在网络[ASC 08, ASC 09a, ASC 09b, ASC 10]中的应用。

该模型是一个多层次的复杂系统，其基本层级是三价图。
第二层级是在拓扑图结构中对信息进行编码。
第三是局部对称性和代数性质的编码。
第四是子图的集合作为晶格型网络中的超节点，呈现出度量、维度和曲率。

在这个模型的每个层级上都有可能保持良好的一致性。我们在基础层级上优化结构的简洁性，同时允许被建模系统中产生高度的复杂性。

该模型族旨在提供一个统一的框架，以建立一种新的万物理论，在理论物理中将量子物理现象、标准模型知识与引力以及根据广义相对论所理解的时空概念统一起来。我们所处理的是一个离散模型，而非连续模型。关于宇宙的本质是离散的还是连续的，目前仍存在争论。甚至有人推测现实可能是两者的结合：[CHA 10] “我们考察这样一种假设：时空是连续四维流形与有限空间的乘积”。

其他人假设，一个离散的（可能是有限的）系统足以产生表观连续性，而这种表观连续性是对离散系统的近似。本工作的主要成果是证明了一种迄今为止被视为连续过程的现象，能够在我们的离散模型中自然出现：引力。由于它源自一个简单图，我们称之为“图引力”。类似的双关语此前已被用于一种在图中研究量子物理的方法，称为“量子图性”（参见 Markopoulou et al.[MAR 04]和 Konopka et al.[KON 08]）。

然而，这些方法有所不同；物理学家已构建了多个离散模型、图或网络，以通过将现有模型保持为离散形式来实现连续的物理方程。这些方法是自上而下的，因为它们从已知结果出发，寻找一致的底层结构。

我们的方法是自下而上的，从一个简单的模型（集合论层级，数学基础）开始，根据经济性原则——“奥卡姆剃刀原理”（如无必要，勿增实体）[DE 19, DE 40]，构建一个通向复杂现实的分层模型。

4.2. 图引力，自下而上的方法

在我们的自下而上的方法中，我们从一个三价无向图开始。

4.2.1. 构造

4.2.1.1. 定义

一个graphiton模型是一个三价图，它需满足至少两个性质：大尺度上的准不变性（若忽略少量扰动，则图中大量均匀分布的节点在拓扑上是等价的）以及通过存在编码比特1的三角环来刻画小尺度下的局部几何结构。

图立顿是图立顿模型的基本元素，它只是一个节点，具有三个端点，每个端点连接到另一个图立顿。

因此，虽然任何完全三价图都是图立顿的组合，但要成为模型，它必须满足全局准不变性和局部几何编码的性质。

一种图立顿模型可以在不同尺度上进行解释。我们将区分三种尺度。

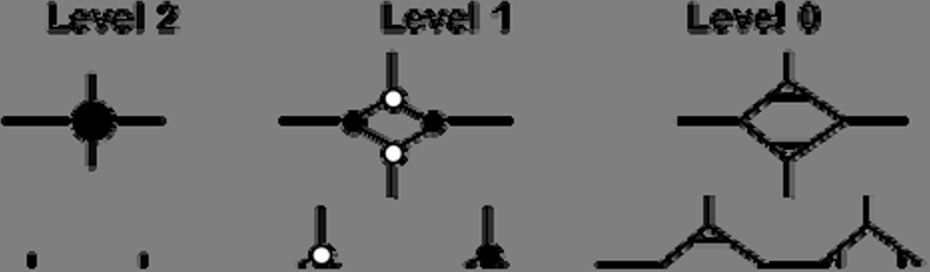一个简单节点、(b)一个子图的三层视图)

第0层是基础层级，其中模型是一个简单的无向三价图，任何节点或连接都不携带附加信息。

第1层通过向第0层的每个节点添加一个二元属性获得；每个节点携带一个比特，取值为 0 或值为 1。

第2层通过第1层信息图与第0层之间的等价性由亚历山大和布里格斯提出的 T2变换（见图4.3）[ALE 26]确保，该变换将第1层每个值为1的节点替换为由三个第0层节点组成的三角形，并且不改变第1层上值为0的节点。

如果该图在第1层是信息同质的，即包含等量的比特 0 和比特1，而其在第0层的等价形式将使其节点数量（以及连接数量）加倍。

除非另有明确说明，我们始终在信息同质图上进行工作。

我们的模型具有自然编码和规则且同质的信息，这可以被视为针对某一哈密顿量的物理上最优极化，从而定义了系统的基态。该系统可能因窄比特 0 和 1 的反转而被破坏，并包含附加信息。

我们表明，这种反转仅通过亚历山大的 T1 变换实现（见图 4.2），这些变换提供了一系列动态不变系统，并间接地实现了沃尔夫勒姆所讨论的因果不变性 [WOL02]。T1 变换直观上是三价图可能发生的最简单、最现实且最经济的演化方式。它作用于两个节点之间的连接，并涉及这两个节点各自的另外两个邻居。当该连接处于水平视图时，这六个节点构成一个 H 形的面，而 T1 变换将 H 旋转 90 度。这一过程可以通过一个瞬态在连续基础上完成，在此瞬态中，四价节点 5 位于 X 形图形的中心（即图 4.2 中节点 5 和 6 合并时的情况）。

在每个连接处，我们可以应用两种不同的变换 T1，具体取决于第一个相邻节点是与第二个相邻节点相连，还是沿另一方向连接。

如果图是局部平面的，则一种T1变换保持平面性，而另一种则不保持，从而确定将应用的隐含变换。

4.2.1.2. 扰动

在第1层（见图4.1），扰动是指由两个节点携带的两个比特的0和1值发生反转，这两个节点要么是相邻的（距离0），要么是近邻的（距离1，中间相隔一个节点）：

1 0 ↔ 0 1
1 1 0 ↔ 0 1 1，1 0 0 ↔ 0 0 1（图4.4）。

4.2.1.3. 系统作为空间的维度

图的维度取决于所选择的尺度。我们区分三个层级：

• 超局部维度 ：在一个节点周围，三价图的维度为 2 [04, AMB CAR]，并被视为六角晶格的局部限制。
• 局部尺度 ：在超级节点内部，结构为二叉树图，其维度是无限的，因为在距离r处的邻居数量以2r的速度增加，因此比任何有限维度d下的 rd增长得更快。
• 全局维度 ：由所选的规则系统决定（网格为2，超金刚石[ASC 08、ASC 09a、ASC 09b，单纯形为ASC 10], n-1等）。

4.2.2. 空间的全局拓扑

如果网络被选择为无限的，则全局拓扑是平坦的。

如果网络是闭合的，它就会变得弯曲，例如在n维环面中。

闭合可能意味着一种偏移，如果一条线在遍历后未能与自身相接，而是与邻近者相接，就像非交换环面那样。

闭合可能会反转定向，形成莫比乌斯带、克莱因瓶或其他非定向空间 [LUM 01]。

4.2.3. 晶格规则性

4.2.3.1. 规则晶格

我们可以将我们的模型应用于任何规则晶格，例如方格晶格、棋盘晶格，甚至A、D、E、F族中的晶格。

我们可以进一步研究将其应用于准规则晶格：准晶体 [SAD 97] 和彭罗斯铺砖 [CON 90]。

4.2.3.2. 几乎正则性

我们可以将可接受模型的集合扩展到几乎正则格，其定义为允许存在一定数量不规则性的规则晶格，即对于具有 nd个节点和全局维度 d 的图，其不规则性数量为 < n(d -1 )。

4.2.3.3. 局部规则性

作为几乎正则性的一个特例，我们可以构建在物理上对应于天然晶体结构的模型。这些模型在维度为 d‐1 的表面上存在不规则性，局部规则但整体各向同性。空间被分割成若干不规则晶体块，这些晶体块本身是规则的，但彼此之间并不平行。

因此，研究晶间壁的动态行为将是有用的。从数学角度来看，几乎正则性与局部规则性是相似的，因为它们相对于必要的全局规则性所引起的不规则性数量都很小。

4.2.4. 内禀空间

图灵子模型的根本优势在于其创建了内禀空间。从外部看，该系统是一个图，其节点并不在任何空间中进行坐标定位（与之前所有物理离散化方法不同）。但由于信息被编码于该图的拓扑结构之中，该模型获得了度量空间所需的特性，而不仅仅依赖于图的内部度量——后者本身是不足的。图灵子模型是一种能够模拟空间的信息系统。这种空间相当丰富，因为它是黎曼的 [PEN 05]，允许局部曲率存在，并可为里奇平坦，在无扰动的情况下，第2层的任意节点在拓扑上等价于 [ASC 08, ASC 09a, ASC 09b, ASC 10]。最重要的是，局部扰动会线性地诱导出曲率，从而在空间任意点引起测地线倾斜，形成引力场。该引力场朝向产生它的扰动源，并具有可加性；这些正是反映质量扰动效应的引力场所必需的条件。因此，这一空间非常自然地构成了广义相对论的框架。

然而，尽管空间由于规则网络标记了方向而呈现局部各向异性，所诱导出的引力场仍保持各向同性，并不局限于网络的方向。因此，系统在引力场作用下的运动可以沿任意方向进行，而不受网络方向的约束。

4.2.5. 空间作为网络

空间的终极本质是一个三价图，且该图的某些拓扑特征编码了质量效应，从而影响曲率，并可能计算出里奇曲率和爱因斯坦场方程[PEN 05]，这一总体思想由沃尔夫勒姆[WOL 02]提出。

我们对这一概念做出的根本性贡献，也是实现有效实施的关键，在于在第1层的图中有效地添加一层信息，该层与第2层的规则结构相关联。

这一层使得信息能够在图内沿每个维度的两个方向（双向）在选定距离内进行内在移动，并能够计算引力场和里奇张量[PEN 05]。在沃尔夫勒姆提出的最随机的图模型中，这些计算是不可能的，也无法明确定义里奇张量的概念。而在基于规则阵列的其他离散模型中，作者则假设了所有空间的存在，即局部欧几里得且连续外在的空间，并将他们的模型嵌入其中以获得度量和坐标。这种方法远不如沃尔夫勒姆的概念来得严谨和优雅！因此，我们继承了沃尔夫勒姆所提出的模型的极致优雅之处——这是唯一一种无需嵌入到其他空间中即可进行计算的内在系统模型。但我们通过引入规则性和局部方向的拓扑编码约束，克服了其缺乏度量的问题。

4.3. 数学形式体系

我们给出了图灵子模型的正式描述。

4.3.1. 定义

定义 4.1. – r阶二叉树：

$$
\mathcal{T} r := \left{ \text{nodes } {n_k} {k=0}^{2^r - 1}, \text{links } {(n_0, n_1)} \cup \bigcup_{k=1}^{2^{r-1}-1} {(n_k, n_{2k})} \cup \bigcup_{k=1}^{2^{r-1}-1} {(n_k, n_{2k+1})} \right}
$$

图4.5给出了 $\mathcal{T}_3$ 图及其来自 $\mathcal{T}_2$ 的子树的示例。

的子图)

定义 4.2. – descendants if $k < 2^{r-1}$:

$$
\text{descendants}(n_k, \mathcal{T} r) =
\begin{cases}
{n {2k}, n_{2k+1}} \cup \text{descendants}(n_{2k}, \mathcal{T} {r-1}) \cup \text{descendants}(n {2k+1}, \mathcal{T}_{r-1}), & \text{if } k < 2^{r-1} \
\emptyset, & \text{else}
\end{cases}
$$

定义 4.3. – subtree in $n_k$:

$$
\text{subtree}(n_k, \mathcal{T}_r) = {n_k} \cup \text{descendants}(n_k, \mathcal{T}_r)
$$

定义 4.4. – a triple-binary($\Xi$) module using a binary tree($\mathcal{T}$) to build a trivalent graph:

$$
\text{module}(r) = \Xi(\mathcal{T}_r)
$$

图4.6 显示了一个三元二进制操作符 $\Xi$ 将 t 个三价图粘合在一起，如图所示。

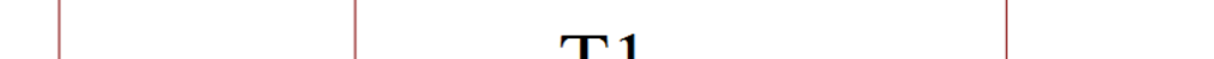显示 12 个叶节点)

定义 4.5. – 我们定义整数的二进制分解：

$$
\beta(K) := {b_{i,K}} \in {0,1}^{\lfloor 1 + \log_2 K \rfloor} \quad \text{such that} \quad K = \sum_{i=0}^{\lfloor \log_2 K \rfloor} b_{i,K} 2^i
$$

定义 4.6. – 我们定义一个四元数的频率：

$$
\omega(x) := \frac{1}{\pi} \arccos(\text{Re}(x))
$$

定义 4.7. – 我们根据四元数的频率定义其对数：

$$
\log(x) = \log(|x|) + \pi \omega(x) \frac{\text{Im}(x)}{|\text{Im}(x)|}
$$

定义 4.8. – 我们定义一个由 r 对频率和虚方向组成的族：

$$
\Omega_r := \left{ {\omega_k, u_k} \mid k \in \mathbb{N} \cap [0,r[, \omega_k \in ]0,1], u_k = \text{Im}(u_k), |u_k|=1 \right}
$$

定义 4.9. – 我们定义一个递增积的序列：

$$
\forall K \in \mathbb{N} \cap [0,2^r[, \quad \zeta(K, \Omega_r) := \eta(\beta(K), \Omega_r) = \prod_{i=0}^{r-1} \exp(b_{r-1-i,K} \cdot 2\pi \omega_i u_i)
$$

定义 4.10. – 我们为 r = 6 定义一个样本族，

$$
\Omega_6^\varnothing := \left{ \left{\frac{1}{3}, \frac{i+j+k}{\sqrt{3}}\right}, \left{\frac{1}{3}, \frac{i+j+k}{\sqrt{3}}\right}, \left{\frac{1}{6}, \frac{i+j+k}{\sqrt{3}}\right}, \left{\frac{1}{4}, i\right}, \left{\frac{1}{4}, j\right}, \left{\frac{1}{8}, i\right} \right}
$$

图4.7 显示，由 $\Omega_6^\varnothing$ 构成的三进制‐二进制树的最简单的闭合格由两个模块（参见 Wolfrma）组成，具有 144 个连接和 96 个节点。

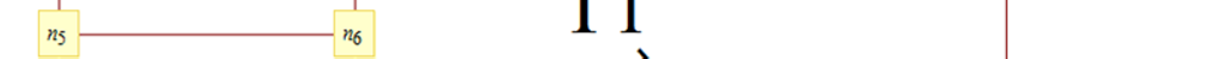
4.4. 扰动容差

定义 4.17. – 我们在每个节点定义一个比特值：

$$
\forall K \in \mathbb{N} \cap [0,2^r[, \quad \forall n_k \in \text{nodes}(\mathcal{T}_{r+1}), \quad \mathcal{B}(n_k) := k \mod 2
$$

根据我们的方法，三元二叉树中的拓扑比特保留了内在几何结构。
超级节点的中心被确定为大小为4的单环。与相邻的单三角形相关联，它们分别形成由比特0、0和1告知信息的三个节点的中心三角形，并且每个节点连接到分别与0、1和1关联的二叉树的第一个节点。因此，每棵树的根由两个不同比特上的二进制码表征，然后各层级分支中的后续节点由0和1标识。三棵6阶二叉树的24片叶子由一个5位标识符[FEM 94]表征。晶格条件方程[4.16]表示，来自相连的三元树的两个相连叶节点的标识符具有通过函数α关联的二进制标识符，该函数引入了冗余信息，从而实现了对干扰的容忍度。

4.5. 结论

在人工智能领域以及神经网络架构方面的研究曾以超金刚石和超立方体结构秘密进行。事实上，鉴于时空的本质与四维几何相关联，空间人工智能即使在时空中也理应依赖于这些几何结构。我们认为图立顿模型值得在这一领域得到研究。

煎饼与超立方体网络、超立方体，特别是交叉超立方体 [TSA 08] 是当前研究的热点，旨在优化通信网络中的可靠性、传输延迟、速率和能耗，尤其是在具有动态拓扑的新网络中。

我们的图顿模型可以被视为混合网络。当大规模基础设施固定时，这类模型显得尤为有趣；仅在小尺度上，网络中的节点会动态地连接或断开。这种行为对应于通过T1变换（如图4.4所示）以及网络结构的局部变化来交换比特。我们认为，物联网的到来以及手机中RFID标签和集成NFC天线的日益普及，将导致混合物理网络的出现。图立顿模型可能在这些新型混合网络的模拟与管理中发挥重要作用。我们的主要成果在于，这些模型定义了一种信息结构，能够同时编码程序与数据，而硬件则由一个局部图算子进行管理，该算子分析周围环境并决定是否执行T1拓扑变换。这种动态图在人工智能和网络优化方面具有广阔的应用前景。

已明确所提出的架构适用于四维神经网络的构建以及三维轨迹的识别。
RFID标签的应用与配备有检测器和定位系统的智能手机动态链接，从而能够处理该信息的时空动态。RFID标签将由我们的超金刚石网络中的空超级节点建模，并在被检测到时激活。该应用的功能将在未来的工作中讨论。