代码随想录算法训练营第 54 天 | 108. 冗余连接、109. 冗余连接II

原创 已于 2025-12-03 15:00:35 修改 · 264 阅读 · 2 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#算法 #数据结构 #java #图 #并查集

于 2025-12-03 14:56:44 首次发布

108. 冗余连接

题目链接

思路：并查集。每添加一条边，就判断这两个节点是否在统一集合。如果是，说明它是冗余的最后一条边，立即返回；否则把这两个节点添加到一个集合中。

只有 1 条冗余边。

拓展：树是一种无向无环图，n 个节点只需要 n - 1 条边就能完全联通。

import java.util.Scanner;

public class Main {
    static int n = 1005;
    static int[] father = new int[n];
    static {
        init();
    }

    static void init() {
        for (int i = 0; i < n; i++) {
            father[i] = i;
        }
    }

    static int find(int a) {
        return father[a] == a ? a : (father[a] = find(father[a]));
    }

    static void join(int a, int b) {
        if (father[a] != father[b]) {
            a = find(a);
            b = find(b);
            father[a] = b;
        }
    }

    static boolean isSame(int a, int b) {
        a = find(a);
        b = find(b);
        return a == b;
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        while (n-- > 0) {
            int s = sc.nextInt();
            int t = sc.nextInt();
            if (isSame(s, t)) {
                System.out.println(s + " " + t);
                return;
            } else {
                join(s, t);
            }
        }
    }
}

109. 冗余连接II

题目链接

leetcode 685

分为两大类情况：

  • 存在入度为 2 的节点——判断删哪条边能成为一颗有向树。
    • 可以任意删除一条（优先删除后添加的）（情况 1）
    • 必须删除特定的一条（情况 2）
  • 入度全部为 1，退化成和 108. 冗余连接 一样（情况 3）

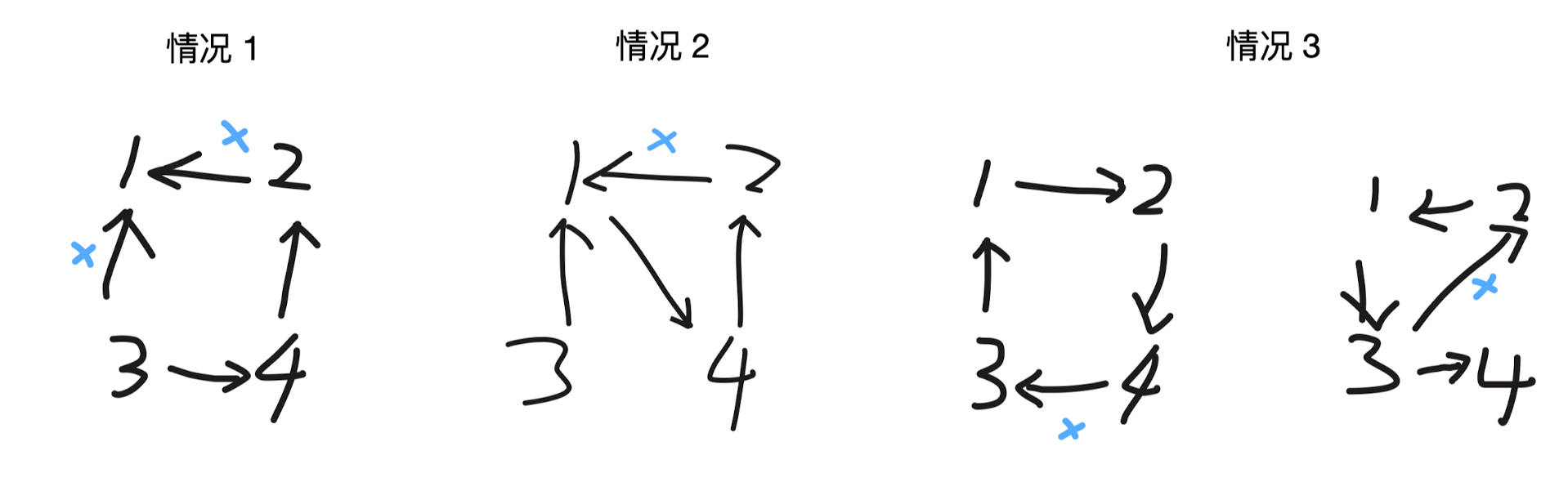
在这里插入图片描述

自己写的：

import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;

public class Main {
    static int n = 1005;
    static int[] father = new int[n];
    static {
        init();
    }

    static void init() {
        for (int i = 0; i < n; i++) {
            father[i] = i;
        }
    }

    static int find(int a) {
        return father[a] == a ? a : (father[a] = find(father[a]));
    }

    static void join(int a, int b) {
        if (father[a] != father[b]) {
            a = find(a);
            b = find(b);
            father[a] = b;
        }
    }

    static boolean isSame(int a, int b) {
        a = find(a);
        b = find(b);
        return a == b;
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();

        List<int[]> edge = new ArrayList<>();
        int[] inDegree = new int[n + 1]; // 统计入度为 2 的节点

        for (int i = 0; i < n; i++) {
            int s = sc.nextInt();
            int t = sc.nextInt();
            edge.add(new int[] {s, t});
            inDegree[t]++;
        }
        
        int size = 0; // 统计入度为 2 的节点个数
        int v = 0;

        for (int i = 1; i < n + 1; i++) {
            if (inDegree[i] == 2) {
                size++;
                v = i;
                break;
            }
        }

        if (size > 0) {
            List<int[]> deleteEdge = new ArrayList<>(); // 哪两条边出度为 2
            List<Integer> index = new ArrayList<>(); // 入度为 2 的边在 edge 中的序号是多少
            for (int i = 0; i < n; i++) {
                if (edge.get(i)[1] == v) {
                    deleteEdge.add(edge.get(i));
                    index.add(i);
                }
            }

            if (isTreeAfterDelete(edge, index.get(1))) { // 优先删后添加的边
                System.out.println(deleteEdge.get(1)[0] + " " + deleteEdge.get(1)[1]);
            } else {
                System.out.println(deleteEdge.get(0)[0] + " " + deleteEdge.get(0)[1]);
            }
        } else {
            for (int i = 0; i < n; i++) {
                int s = edge.get(i)[0];
                int t = edge.get(i)[1];
                if (isSame(s, t)) {
                    System.out.println(s + " " + t);
                    return;
                } else {
                    join(s, t);
                }
            }
        }
    }

    private static boolean isTreeAfterDelete(List<int[]> edge, int index) {
        for (int i = 0; i < edge.size(); i++) {
            if (i == index) {
                continue;
            }
            int s = edge.get(i)[0];
            int t = edge.get(i)[1];
            if (isSame(s, t)) {
                return false;
            } else {
                join(s, t);
            }
        }
        return true;
    }
}

优化后的代码：
把

        int size = 0; // 统计入度为 2 的节点个数
        int v = 0;
        
        for (int i = 1; i < n + 1; i++) {
            if (inDegree[i] == 2) {
                size++;
                v = i;
                break;
            }
        }

优化成：

        List<Integer> indexOfDeleteEdge = new ArrayList<>(); // 入度为 2 的边在 edge 中的序号是多少

        for (int i = 0; i < n; i++) {
            if (inDegree[edge.get(i)[1]] == 2) { // 最精妙的地方，不是直接判断 inDegree[i] == 2，那样只会添加 1 次，表示哪个节点入度为 2
                indexOfDeleteEdge.add(i); // 应该会添加 2 次。保证了后添加的边在后边。
            }
        }

import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;

public class Main {
    static int n = 1005;
    static int[] father = new int[n];
    static {
        init();
    }

    static void init() {
        for (int i = 0; i < n; i++) {
            father[i] = i;
        }
    }

    static int find(int a) {
        return father[a] == a ? a : (father[a] = find(father[a]));
    }

    static void join(int a, int b) {
        if (father[a] != father[b]) {
            a = find(a);
            b = find(b);
            father[a] = b;
        }
    }

    static boolean isSame(int a, int b) {
        a = find(a);
        b = find(b);
        return a == b;
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();

        List<int[]> edge = new ArrayList<>();
        int[] inDegree = new int[n + 1]; // 统计入度为 2 的节点

        for (int i = 0; i < n; i++) {
            int s = sc.nextInt();
            int t = sc.nextInt();
            edge.add(new int[] {s, t});
            inDegree[t]++;
        }

        List<Integer> indexOfDeleteEdge = new ArrayList<>(); // 入度为 2 的边在 edge 中的序号是多少

        for (int i = 0; i < n; i++) {
            if (inDegree[edge.get(i)[1]] == 2) { // 最精妙的地方，不是直接判断 inDegree[i] == 2，那样只会添加 1 次，表示哪个节点入度为 2
                indexOfDeleteEdge.add(i); // 应该会添加 2 次。保证了后添加的边在后边。
            }
        }

        if (indexOfDeleteEdge.size() > 0) {
            int index1 = indexOfDeleteEdge.get(0); // 待删除的边在 edge 中的索引
            int index2 = indexOfDeleteEdge.get(1);

            int s1 = edge.get(index1)[0];
            int t1 = edge.get(index1)[1];

            int s2 = edge.get(index2)[0];
            int t2 = edge.get(index2)[1];

            if (isTreeAfterDelete(edge, index2)) { // 优先删后添加的边
                System.out.println(s2 + " " + t2);
            } else {
                System.out.println(s1 + " " + t1);
            }
        } else { // 不删任何边，把造成不能成为有向树的冗余边找出来
            for (int i = 0; i < n; i++) {
                int s = edge.get(i)[0];
                int t = edge.get(i)[1];
                if (isSame(s, t)) {
                    System.out.println(s + " " + t);
                    return;
                } else {
                    join(s, t);
                }
            }
        }
    }

    // 删了这条边之后，能否成为有向树
    private static boolean isTreeAfterDelete(List<int[]> edge, int index) {
        for (int i = 0; i < edge.size(); i++) {
            if (i == index) {
                continue;
            }
            int s = edge.get(i)[0];
            int t = edge.get(i)[1];
            if (isSame(s, t)) {
                return false;
            } else {
                join(s, t);
            }
        }
        return true;
    }
}
代码随想录算法训练营第56天 | 108.冗余连接、109.冗余连接II
Athenaand的博客
09-11 254
第56天，继续加油。
代码随想录算法训练营第56天 | 108.冗余连接、109.冗余连接 II
Alive1218的博客
03-31 177
109.冗余连接 II。
代码随想录算法训练营Day54 | 108.冗余连接、109.冗余连接 II
Harryline的博客
02-14 221
代码随想录算法训练营Day54 | 108.冗余连接、109.冗余连接 II
代码随想录算法训练营第五十六天 | 108.冗余连接 109.冗余连接II
qq_46651958的博客
03-24 1865
，这说明在两条边都可以删除的情况下，要删顺序靠后的边！我们来想一下 有向树的性质，如果是有向树的话，只有根节点入度为0，其他节点入度都为1（因为该树除了根节点之外的每一个节点都有且只有一个父节点，而根节点没有父节点）。所以情况一：如果我们找到入度为2的点，那么删一条指向该节点的边就行了。如图：找到了节点3 的入度为2，删 1 -> 3 或者 2 -> 3。选择删顺序靠后便可。但 入度为2 还有一种情况，情况二，只能删特定的一条边，如图：
代码随想录算法训练营第五十六天|108.冗余连接 109.冗余连接II
aaaaaaaaaaaaay的博客
09-30 175
具体的方法是每经过一条边，设两个节点为u，v，首先判断v的父节点是否是v（注意这里是父节点而不是祖先节点），如果不是v，说明之前已经有一个父节点，说明同时出现了两个父节点，记录这个位置。如果还是v，那就将u变为v的父节点，之后判断u和v是否是同一集合，是同一集合就代表已经成环，同样记录。之后判断如果不存在两个父节点，那么冗余边一定是导致成环，就输出成环位置的边，存在再判断是否成环，如果有环那就输出不成环的另一条冗余边（因为只有一条冗余边，两个问题肯定是同一条边导致的），不成环就输出后来的那条。
代码随想录算法训练营第六十一天 | 108. 冗余连接 109. 冗余连接II
ZAcoooo的博客
03-10 277
状态：AC。
代码随想录算法训练营第56天| 108. 冗余连接、109. 冗余连接II
2301_76253115的博客
02-26 239
写完一直提交通不过 发现是倒数第三行之前复制过来没改成1 我真服了。学习链接：​​​​​​​。依然是并查集的应用。
代码随想录算法训练营第六十天| 108. 冗余连接、109. 冗余连接II
07-09 1271
3. 第 “2” 步中, 如果存在入度为 2 的节点, 删除进入该节点的其中一条边后如果不存在环, 则说明删除有效, 否则则需要删除另外一条边. 而判断环需要使用到并查集. 因为如果存在环的话, 连接尾首的那条边, 在并查集中就会发现首尾两个节点已经在集合中, 并返回发现环.输入一个有向图，该图由一个有着 n 个节点(节点编号 从 1 到 n)，n 条边，请返回一条可以删除的边，使得删除该条边之后该有向图可以被当作一颗有向树。输出一条可以删除的边，若有多条边可以删除，请输出标准输入中最后出现的一条边。
代码随想录算法训练营第六十天|108. 冗余连接，109. 冗余连接II
weixin_43270226的博客
11-11 359
该树除了根节点之外的每一个节点都有且只有一个父节点，而根节点没有父节点。输入一个有向图，该图由一个有着 n 个节点(节点编号 从 1 到 n)，n 条边，请返回一条可以删除的边，使得删除该条边之后该有向图可以被当作一颗有向树。现在在这棵树上的基础上，添加一条边（依然是n个节点，但有n条边），使这个图变成了有环图，如图。后续 N 行，每行输入两个整数 s 和 t，代表这是 s 节点连接并指向 t 节点的单向边。输出一条可以删除的边，若有多条边可以删除，请输出标准输入中最后出现的一条边。输出一条可以删除的边。
代码随想录算法训练营第三天| 203.移除链表元素 707.设计链表| 206.反转链表
kkksij的博客
10-28 1174
建议： 本题最关键是要理解 虚拟头结点的使用技巧，这个对链表题目很重要。思路：1.直接使用原来的链表进行删除操作。 2.设置一个虚拟头结点在进行删除操作题目链接：. - 力扣（LeetCode）视频链接：手把手带你学会操作链表 | LeetC de：203.移除链表元素_哔哩哔哩_bilibili文章链接：手把手带你学会操作链表 | LeetCode：203.移除链表元素_哔哩哔哩_bilibili具体实现：定义一个cur = head 的结点，遍历链表，每次遍历时 cur.val 和
代码随想录算法训练营第一天 - 704. 二分查找
05-08
代码随想录算法训练营第一天 - 704. 二分查找
代码随想录算法训练营第一天- 977.有序数组的平方 ， 209.长度最小的子数组，59.螺旋矩阵II
10-12
代码随想录算法训练营第一天- 977.有序数组的平方 ， 209.长度最小的子数组，59.螺旋矩阵II
【模式识别与机器学习（8）】主要算法与技术（下篇：高级模型与集成方法）之 元学习与集成方法：组合多个学习器来提高整体性能
hiliang521的博客
12-02 877
【模式识别与机器学习（8）】主要算法与技术（下篇：高级模型与集成方法）之 元学习
Leetcode 68 搜索插入位置 | 寻找比目标字母大的最小字母
im_AMBER的博客
12-04 1021
你的错误逻辑正确逻辑找到 target 时返回 mid-1找到 target 时，继续向右查找（因为需要「大于」target 的最小字符）target <letters [mid] 时，mid 是候选，需保留，right=mid（左闭右开）或不立即排除 mid循环结束直接返回 letters [0]循环结束后，先判断 left 是否越界：越界则返回 letters [0]，否则返回 letters [left]初始right的取值与「越界判断」不匹配；
完全背包 vs 多重背包的优化逻辑
布心老混子
12-02 328
做题时想到完全背包是可以转化成多重背包的，那么多重背包需要二进制优化，完全背包需要吗？
欧几里得距离算法-相似度
weixin_45609702的博客
12-04 182
本文介绍了一个计算欧几里得距离的Java方法。该方法接收两个Double数组作为输入，通过计算对应元素差值的平方和再开方，返回两个数组之间的欧几里得距离值。当输入数组长度不一致时，方法会返回0作为默认值。欧几里得距离算法常用于比较两个数组之间的相似度，是数据分析和机器学习中的基础距离度量方法。
C++ ⼀级 2024 年 03 ⽉
weixin_46669997的博客
12-05 21
当 N 为9, 6, 3, 0时，满足条件 N % 3 == 0，因此它们被输出并跟随一个 #。要注意的是，字符串“a+1= ”最后有一个空格，因而输出的内容是：a+1= 2，答案为A。输入21，21%3的结果为0，进入if的分支，因而第4行代码可以被执行。19.【判断题】C++表达式 “10”*2 执行时将报错，因为 “10” 是字符串类型而2是整数类型，它们数据类型不同，不能在一起运算。Cout后面有两个<<，第1个输出字符串5%2=，第2个输出算术运算“5%2”的结果，为1，答案为D。
浅谈：快递物流与算法的相关性（五）
最新发布
Duoya1105的博客
12-05 131
NP-C 的英文全称是 Non-deterministic Polynomial Complete，即多项式复杂程度的非确定性问题。简单的写法是NP=P？，问题就在这个问号上，到底有没有让NP=P的算法，或是如何证明NP≠P。启发式算法的思想是：在不断解决问题的过程中寻找解决问题的最优方案。再举一个通俗的例子：当我们用数字密码解锁手机时，如果我们不知道密码是多少，必须将所有的数字组合依次尝试。这听起来像是一句废话，如果将它抽象一点的表述，就是：能用电脑快速验证一个解的问题，是否也能够用电脑快速地求出解。
[优选算法专题十.哈希表 ——NO.55~57 两数之和、判定是否互为字符重排、存在重复元素]
2401_83386596的博客
12-03 679
两数之和问题的最优解法采用哈希表实现O(n)时间复杂度，通过存储元素值与下标的映射关系，快速查找互补值。字符重排判定问题通过单哈希数组统计字符出现次数，先加后减并实时校验，确保字符种类和数量完全一致。存在重复元素问题使用哈希集合检测重复元素，遍历数组时检查元素是否已存在于集合中。三种解法均利用哈希结构优化查找效率，将时间复杂度从暴力解法的O(n²)降至O(n)，是典型空间换时间策略的工业级实现。
代码随想录算法训练营第五天
02-17
### 关于代码随想录算法训练营第五天学习内容 #### 动态规划入门 动态规划是一种通过把原问题分解为相对简单的子问题的方式来求解复杂问题的方法。在第五天的学习中，重点在于理解并掌握动态规划的核心概念及其应用。 #### 解决斐波那契数列问题 斐波那契数列是一个经典的例子来介绍动态规划的思想。对于给定的n值，计算第n项斐波那契数值可以采用自底向上的方法构建解决方案[^1]： ```python def fib(n): if n <= 0: return 0 elif n == 1: return 1 dp = [0] * (n + 1) dp[1] = 1 for i in range(2, n + 1): dp[i] = dp[i - 1] + dp[i - 2] return dp[n] ``` 此实现方式避免了重复计算相同的子问题，从而提高了效率。 #### 攀爬楼梯问题 另一个典型的应用场景是攀爬楼梯问题，假设每次可以选择走一步或两步，则到达第n阶的不同路径总数也可以利用动态规划解决: ```python def climbStairs(n): if n == 1 or n == 2: return n dp = [0] * (n + 1) dp[1], dp[2] = 1, 2 for i in range(3, n + 1): dp[i] = dp[i - 1] + dp[i - 2] return dp[-1] ``` 上述两个案例展示了如何运用动态规划技巧有效地解决问题，并且强调了状态转移方程的重要性以及边界条件处理。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值