CS61B - Lec28 - Intro to Graphs

今天学习了新的结构——Graph，是更广义上的Tree（Tree∈Graph)。

Trees and Traversals

这一节讲了之前提到的Tree的遍历方式（Traversals)——preorder, inorder, postorder。具体意思就是根节点的三种遍历顺序，最先，中间以及最后。
先打根节点（preOrder)：

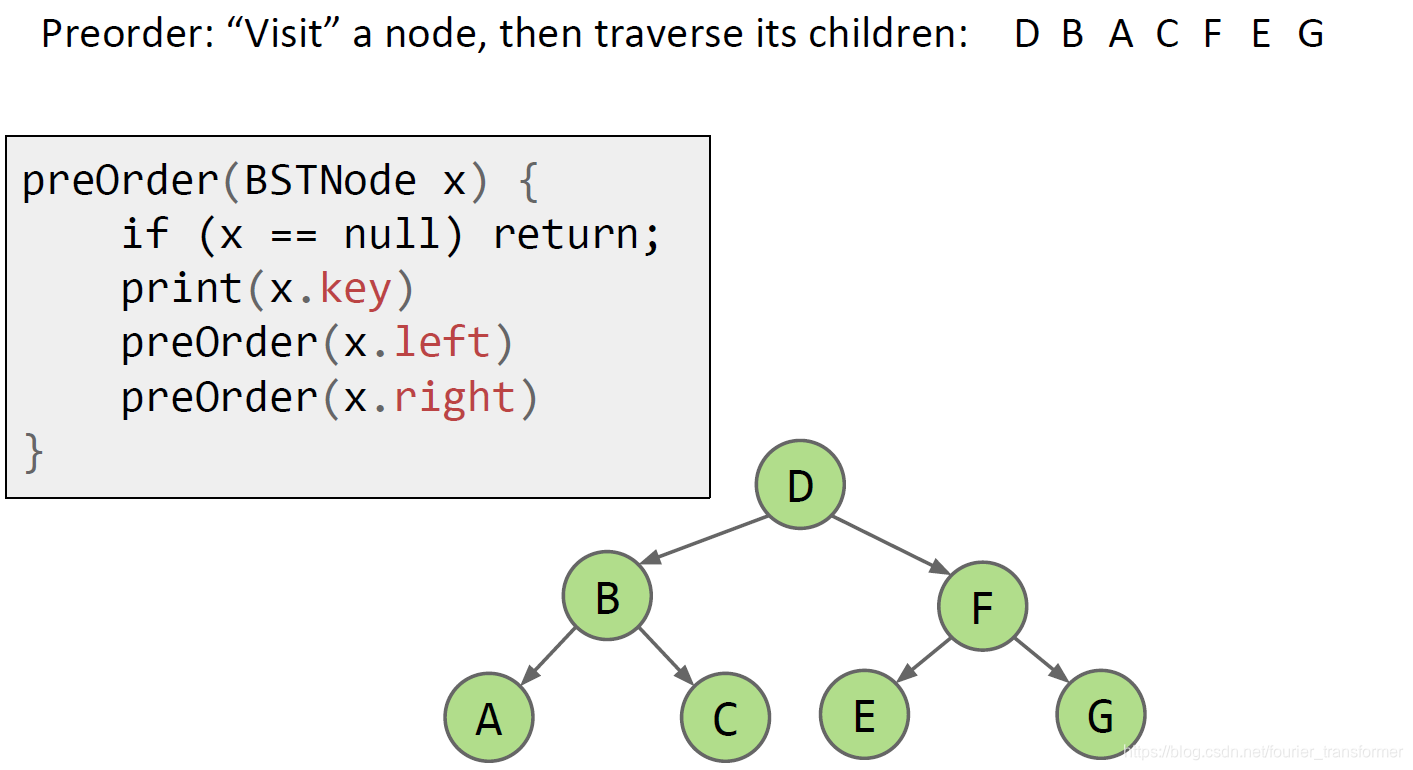
先打左节点（inOrder)：

最后打根节点（postOrder):

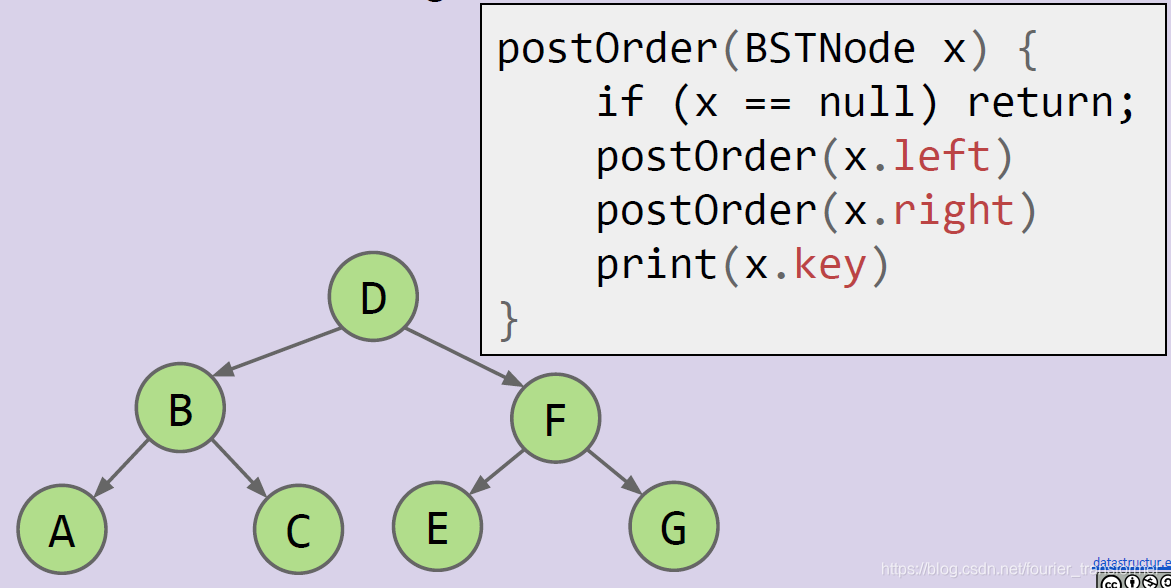
树形结构适合文件管理，如下图，递归的遍历方式可以很方便的实现各个文件夹统计文件总数的功能。

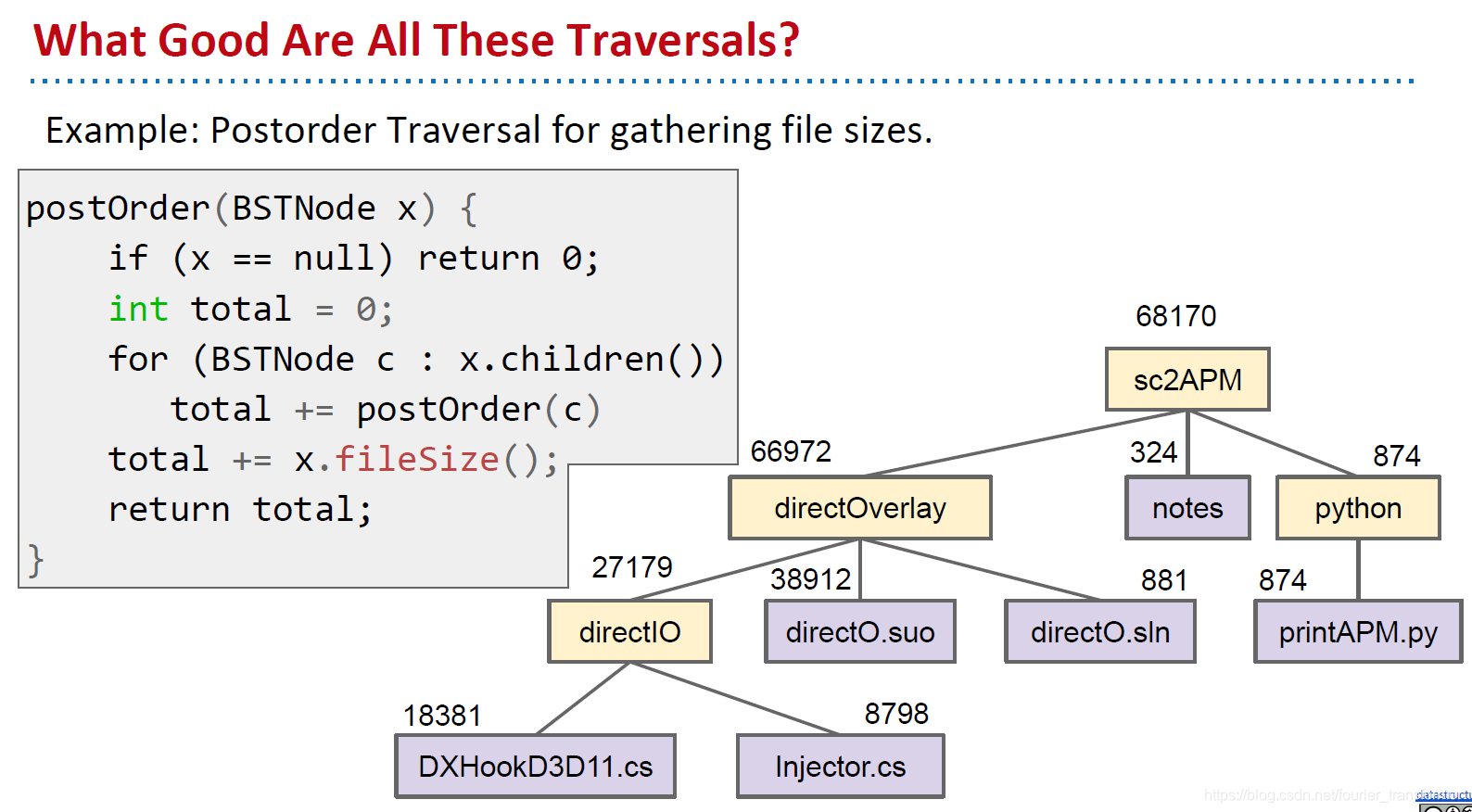
Graphs

前面说过了，Graphs是更广义上的Tree，Tree属于Graph的一部分。Tree必须满足两点之间有且只有一条路径，而Graph可以包含cycle，并且两点之间还可以不相连。