DiffPool

最新推荐文章于 2025-09-24 13:34:17 发布
原创 最新推荐文章于 2025-09-24 13:34:17 发布 · 1k 阅读 · 7 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#深度学习

Paper : Hierarchical Graph Representation Learning with Differentiable Pooling
Code :

摘要

对于Graph Classification 任务来说，GNN的最后一步需要关注图数据的全局信息，既包含图的结构信息，也包含各个节点的属性信息。如果采用一次性全局池化的方法聚合点上的特征表示，并没有将图的结构考虑进去，而且可能在节点重编号后聚合的结果会发生改变，也就是说聚合过程中依赖节点顺序。在CNN模型中，通常采用的做法是通过层次化池化机制来逐渐提取全局信息，作者仿照CNN提出了一种层次化图聚类的方式，支持添加到GNN模型中进行端到端的学习。
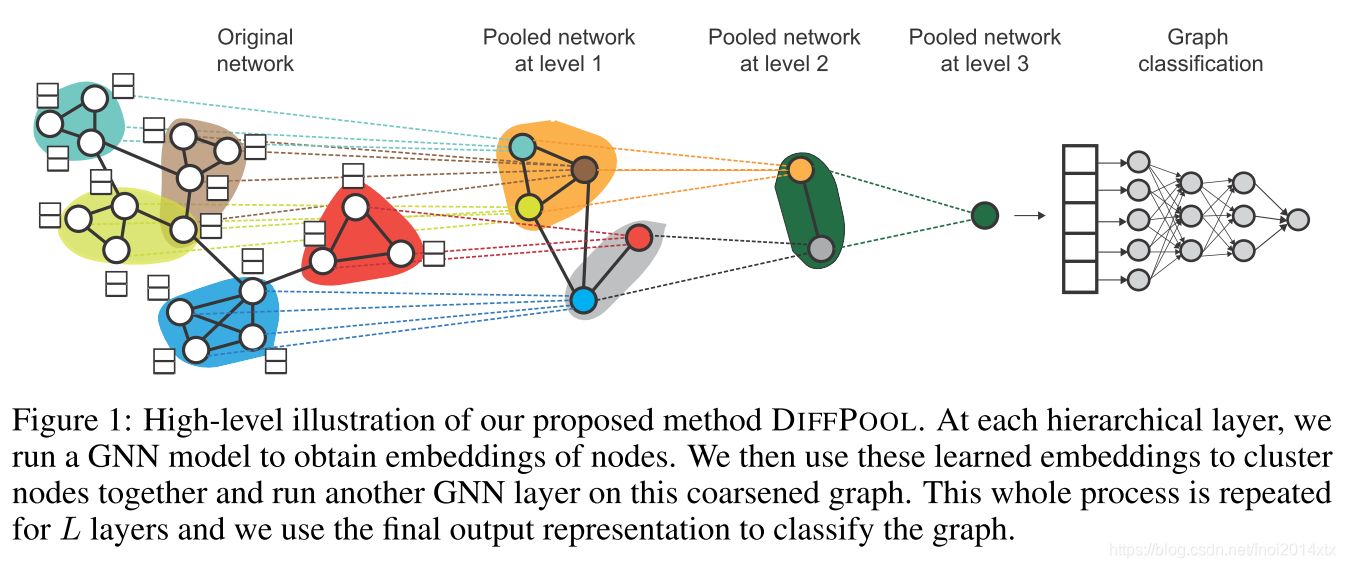
在这里插入图片描述
每层将该层的节点映射到若干个cluster中，作为下一层输入的节点。

定义

定义图 G G G 表示为 ( A , F ) (A,F) (A,F) ，其中 A ∈ { 0 , 1 } n × n A\in\{0,1\}^{n\times n} A∈{ 0,1}n×n 表示邻接矩阵， F ∈ R n × d F\in \mathbb R^{n\times d} F∈Rn×d 表示节点的特征矩阵。图分类任务定义为学习一个映射 f : G → Y f : \mathcal G \rightarrow \mathcal Y f:G→Y，这需要首先学习图的整体特征表示，即 f ′ : G → R D f' : \mathcal G\rightarrow \mathbb R^{D} f′:G→RD

图神经网络的数学表示为

H ( k ) = M ( A , H ( k − 1 ) ; θ ( k ) ) H^{(k)} = M(A,H^{(k-1)};\theta^{(k)}) H(k)=M(A,H(k−1);θ(k))

其中， H ( k ) ∈ R n × d H^{(k)}\in \mathbb R^{n\times d} H(k)∈Rn×d， H ( 0 ) = F H^{(0)} = F H(0)=F，一种常见的GNN模型表示为

H ( k ) = ReLU ( D ~ − 1 2 A ~ D ~ − 1 2 H ( k − 1 ) W ( k − 1 ) ) H^{(k)} = \text{ReLU}(\widetilde D^{-\frac{1}{2}}\widetilde A\widetilde D^{-\frac{1}{2}}H^{(k-1)}W^{(k-1)}) H(k)=ReLU(D −21​

最低0.47元/天 解锁文章
DIFFPOOL - Hierarchical Graph Representation Learning with Differentiable Pooling NIPS 2018
知行合一，止于至善
01-07 1606
文章目录1 相关介绍相关概念背景介绍模型简介2 相关工作3 DIFFPOOL：可微的pooling方法3.1 问题定义图神经网络堆叠GNNs和pooling层3.2 通过学习聚类分配矩阵来进行可微的poolingQ1: 怎样学习聚类分配矩阵S？Q2: 假定聚类分配矩阵已存在，如何进行Pooling？Permutation invariance排列不变性3.3 Auxiliary Link Prediction Objective and Entropy Regularization4 实验数据集模型配置Ba
图池化经典之作: 18NIPS DiffPool
weixin_45519842的博客
02-11 754
作者:张楚珩单位:清华大学交叉信息研究院原文链接:https://zhuanlan.zhihu.com/p/106214278DiffPool: Differentiable Po...
PyTorch Geometric图池化技术：TopK池化、DiffPool等高级技术详解
gitblog_00883的博客
09-24 515
图池化（Graph Pooling）是图神经网络（GNN）中的关键操作，旨在通过保留重要节点和压缩图结构来降低计算复杂度，同时维持图的关键语义信息。随着图深度学习的发展，TopK池化、DiffPool等高级池化技术逐渐成为处理大规模图数据的核心工具。本文将深入解析PyTorch Geometric（PyG）中实现的主流图池化算法原理、实现细节及应用场景，并通过代码示例展示如何在实际任务中应用这些技...
论文笔记--Hierarchical Graph Convolution Networks for Traffic Forecasting
chenxino的博客
10-03 1396
Hierarchical Graph Convolution Networks for Traffic Forecasting (AAAI 21) Summary 作者提出了一种新的层次图卷积网络(HGCN)，通过操作微观和宏观交通图进行交通预测。 Problem Definition 目前基于GCN的交通预测方法都忽略了交通系统的自然层次结构，既包括道路网络的基本微观层，也包括路网的宏观层，区域或社区的特征和信息在传统的交通规划或宏观特征分析转化理论中发挥着重要作用。 问题定义 与一般的交通预测问题相同
DIFFPOOL（Hierarchical Graph Representation）
weixin_40248634的博客
12-07 1227
Hierarchical Graph Representation Learning with Differentiable Pooling动机核心思想图神经网络可微分池化层 Differentiable Pooling) 论文链接：https://arxiv.org/pdf/1806.08804.pdf 一些概念：置换矩阵：每个行以及每个列都只有一个1的矩阵，其可以看做是单位阵经过行的交换而生成...
DiffPool 笔记 自用
qq_40515250的博客
04-21 2867
DiffPool 笔记 自用DiffPool 可微池化的层次图表示学习相关概念背景堆叠GNNs和pooling层Diff pool正则化实验 DiffPool 可微池化的层次图表示学习 转载： 版权声明：本文为优快云博主「不务正业的土豆」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。 原文链接：https://blog.youkuaiyun.com/yyl424525/article/details/103307795 Hierarchical Graph Representati
[Graph Classification] DiffPool 论文笔记
ilikevegetable的博客
12-06 922
文章目录[Graph Classification] DiffPoolIntroductionAlgorithm [Graph Classification] DiffPool DiffPool是一种可微的图pooling方法，可以生成图的层次表示，并捕捉图的层次结构信息，并且可以结合到很多的GNN模型中。   Introduction DiffPool的方法如上图所示，大致流程为： 通过GNN学习图中节点的embeddings，通过另一个GNN学习节点的分配矩阵 通过分配矩阵，将初始矩阵pooling
DIFFPOOL | 利用可微分池化层构建层级图神经网络
paper_reader的博客
04-23 4227
Ying,Zhitao,etal."Hierarchicalgraphrepresentationlearningwithdifferentiablepooling."Advancesinneuralinformationprocessingsystems.2018. 阅读更多，欢迎关注公众号：论文收割机（paper_reader） 因为排版问题，很多图片和...
DiffPool: Hierarchical Graph Representation Learning with Differentiable Pooling
todoooooo的博客
06-02 898
本文提出了一种分层的图池化机制DiffPool，通过将原始图的部分节点映射成粗粒度图上的一个节点模型能够学习到图的层级结构，在池化多次后将图映射成一个节点，进而得到整张图的表示。 本文被NIPS2018接收，地址：Hierarchical Graph Representation Learning with Differentiable Pooling Motivation 在有机分子中，人们希望能够编码局部的分子结构（原子间的化学键）以及图的粗粒度结构（代表分子功能的结构单元），但当前的GNN无法以分层的
[DIFFPOOL] - Hierarchical Graph Representation Learning with Differentiable Pooling 图分类 NeurIPS 2018
热门推荐
知行合一，止于至善
11-29 1万+
文章目录1 相关介绍相关概念背景介绍模型简介2 相关工作3 DIFFPOOL：可微的pooling方法3.1 问题定义图神经网络堆叠GNNs和pooling层3.2 Differentiable Pooling via Learned AssignmentsPooling with an assignment matrixLearning the assignment matrixPermutat...
探秘DiffPool：新型图神经网络库，解锁数据集挖掘新可能
gitblog_00050的博客
04-18 660
探秘DiffPool：新型图神经网络库，解锁数据集挖掘新可能 是一个用于图神经网络（GNN）的开源项目，由 Rex Ying 创建并维护。它主要解决了传统GNN在处理变结构图数据时的局限性，通过对节点聚类实现层次化的图池化操作，为深度学习在复杂异构数据上的应用提供了新的可能。 项目简介 DiffPool的核心在于其引入了一种可微分的池化层，这使得模型能够自适应地学习不同图实例的最优节点聚类方案。通...
DiffPool（Differentiable Pooling）数学公式解析
Never Give Up
03-19 807
DiffPool（Differentiable Pooling）是一种。DiffPool 的目标是。，可以端到端地训练。
【GNN】Diff Pool：网络图的层次化表达
阿泽的学习笔记
06-09 1669
今天学习的是斯坦福大学的同学 2018 年的工作《Hierarchical Graph Representation Learning with Differentiable Pooling》，目前共有 140 多次引用。 目前，GNN 在图分类任务中的处理方法本质上是平面的（Flat），无法学习图形的层次化表达。对于一个包含多个标签的图来说，传统的方法都是为图中每个节点生成一个 Embedding 向量，然后利用这些 Embedding 向量来做全局池化或者输入到 MLP 中来预测图标签，但这种方法忽视了
指标实现层级_DIFFPOOL | 利用可微分池化层构建层级图神经网络
weixin_35261775的博客
12-31 341
Ying,Zhitao,etal."Hierarchicalgraphrepresentationlearningwithdifferentiablepooling."Advancesinneuralinformationprocessingsystems.2018.引言现有的图神经网络大多数是平面化的(flat)学习方式，也就是所有网络信息的传播(pr...
图分类《Hierarchical Graph Representation Learning with Differentiable Pooling》阅读笔记
weixin_37936515的博客
03-11 1447
图分类《Hierarchical Graph Representation Learning with Differentiable Pooling》阅读笔记 Abstract 对于graph neural networks (GNNs)，大体上分三种任务：Node Classification，Link Prediction和 Graph Classification。本文关注的是Graph C...
基于差分池化的分层图表示方法概述
Startapi的博客
10-27 394
声明 本篇论文的主要内容来自于斯坦福大学的博士生Rex Ying，论文名称为：Hierarchical Graph Representation Learning withDifferentiable Pooling。论文地址:点击下载。但需要说明的是本篇文正并不是对论文的翻译，书中大部分内容是作者对论文理解，当然可能个人水平有限，中间难免会出现一些错误，如若发现恳请指出，不胜赐教。 背景 近...
Hierarchical Graph Network for Multi-hop Question Answering 论文笔记
qq_42791848的博客
02-20 2171
Hierarchical Graph Network for Multi-hop Question Answering 论文笔记 2020 EMNLP，Microsoft 365， 这篇文章所提出的层级图模型是在leaderboard上排名比较高的一个模型。 Overview 这篇文章同样是引入图表示学习来做多跳推理，但是本文在建图上做了改进和创新，提出Hierarchical Graph。作者认为之前基于图表示学习的方法有两个不足：一是图只被用来预测答案，没有充分地去寻找supporting fact；二
Hierarchical graph representations in digital pathology
NanXian Lin的博客
03-22 4014
Author: Pushpak Pati Publication: Medical image analysis Introduction 组织标本的癌症诊断、预后和治疗反应预测高度依赖表型和构成组织实体的拓扑分布。因此，适当的组织代表编码组织实体是计算机辅助癌症患者护理的当务之急。为此，有几种方法利用细胞图，捕捉细胞微环境，以描绘组织。这允许利用图论和机器学习将组织表示映射到组织功能，并量化他们的关系。虽然细胞信息是至关重要的，但它是不完整的综合表征复杂的组织结构。在此，他们将组织作为多种类型的组织
图分类之Hierarchical Graph Differentiable Pooling （下）
chumingqian的博客
05-30 1068
是为图结构数据设计的神经网络模型。它通过结合分层池机制扩展了传统图卷积网络（GCN）的功能。这种池化机制通过逐步减少节点数量，同时保留图的整体结构，帮助网络处理大型且复杂的图。通过引入软池机制来增强 GCN，该机制允许在大型复杂图中进行分层表示学习。它结合了多层图卷积和池化来创建输入图的鲁棒、多尺度表示，使其适用于各种图分类和预测任务。链接预测正则化进一步增强了其在池化过程中保持图的结构完整性的能力。该模型从传统的 GCN 层开始，将图卷积应用于输入节点特征。
TMS-GNN算法模型系统框架图
最新发布
10-14
<think>首先，用户的问题是：“我想查找TMS - GNN算法模型系统的框架图 请问TMS - GNN算法模型系统的框架图” 用户提到了“TMS - GNN算法模型系统的框架图”。TMS 可能指的是 Transportation Management System（运输管理系统），因为它与物流相关。GNN 是图神经网络。所以，整体上下文是关于智能物流、GNN 在物流中的应用。 回顾系统级指令： - 所有行内数学表达式使用 $...$ 格式。 - 独立公式使用 $$...$$ 格式并单独成段。 - LaTeX语法正确。 - 使用中文回答。 - 生成相关问题。 - 回答中引用的段落末尾自然地添加引用标识。 用户可见层： - 回答结构清晰，逐步解决问题。 - 保证回答真实可靠。 现在，分析用户的查询：用户想查找TMS - GNN算法模型系统的框架图。意思是用户想看到这个框架的图解或描述。 在提供的引用中： - 引用[1] 讨论智能物流、GNN 的价值、AI应用架构师的角色。 - 引用[2] 提到DiffPool，一种GNN方法，用于图聚类。 - 引用[3] 讨论深度学习在物流中的应用，如路线预测和路径优化。 - 引用[4] 提到机器人系统中的回环检测等。 这些引用没有直接提供一个名为“TMS - GNN算法模型系统”的具体框架图。因此，我需要基于上下文推断可能的框架。 从引用[1]：“支撑GNN的AI平台需要覆盖‘数据→图处理→模型→应用’全链路”。这给出了一个高层次的框架： 1. 数据：收集物流数据（如节点、边）。 2. 图处理：构建图结构。 3. 模型：应用GNN（如GCN）。 4. 应用：部署到实际业务（如物流优化）。 另外，引用[3]提到路径优化应用PPO强化学习算法，动态路由决策响应时间<3秒。GNN 可能被用于构建图表示。 TMS 是 Transportation Management System，通常涵盖运输计划、执行、优化等。结合GNN，可能用于建模物流网络（如节点表示仓库、边表示路径）。 因此，我可以构建一个合理的框架图描述。 回答结构： 1. **解释TMS-GNN的含义**：简要说明TMS是什么，GNN在其中的角色。 2. **描述框架图**：基于通用GNN框架和物流应用，描述系统框架。 3. **提供图解或文字描述**：由于是文本，用文字描述框架的组成部分。 4. **引用相关信息**：自然地添加引用标识。 5. **生成相关问题**：结尾生成相关问题。 框架描述： - 输入层：物流数据（如订单、车辆、位置）。 - 图构建层：将数据转换为图（节点：位置/仓库；边：路径距离/时间）。 - GNN模型层：应用GNN进行学习（如节点分类、链接预测）。 - 输出层：优化决策（如路径规划、ETA预测）。 - 集成应用：嵌入到TMS软件中。 基于引用[1]的结构： - 数据→图处理→模型→应用 具体化： 1. 数据采集：传感器、订单系统数据。 2. 图处理：构建邻接矩阵 $A$ 和特征矩阵 $Z$。 3. GNN模型：如GCN、DiffPool（引用[2]）。 4. 应用：实时路由优化、预测。 使用LaTeX格式： - 行内数学表达式用 $...$，例如节点特征 $Z^{(l)}$。 - 独立公式用 $$...$$，但框架图不是数学公式，所以可能用文字或列表描述。 生成相关问题： - 类似于示例，生成3-4个相关问题。 确保中文回答。 最终回答大纲： 1. 引言：解释TMS-GNN框架。 2. 框架描述：用文本或伪代码描述各层。 3. 引用：在相关部分添加引用。 4. 相关问题：结尾生成。 </think>### TMS-GNN算法模型系统的框架图解释 根据您的查询，您想查找“TMS-GNN算法模型系统”的框架图。TMS（Transportation Management System，运输管理系统）是一种用于优化物流运输的软件系统，而GNN（Graph Neural Network，图神经网络）则用于建模物流网络的复杂关系（如节点表示仓库或配送点，边表示运输路径）。结合两者，TMS-GNN系统利用GNN处理图结构数据，实现对物流网络的智能优化（如路径规划、资源调度）。在智能物流中，GNN能有效将“关系成本”转化为“竞争优势”，而AI平台需覆盖“数据→图处理→模型→应用”全链路[^1]。 由于文本形式无法直接生成图像，我将基于相关引用和行业知识，为您描述一个典型的TMS-GNN框架图结构（这是一个通用化描述，适用于物流优化场景）。框架图通常分为四层：**数据层、图处理层、GNN模型层和应用层**。每个层级的输入、处理和输出如下所述（使用文字和伪代码描述）。 #### TMS-GNN算法模型系统的框架结构 框架图的核心逻辑是：物流原始数据被转换为图结构，GNN模型从中学习并输出优化决策，最终集成到TMS中实现业务应用。以下是详细分层描述（基于引用[1]的全链路概念）： 1. **数据层（输入层）**： - **功能**：收集物流原始数据，包括订单信息、车辆位置、路径距离、时间窗约束等。这些数据通常是结构化和非结构化的混合。 - **输入示例**：订单数据库（如起点、终点、货物量）、IoT传感器数据（如车辆位置）、历史运输记录。 - **输出**：原始数据矩阵，例如节点特征向量 $X$ 和边权重 $W$。 - **关键技术**：数据预处理（清洗、归一化），引用[3]提到在路径优化中需考虑多式联运和新能源充电约束[^3]。 2. **图处理层（图构建层）**： - **功能**：将数据层的输出转换为图结构（邻接矩阵和节点特征矩阵），便于GNN处理。这包括图的嵌入和初始化。 - **处理过程**： - 定义节点（如仓库、配送中心）和边（路径）。 - 构建邻接矩阵 $A$（表示连接关系）和特征矩阵 $Z^{(0)}$（节点初始特征，如位置坐标）。 - 公式表示： $$ A = \begin{bmatrix} a_{11} & \cdots & a_{1n} \\ \vdots & \ddots & \vdots \\ a_{n1} & \cdots & a_{nn} \end{bmatrix}, \quad Z^{(0)} = [\mathbf{z}_1, \mathbf{z}_2, \dots, \mathbf{z}_n]^T $$ 其中 $a_{ij}$ 表示节点 $i$ 到 $j$ 的连接权重（如距离或时间），$\mathbf{z}_i$ 是节点 $i$ 的特征向量。 - **输出**：图数据结构 $(A, Z^{(0)})$。 - **关键技术**：图嵌入技术，如引用[2]中DiffPool的图聚类方法，可实现分层表示[^2]。 3. **GNN模型层（核心计算层）**： - **功能**：应用GNN模型进行图学习，提取高阶关系特征，输出预测或优化结果（如最短路径、ETA）。 - **模型架构**： - 常见GNN变体：GCN（Graph Convolutional Network）或DiffPool（用于分层聚类）。 - 处理流程：输入图数据经过多层GNN，每层更新节点嵌入。例如，DiffPool层的输出： $$ (A^{(l+1)}, Z^{(l+1)}) = \text{DIFFPOOL}(A^{(l)}, Z^{(l)}) $$ 其中 $l$ 表示层编号，输出更粗糙的图表示。 - 损失函数：针对物流任务设计，如路径优化使用强化学习（PPO算法），引用[3]提到顺丰科技应用PPO实现动态路由决策响应时间<3秒[^3]。 - **输出**：优化后的节点嵌入 $Z^{(L)}$ 或决策向量（如路径概率分布）。 - **关键技术**：结合强化学习（如GraphPPO）处理实时决策，引用[2]提到图强化学习方法[^2]。 4. **应用层（输出与集成层）**： - **功能**：将GNN输出转换为TMS可执行的决策，如路径规划、资源分配，并反馈到业务系统。 - **处理过程**： - 决策模块：生成优化路线或调度计划。 - 集成接口：嵌入到TMS软件（如实时监控系统）。 - 性能指标：响应时间（引用[3]中目标<3秒）、准确性（如F1-score）。 - **输出**：优化决策（如车辆调度方案）、可视化报告。 - **关键技术**：AI应用架构师角色确保技术落地，覆盖“模型→应用”链路[^1]。 #### 框架图总结（伪代码表示） 以下是框架的伪代码表示，模拟系统流程： ```python # TMS-GNN算法模型系统框架（伪代码） def tms_gnn_system(): # 1. 数据层 raw_data = load_data("orders,sensors") # 从数据库或IoT加载 X, W = preprocess(raw_data) # 特征提取和归一化 # 2. 图处理层 A = build_adjacency_matrix(W) # 构建邻接矩阵 Z0 = build_feature_matrix(X) # 构建节点特征矩阵 # 3. GNN模型层 model = GCN() or DiffPool() # 选择GNN模型，如DiffPool[^2] Z_optimized = model.train(A, Z0) # 训练输出优化嵌入 # 4. 应用层 decisions = apply_to_tms(Z_optimized) # 生成路径决策，集成到TMS return decisions # 输出优化结果，如动态路由 ``` 此框架强调端到端处理，AI架构师需平衡模型复杂性与实时性[^1]。在物流企业中，该框架可应用于路线预测或资源调度试点场景。 #### 注意事项 - **可靠性与来源**：此框架基于通用智能物流架构推导，结合了引用[1]的全链路理念和引用[2]的GNN技术。实际实现可能因企业需求而异（如使用PyTorch Geometric框架）。 - **缺失细节**：引用中未直接提供“TMS-GNN”的具体框架图，但引用[3]提到路径优化模型（如Neural Rewriting），可作为参考；如果您需要可视化图表，建议查阅《图神经网络实战》书籍或PyTorch Geometric文档[^1]。
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值