李沐动手学深度学习V2-双向循环神经网络Bidirectional RNN和代码实现

一. 双向循环神经网络和代码实现

1. 介绍

在序列学习中，以往假设的目标是：在给定观测的情况下（例如在时间序列的上下文中或在语言模型的上下文中），对下一个输出进行建模，虽然这是一个典型情景，但不是唯一的，例如我们考虑以下三个在文本序列中填空的任务：

• 我___。
• 我___饿了。
• 我___饿了，我可以吃半头猪。

根据可获得的信息量，我们可以用不同的词填空，如“很高兴”（“happy”）、“不”（“not”）和“非常”（“very”）。很明显每个短语的“下文”传达了重要信息（如果有的话），而这些信息关乎到选择哪个词来填空，所以无法利用这一点的序列模型将在相关任务上表现不佳。
例如如果要做好命名实体识别（例如，识别“Green”指的是“格林先生”还是绿色），不同长度的上下文范围重要性是相同的。

2. 双向模型

在前向模式下“从第一个词元开始运行”的循环神经网络，同时需要增加一个“从最后一个词元开始从后向前运行”的双向循环神经网络，下图所示描述了具有单个隐藏层的双向循环神经网络的架构。

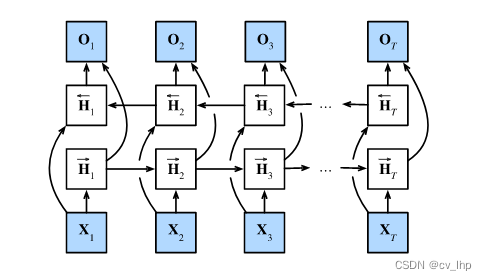
3. 定义

对于任意时间步$t$，给定一个小批量的输入数据${\mathbf{X}}_t\in {\mathbb{R}}^{n\times d}$（样本数：$n$，每个示例中的输入数：$d$），并且令隐藏层激活函数为$\varphi$。在双向架构中，我们设该时间步的前向和反向隐状态分别为${\overrightarrow{\mathbf{H}}}_t\in {\mathbb{R}}^{n\times h}$和${\overleftarrow{\mathbf{H}}}_t\in {\mathbb{R}}^{n\times h}$，其中$h$是隐藏单元的数目。前向和反向隐状态的更新如下：
H → t = ϕ ( X t W x h ( f ) + H → t − 1 W h h ( f ) + b h ( f ) ) , H ← t = ϕ ( X t W x h ( b ) + H ← t + 1 W h h ( b ) + b h ( b ) ) , \begin{aligned} \overrightarrow{\mathbf{H}}_t &= \phi(\mathbf{X}_t \mathbf{W}_{xh}^{(f)} + \overrightarrow{\mathbf{H}}_{t-1} \mathbf{W}_{hh}^{(f)} + \mathbf{b}_h^{(f)}),\\ \overleftarrow{\mathbf{H}}_t &= \phi(\mathbf{X}_t \mathbf{W}_{xh}^{(b)} + \overleftarrow{\mathbf{H}}_{t+1} \mathbf{W}_{hh}^{(b)} + \mathbf{b}_h^{(b)}), \end{aligned} H t​H t​​