小白懂的动态规划

1. 动态规划之01背包

1.1. 纯01背包问题

问题描述

  有N件物品和一个最多能背重量为W的背包，第i件物品的重量为weight[i]，得到的价值是value[i]。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。
  例如，三个物品：weight : {1,3,4}，value: {15,20,30}；背包容量：bagweight : 4

思路

代码

func totalValue(bagWeight int, weight []int, value []int ) int {
	dp := make([]int, bagWeight + 1)
	for i := 0; i < len(weight); i++ {
		for j := bagWeight; j >= weight[i]; j-- {
			dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
		}
	}
	return dp[bagWeight]
}

func max(a, b int) int {
	if a < b {
		a = b
	}
	return a
}


func main () {
	sc := bufio.NewScanner(os.Stdin)
	sc.Scan()
	bagWeight, _ := strconv.Atoi(sc.Text())

	sc.Scan()
	l1 := strings.Split(sc.Text(), ",")
	weight := make([]int, len(l1))
	for i := 0; i < len(l1); i++ {
		v, _ := strconv.Atoi(l1[i])
		weight[i] = v
	}

	sc.Scan()
	l2 := strings.Split(sc.Text(), ",")
	value := make([]int, len(l2))
	for i := 0; i < len(l2); i++ {
		v, _ := strconv.Atoi(l2[i])
		value[i] = v
	}

	fmt.Println(totalValue(bagWeight, weight, value))
}

1.2. LeetCode 494 目标和

问题描述

思路

1. 将求目标和的问题，转换为背包问题
2. 解背包问题

代码

	func findTargetSumWays(nums []int, target int) int {
	    var sum int
	    for i := 0; i < len(nums); i++ {
	        sum += nums[i]
	    }
	    if target > sum {
	        return 0
	    }
	    if ( sum + target ) % 2 == 1 {
	        return 0
	    }
	    
	    bagWeight := ( sum + target ) / 2
	    dp := make([]int, bagWeight + 1)
	    dp[0] = 1
	
	    for i := 0; i < len(nums); i++ {
	        for j := bagWeight; j >= nums[i]; j-- {
	            dp[j] += dp[j - nums[i]]
	        }
	    }
	    return dp[bagWeight]
	}

1.3. LeetCode474. 一和零

问题描述

给你一个二进制字符串数组 strs 和两个整数 m 和 n 。

请你找出并返回 strs 的最大子集的大小，该子集中 最多 有 m 个 0 和 n 个 1 。

如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的 子集 。

思路

1. 将问题转换为背包问题
2. 构造背包weight数组
3. 从2个维度遍历背包

代码

func findMaxForm(strs []string, m int, n int) int {
    var weight0 []int = make([]int, len(strs))
    var weight1 []int = make([]int, len(strs))
    
    dp := make([][]int, m + 1)
    for i := 0; i < m + 1; i++ {
        dp[i] = make([]int, n + 1)
    }

    for i := 0; i < len(strs); i++ {
        for j := 0; j < len(strs[i]); j++ {
            if strs[i][j] == '0' {
                weight0[i]++
            } else {
                weight1[i]++
            }
        }
    }

    for i := 0; i < len(strs); i++ {
        for j := m; j >= weight0[i]; j-- {
            for k := n; k >= weight1[i]; k-- {
                dp[j][k] = max(dp[j][k], dp[j - weight0[i]][k - weight1[i]] + 1)
            }
        }
    }
    return dp[m][n]
}

func max(a, b int) int {
    if a < b {
        a = b
    }
    return a
}

2. 动态规划之完全背包

  有N件物品和一个最多能背重量为W的背包，第i件物品的重量为weight[i]，得到的价值是value[i]。每种物品在背包中可以放多个，求解将哪些物品装入背包里物品价值总和最大。

  01背包要求，每种物品在背包中只能用一次。完全背包和01背包不同的一点在于，每种物品在背包中可以有无限件。

  例如，三个物品：weight : {1,3,4}，value: {15,20,30}；背包容量：bagweight : 4

2.1. 纯完全背包问题

问题描述

  有N件物品和一个最多能背重量为W的背包，第i件物品的重量为weight[i]，得到的价值是value[i]。每种物品在背包中可以放多个，求解将哪些物品装入背包里物品价值总和最大。

思路

1. 遍历物体
2. 遍历背包

代码

/**
    @author: HYK
    @date: 2021/6/17
    @email: flyingmonkey_hyk@163.com
    @note: Think Twice, Code Once!
**/
package main

import (
	"bufio"
	"fmt"
	"os"
	"strconv"
	"strings"
)

func allBag(bagWeight int, weight []int, value []int ) int {
	dp := make([]int, bagWeight + 1)
	for i := 0; i < len(weight); i++ {
		for j := weight[i]; j <= bagWeight; j++ {
			dp[j] = mmax(dp[j], dp[j - weight[i]] + value[i])
		}
	}
	return dp[bagWeight]
}

func mmax(a, b int) int {
	if a < b {
		a = b
	}
	return a
}
func main () {
	sc := bufio.NewScanner(os.Stdin)
	sc.Scan()
	bagWeight, _ := strconv.Atoi(sc.Text())

	sc.Scan()
	l1 := strings.Split(sc.Text(), ",")
	weight := make([]int, len(l1))
	for i := 0; i < len(l1); i++ {
		v, _ := strconv.Atoi(l1[i])
		weight[i] = v
	}

	sc.Scan()
	l2 := strings.Split(sc.Text(), ",")
	value := make([]int, len(l2))
	for i := 0; i < len(l2); i++ {
		v, _ := strconv.Atoi(l2[i])
		value[i] = v
	}

	fmt.Println(allBag(bagWeight, weight, value))
}

2.2. Leetcode 518 零钱兑换II

问题描述

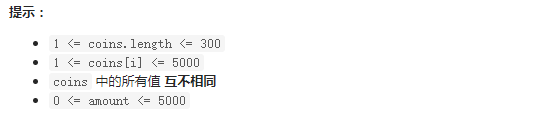
给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。

请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。

假设每一种面额的硬币有无限个。

题目数据保证结果符合 32 位带符号整数。

思路

完全背包

代码

func change(amount int, coins []int) int {
    dp := make([]int, amount + 1)
    dp[0] = 1

    for i := 0; i < len(coins); i++ {
        for j := coins[i]; j <= amount; j++ {
            dp[j] += dp[j - coins[i]]
        }
    }
    return dp[amount]
}