PCA主成分分析 实验

目录

1.PCA主成分分析

1.1 概述

2.算法原理，步骤

2.1 原理

2.2 步骤

3.案例

3.1 代码实现

3.2 运行结果

3.3 总结

---

1.PCA主成分分析

1.1 概述

       PCA（principal components analysis）即主成分分析技术，又称主分量分析，旨在利用降维的思想，把多指标转化为少数几个综合指标。

       在统计学中，主成分分析PCA是一种简化数据集的技术。它是一个线性变换。这个变换把数据变换到一个新的坐标系统中，使得任何数据投影的第一大方差在第一个坐标上，第二大方差在第二个坐标上，依次类推。主成分分析经常用于减少数据集的维数，同时保持数据集的对方差贡献最大的特征。这是通过保留低阶主成分，忽略高阶主成分做到的。

2.算法原理，步骤

2.1 原理

PCA的主要思想是将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征。

2.2 步骤

主成分的计算步骤如下：

1.对所有样本进行中心化：

2.计算样本的协方差矩阵

3.计算特征值与特征向量

解特征方程求出特征值，并使其按大小顺序排列。

分别求出对应于特征值的特征向量ei，要求||ei||=1

计算主成分贡献率及累计贡献率

4.计算主成分值

z=(Xe1,Xe2,...,Xei)

3.案例

3.1 代码实现

导入库

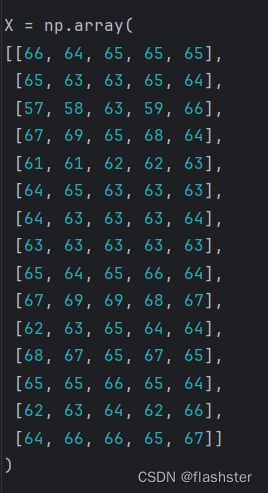
输入特征向量

n_components 指明了降到几维

利用数据训练模型（即上述得出特征向量的过程）

得出原始数据的降维后的结果；也可以以新的数据作为参数，得到降维结果。

打印各主成分的方差占比

3.2 运行结果

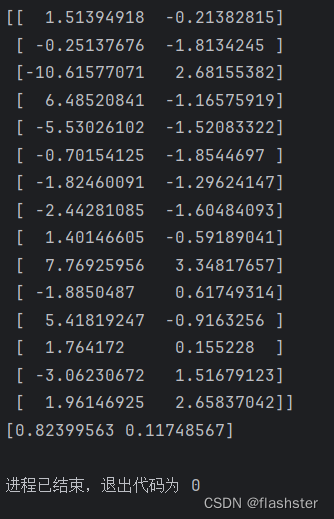
3.3 总结

优缺点

优点：

1.可以减少数据集的维数，有助于数据压缩和传输。

2.可以用于降维，使得数据更易于可视化。

3.可以作为一种去噪声方法，通过保留主成分来去除数据中的随机噪声。

缺点：

1.可能丢失信息：PCA通过减少维数来丢失一些信息，这些信息可能对于后续分析或决策很重要。

2.不适用于非高斯分布：PCA对数据分布假设较为敏感，如果数据不服从高斯分布，可能需要先进行转换。

3.不稳定性：PCA的结果对初始矩阵的排列顺序敏感，计算过程可能受到数据点排列的影响。