逻辑回归 实验

1.逻辑回归

1.1 概述

logistic回归又称logistic回归分析，是一种广义的线性回归分析模型，常用于数据挖掘，疾病自动诊断，经济预测等领域。 逻辑回归根据给定的自变量数据集来估计事件的发生概率，由于结果是一个概率，因此因变量的范围在 0 和 1 之间。 例如，探讨引发疾病的危险因素，并根据危险因素预测疾病发生的概率等。

2.算法原理，步骤

2.1 原理

初步思路：找一个线性模型来由X预测Y

z=x+b

但是很明显，这样的函数图像是类似一条斜线，难以达到0或1的取值

引入Sigmoid函数（逻辑函数）

g(x)=

2.2 图像

2.3 步骤

1.寻找一个合适的预测函数,一般是h函数。这个函数就是我们要找分类函数，用来预测输入数据的判断结果。这个过程很重要，需要对数据有一定的了解和分析，知道或猜测函数大概的形式，比如说是线性函数还是非线性函数。

2.构造一个Cost函数(即损失函数)，该函数用来表示预测函数（h）与训练数据类别（y）之间的偏差。

3.想办法使得J ( θ )最小并且求得最佳参数。J ( θ ) 函数的值越小，表示预测函数越准确，所以要找到J （ θ ）函数的最小值。找函数的最小值有不同的方法，这里使用的是梯度下降法。

3.案例

3.1 代码实现

导入python库

sklearn.datasets:导入数据集

train_test_split:划分训练集和测试集

定义随机种子

通过设定随机数种子，使运行得到的随机结果相同。

使实验结果更加准确

定义sigmoid函数

g(x)=

定义逻辑回归算法，

初始化参数w，b

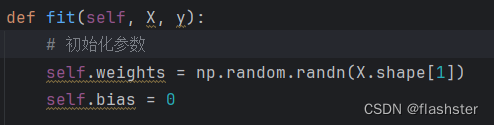
y=b+w1x1+w2x2+....+wnxn

定义权重w与偏置b

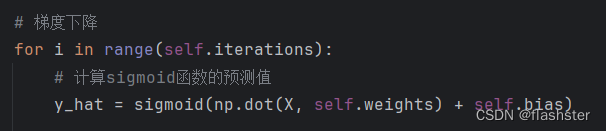
将y=w*x+b代入sigmoid函数

损失函数

为了衡量预测值与真实值之间的差异，定义损失函数使预测值更加接近真实值

计算梯度

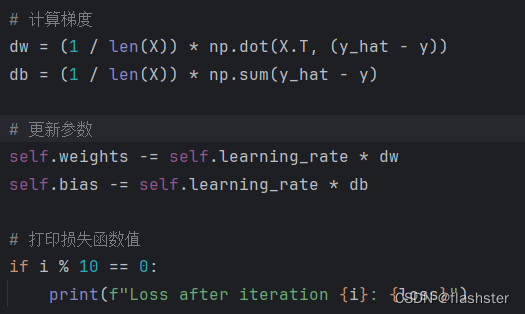
用梯度下降法更新参数，使代价函数最小化

定义预测

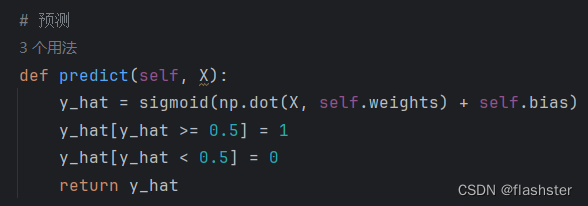
为了方便分类，将大于0.5的归为类别1，小于0.5的归为类别0

定义精度

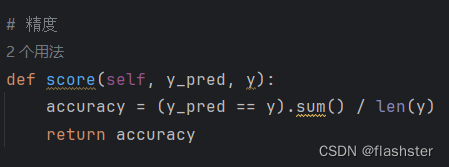
将分类正确的样本除以总样本，得到正确率

导入数据

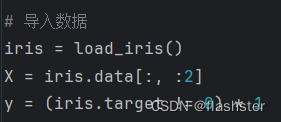
划分训练集和测试集

训练模型

输入学习率和迭代次数，然后调用fit

打印结果

将结果可视化

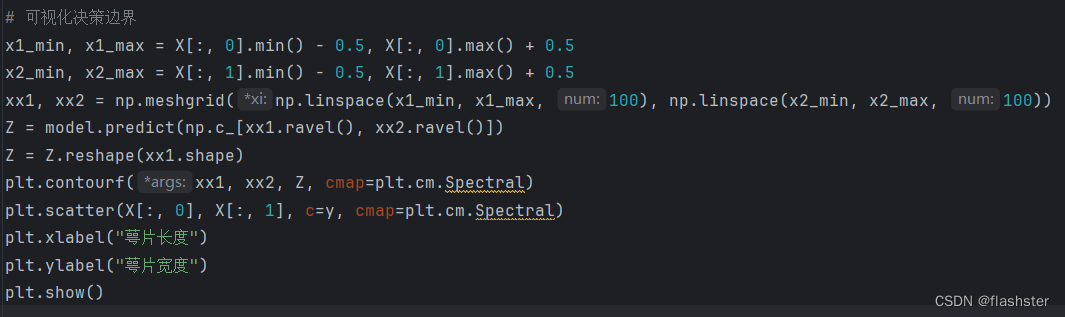
结果

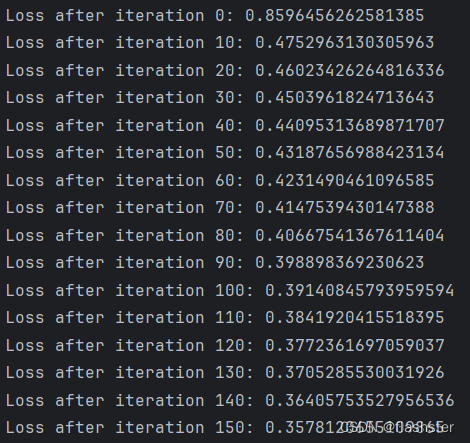
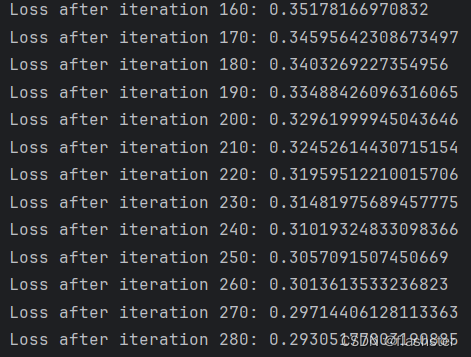
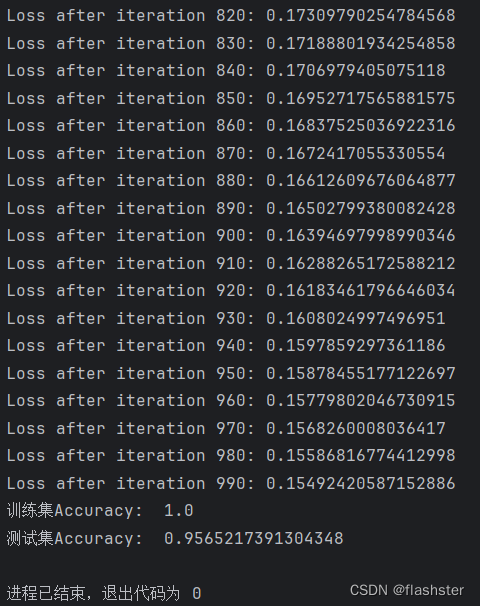
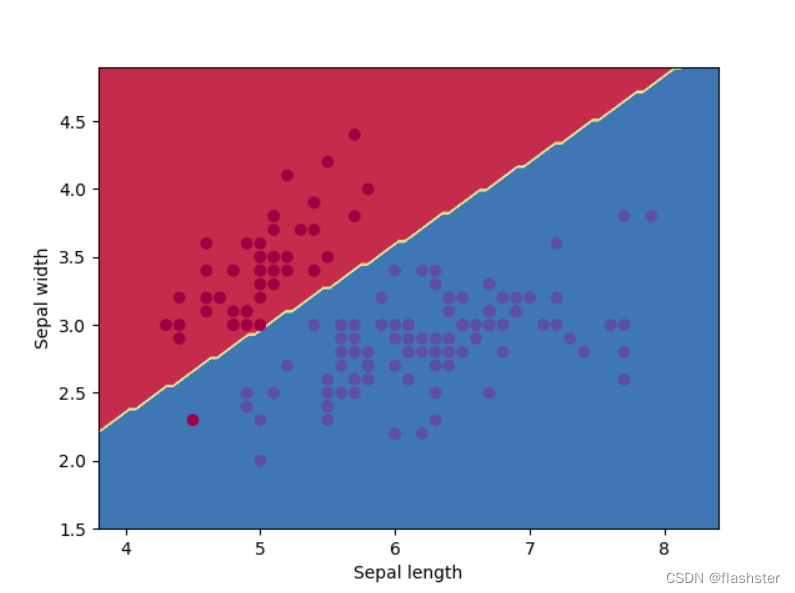
3.2 总结

优缺点

1、优点

（1）适合分类场景

（2）计算代价不高，容易理解实现。

（3）不用事先假设数据分布，这样避免了假设分布不准确所带来的问题。

（4）不仅预测出类别，还可以得到近似概率预测。

（5）目标函数任意阶可导。

2、缺点

（1）容易欠拟合，分类精度不高。

（2）数据特征有缺失或者特征空间很大时表现效果并不好。