支持向量机 实验

目录

1.支持向量机

1.1 概述

2.算法原理，步骤

2.1 公式

2.2 优化目标转换

2.3 步骤

3.案例

3.1 代码实现

3.2 运行结果

3.3 总结

---

1.支持向量机

1.1 概述

     支持向量机（Support Vector Machine, SVM）是一类按监督学习方式对数据进行二元分类的广义线性分类器，其决策边界是对学习样本求解的最大边距超平面。

     SVM使用铰链损失函数计算经验风险并在求解系统中加入了正则化项以优化结构风险，是一个具有稀疏性和稳健性的分类器 。SVM可以通过核方法进行非线性分类，是常见的核学习方法之一 。

2.算法原理，步骤

2.1 公式

线性分类

分隔超平面

f(x)=x+b

w是权重，b是截距

假设超平面将样本正确划分
       f(x) ≥ 1，y = +1
　　f(x) ≤ −1，y = −1

　　间隔：r=

2.2 优化目标转换

2.3 步骤

SVM算法可以分为以下几个步骤：

数据预处理：将数据集划分为训练集和测试集，并进行特征缩放（对数据进行标准化）。

构建模型：选择合适的核函数和惩罚系数，构建SVM模型。

训练模型：使用训练集对模型进行训练，通过最大化间隔来找到最优的超平面。

预测：使用训练好的模型对测试集进行预测。

3.案例

3.1 代码实现

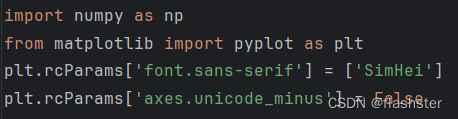
导入python库

定义随机种子

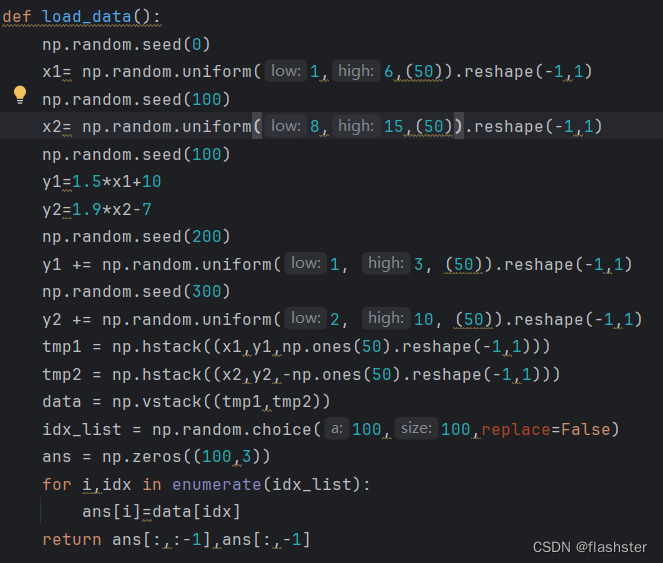
通过设定随机数种子，使运行得到的随机结果相同。

使实验结果更加准确

定义训练方式

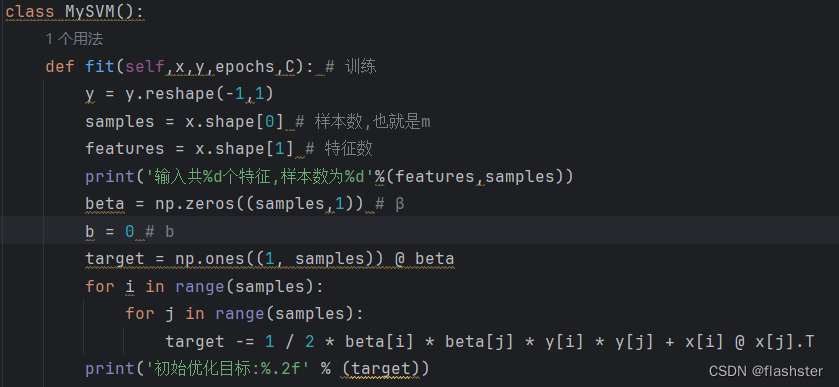
将导入的训练集进行分析，定义样本数与特征数

计算β的优化函数

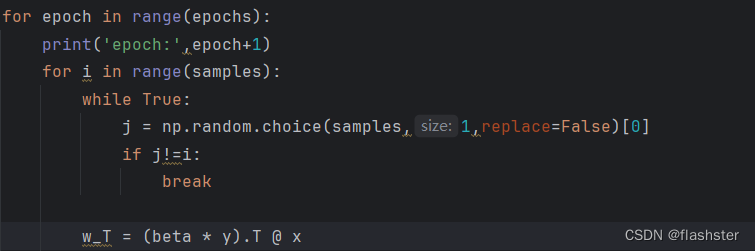
每次选取i和另一个数j作为更新数对
# 随机选择两个要更新的
w^T=∑βyx=(βyx)

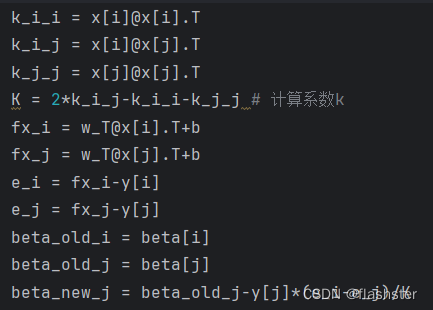
计算β_j^{new},把公式的2对应j,i对应1

裁剪beta_new_j

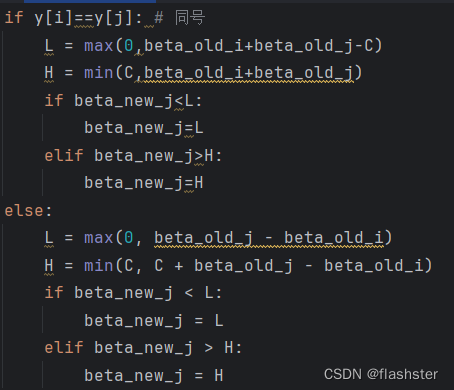
因为β_1^{old}y_1+β_2^{old}y_2=β_1^{new}y_1+β_2^{new}y_2=γ => β_1^{new}=y_1(γ-β_2^{new}y_2)
可以基于此解出beta_new_i,因为上面的裁剪,可以保证下面解出来的一定在[0,C]之间

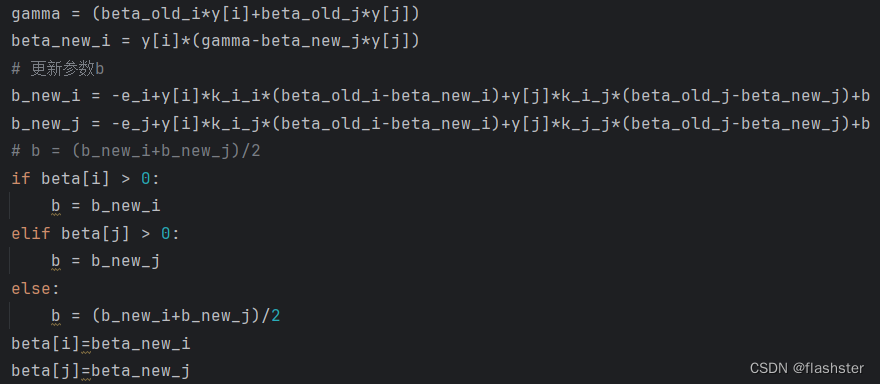
计算优化目标

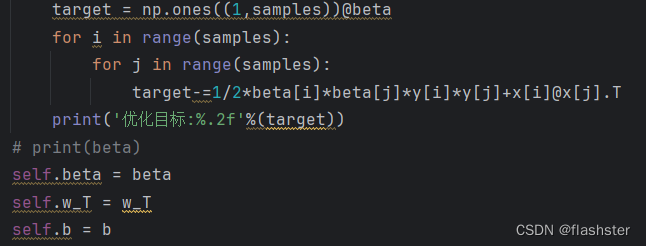
定义预测函数

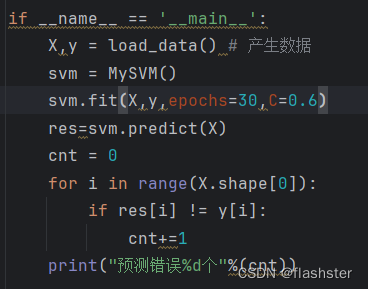
输入数据

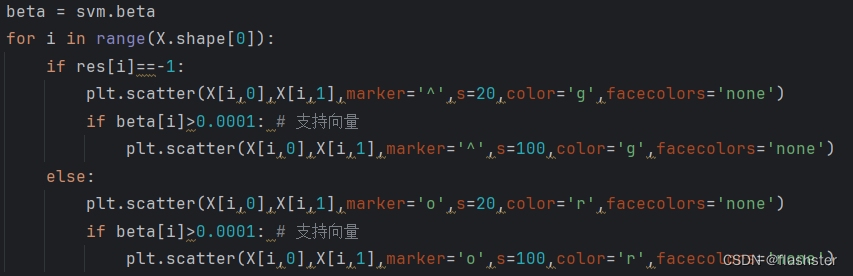
对每个数据点绘制,标出特殊点

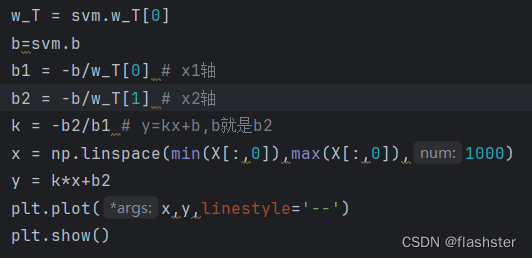
变量定义

3.2 运行结果

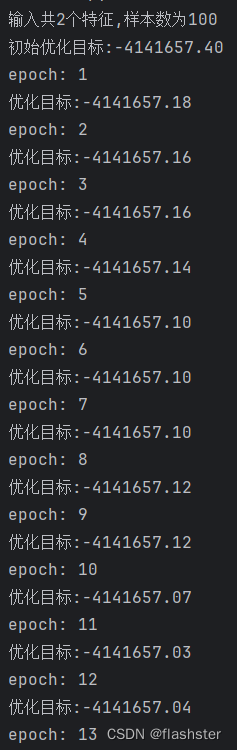
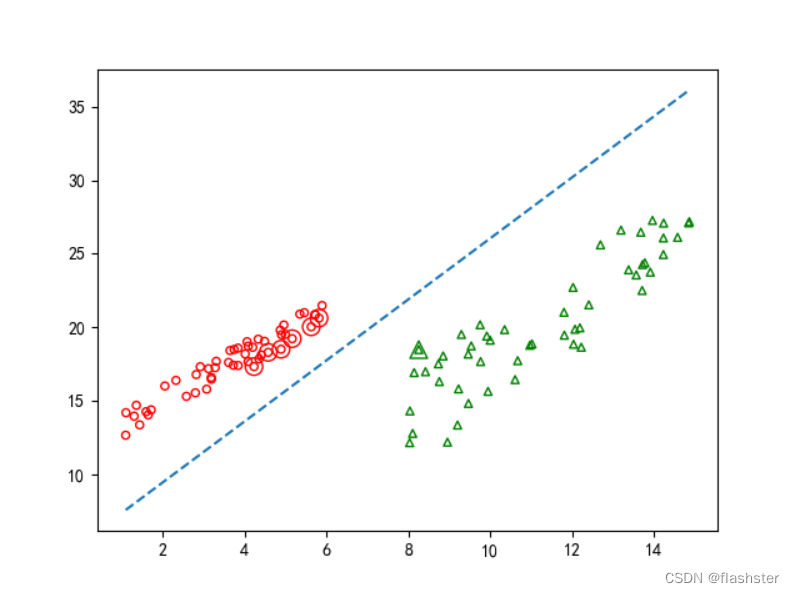
分析：

上图为支持向量机svm的决策面的分布的情况，从最终的决策面的位置可以看到，平面被分成两个区域，红圆圈、绿三角形分别为两类别的样本的分布情况，可以看到决策面对这些样本的划分情况还是能够区分开来不同类别的。

3.3 总结

优势：

1、适用性广泛

2、可避免陷入局部最优解，具有较低的泛化误差

3、高维空间有效

4、可控制的过拟合

劣势：

1、计算复杂度高，训练时间较长

2、参数选择敏感

3、对缺失数据敏感，选择合适的参数可能会比较困难

4、适用于二分类问题，对于多类别问题需要进行扩展或使用其他方法