CF 954C Matrix Walk

题目

There is a matrix A of size $x \times y$ filled with integers. For every , $A_{i, j} = y(i - 1) + j$. Obviously, every integer from $[1..xy]$ occurs exactly once in this matrix.

You have traversed some path in this matrix. Your path can be described as a sequence of visited cells $a_1, a_2, ..., a_n$ denoting that you started in the cell containing the number $a_1$, then moved to the cell with the number $a_2$, and so on.

From the cell located in $i$-th line and $j$-th column (we denote this cell as $(i, j)$) you can move into one of the following cells:

1. $(i + 1, j)$ — only if $i < x$;
2. $(i, j + 1)$ — only if $j < y$;
3. $(i - 1, j)$ — only if $i > 1$;
4. $(i, j - 1)$ — only if $j > 1$.

Notice that making a move requires you to go to an adjacent cell. It is not allowed to stay in the same cell. You don’t know x and y exactly, but you have to find any possible values for these numbers such that you could start in the cell containing the integer $a_1$, then move to the cell containing $a_2$ (in one step), then move to the cell containing $a_3$ (also in one step) and so on. Can you choose $x$ and $y$ so that they don’t contradict with your sequence of moves?

Input
The first line contains one integer number $n$ $(1 \le n \le 200000)$ — the number of cells you visited on your path (if some cell is visited twice, then it’s listed twice).

The second line contains n integers $a_1, a_2, ..., a_n$ $(1 \le a_i \le 10^9)$ — the integers in the cells on your path.

Output
If all possible values of x and y such that $1 \le x, y \le 10^9$ contradict with the information about your path, print NO.

Otherwise, print YES in the first line, and in the second line print the values x and y such that your path was possible with such number of lines and columns in the matrix. Remember that they must be positive integers not exceeding $10^9$.

Examples

Input
8 1 2 3 6 9 8 5 2
Output
YES 3 3

Input
6 1 2 1 2 5 3
Output
NO

Input
2 1 10
Output
YES 4 9

Note
The matrix and the path on it in the first test looks like this:

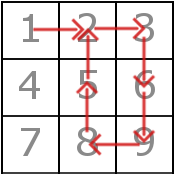
Also there exist multiple correct answers for both the first and the third examples.

分析

【题意】
给一个只含1~n的路径，选择长宽按照1~n顺序排列的方式生成一个地图，使得路径合法。

【分析】

• 对于一个图而言，宽度$w$定了以后，所有的点的位置就确定了，而长度只影响取值的范围。所以我们不关心长度，只关心宽度$w$。
• 在一个宽度为$w$的图上移动，上下走的跨度也是$w$，而左右走的跨度永远是$1$，所以对于合法的路径而言，相邻的两个点的差不是$1$，就是$w$。所以我们只关心它的跨度$w$。

判断某条路径合法，首先应该满足上面第二条基本性质，才有可能找到一个地图吧——一旦某两个点的差是一个大于$1$的数，说明它向上/下走了，也就间接限制了地图的宽度只能是这么多，那么反过来，地图的宽度也限制了向上/下走的跨度只能是这么多。所以一个合法路径只能有一个跨度。

在路径的跨度也就是地图的$w$确定以后，再检查是否合法就容易多了，只需根据每个位置计算出向上下左右行走的可能，并判度下一个位置是否是可能性中的一种就行了。

【注意】
如果两个点是上下关系，它们相差$w$就一定相邻，反之就一定不相邻，相差$w$是一个很强的条件。
如果两个点是左右关系，它们相差并不能决定是否相邻，需要对它们的行列关系进行具体判断。

与其对两个点做很多的判断，我觉得不如把从一个点出发会到达的四种可能算出来，然后看其中有没有路径上的下一个点。

代码

#include<stdio.h>
#define max(a,b) ((a)>(b)?(a):(b))
#define min(a,b) ((a)<(b)?(a):(b))
#define mabs(x) ((x)>0?(x):(0-(x)))

#define N_max    200005
int arr[N_max];

int w=1;
int next[4];//0~3代表向上下左右行走会到哪里，-1表示不能走
void cal(int v, int w) {
    int x = v / w;
    int y = v%w;
    //上下好计算
    next[0] = ((v - w) > 0 ? v - w : -1);//考虑上边界
    next[1] = (v + w);
    next[2] = ((v - 1)>0 ? v - 1 : -1);//考虑左边界
    next[3] = v + 1;
    //左右需特判
    if (y== 0)
        next[3] = -1;
    else if (y == 1)
        next[2] = -1;
}
int main() {
    int n;
    scanf("%d", &n);
    for (int i = 0; i < n; i++) 
        scanf("%d", &arr[i]);
    for (int i = 1; i < n; ++i)
    {
        if (mabs(arr[i] - arr[i - 1]) > w) {
            if (w > 1) {
                printf("NO"); return 0;
            }
            w = mabs(arr[i] - arr[i - 1]);
        }   
    }
    int flag = 0;
    for (int i = 1; i < n; ++i) {
        flag = 0;
        cal(arr[i-1],w);
        for (int t = 0; t < 4; ++t)if (next[t] == arr[i])flag = 1;
        if (flag == 0) {
            printf("NO");
            return 0;
        }
    }
    printf("YES\n1000000000 %d",w);
}

总结

当直接判断两个点的关系是否正确很繁琐时，不妨考虑从一个点生成所有可能转移到的点，再检查这个集合是不是含有另一个点。