二叉树相关内容

1.二叉树的相关属性：

4.1二叉树的度（树的高度---层数）： 最大是2， 也就是一个节点的子节点的个数，0，1，2

     二叉树的深度： 

1）如果二叉树为空，结点的深度为0；

2）如果二叉树只有一个结点G为例，其中，它的左右子树的深度为0；而这种情况二叉树的深度为1。

3）如果二叉树有两个结点D，G为例，其中，以D为根结点的二叉树的左子树的深度为0，右子树的深度为（0+1）；而这种情况二叉树的深度为2。

4）如果二叉树有n个结点,二叉树的深度为二叉树左右子树深度的最大值+1。

4.2满二叉树： 二叉树只有度为 0 和 度为2 的结点，并且度为0 的结点在同一层上。

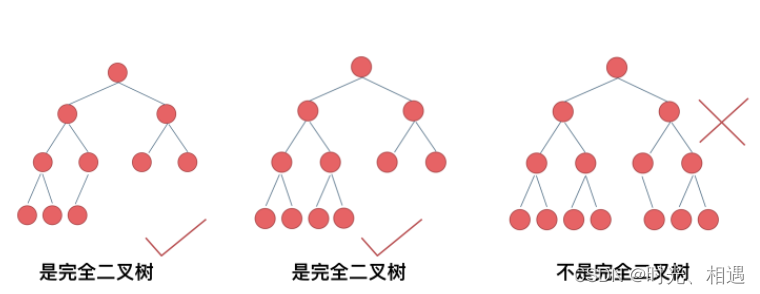
4.3完全二叉树：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^(h-1) 个节点。

什么是优先级队列呢？

其实就是一个披着队列外衣的堆，因为优先级队列对外接口只是从队头取元素，从队尾添加元素，再无其他取元素的方式，看起来就是一个队列。

而且优先级队列内部元素是自动依照元素的权值排列。那么它是如何有序排列的呢？

缺省情况下priority_queue利用max-heap（大顶堆）完成对元素的排序，这个大顶堆是以vector为表现形式的complete binary tree（完全二叉树）。

什么是堆呢？

堆是一棵完全二叉树，树中每个结点的值都不小于（或不大于）其左右孩子的值。 如果父亲结点是大于等于左右孩子就是大顶堆，小于等于左右孩子就是小顶堆。

所以大家经常说的大顶堆（堆头是最大元素），小顶堆（堆头是最小元素），如果懒得自己实现的话，就直接用priority_queue（优先级队列）就可以了，底层实现都是一样的，从小到大排就是小顶堆，从大到小排就是大顶堆。

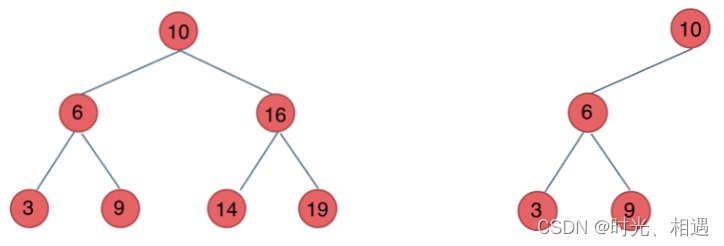
4.4二叉搜索树： 有序树

4.5    平衡二叉树：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

 4.6 二叉树可以链式存储---指针，也可以顺序存储---数组。

 4.7二叉树遍历方式：

• 深度优先遍历
  • 前序遍历（递归法，迭代法）
  • 中序遍历（递归法，迭代法）
  • 后序遍历（递归法，迭代法）
• 广度优先遍历
  • 层次遍历（迭代法）

2.链式存储的二叉树节点的定义方式

    //二叉树节点定义 的书写方式
    public class treeNode {
        int val;
        treeNode left;
        treeNode right;

        //无参构造
        public treeNode() {
        }

        //有参构造
        public treeNode(int val) {
            this.val = val;
        }

        //全参构造
        treeNode(int val, treeNode left, treeNode right) {
            this.val = val;
            this.left = left;
            this.right = right;
        }
    }

3.二叉树前中后序遍历(递归)

    //二叉树前序遍历
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        preorder(root,res);
        return res;
    }
    public void preorder(TreeNode root, List<Integer> res) {
        if (root == null) {
            return;
        }
        res.add(root.val);
        //遍历逻辑
        preorder(root.left,res);
        preorder(root.right,res);
    }

    //二叉树的中序遍历
     public List<Integer> inorderTraversal(TreeNode root){
        List<Integer> res = new ArrayList<>();
        inorder(root,res);
        return res;

     }
     public void inorder(TreeNode root, List<Integer> res){
        if (root == null) {
            return;
        }
        inorder(root.left,res);
        res.add(root.val);
        inorder(root.right,res);
     }

     //二叉树的后序遍历
    public List<Integer> postorderTraversal(TreeNode root){
        List<Integer> res = new ArrayList<>();
        postOrder(root,res);
        return res;

    }
    public void postOrder(TreeNode root, List<Integer> res){
        if (root == null) {
            return;
        }
        postOrder(root.left,res);
        postOrder(root.right,res);
        res.add(root.val);
    }

4.二叉树前中后序遍历(迭代)

详见代码随想录代码随想录

1.二叉搜索树，一般是进行中序遍历，因为中序遍历的结果，可以看作是有序数组，从小到大的顺序。

再加上 pre 节点和 cur(root)当前节点，进行中节点的逻辑处理；

2.取中间位置的元素，尽量不要 int mid = (left + right) / 2,因为如果left 和 right 都是Integer.MAX_VALUE的话，则会出现越界异常。因此 可以这样写：

int mid = left + (right - left) / 2;