【图论】图的最短路径问题——有权图的单源最短路(Dijkstra算法)

一、最短路径长度 

有权图的单源最短路与无权图的区别：

1.有权图的最短路不一定是经过顶点数最少的那条路

2.负值圈问题(negative-cost cycle)，不考虑

 

 

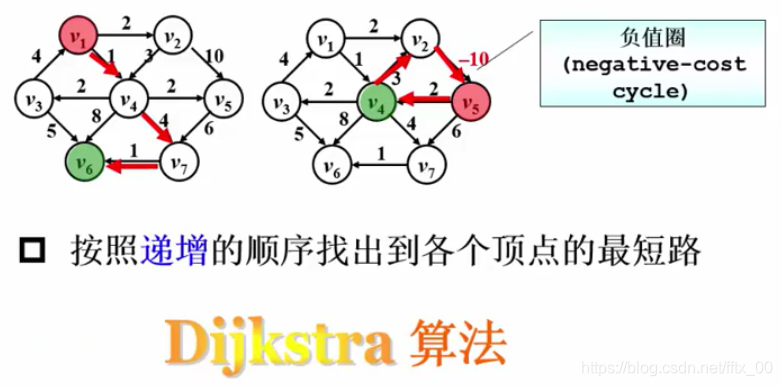
收录：

1.该点(在未被收录前)已经被所有已收录上层邻接点更新

2.该点的上层邻接点已经被全部收录

因此不会有更小的dist，即该点已解决。

初始化：

dist[S]=0，dis[其他]=∞（正无穷）；

path[所有]=-1；

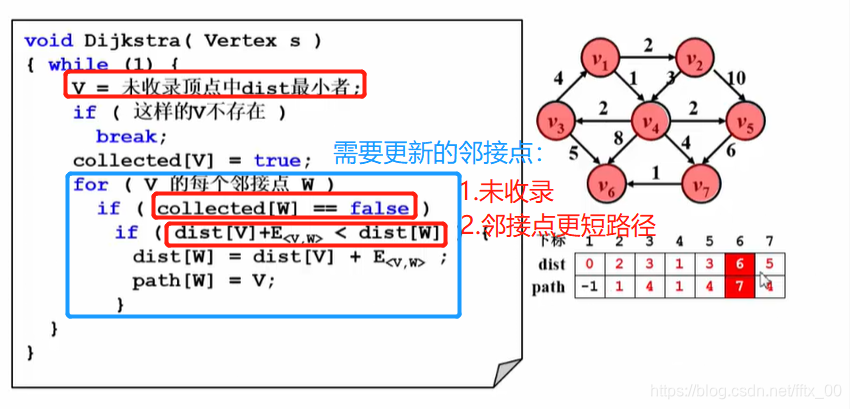
（不能解决有负边的情况）（实际上会循环n次，外层循环改成n的计数循环也一样的）

每次收录未收录顶点中dist最小者

保证了->收录V只可能使V邻接点的路径变短=min{dist[W],dist[V]+E<V,W>}

(反证法：如果收录V使非V邻接点K路径变短，

原先   dist[K]=E<S,W>+E<W,K>

收录后dist[K]=E<S,V>+E<V,K>

因为K邻接点W一定是被收录过的，且W比V先被收录；

因此E<S,W>一定小于等于E<S,V>；

收录V不会使非V邻接点路径变短)

BFS正好实现了无权图中每次收录顶点中dist最小者。

dist=0，1，2，3，4…

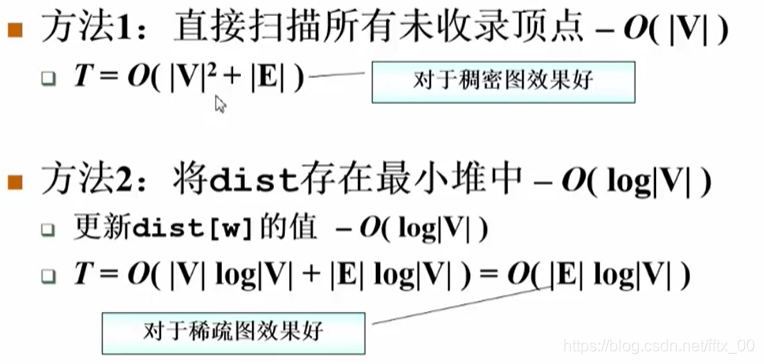
二、第二标尺

//1:新增边权
for(int j=0;j<N;j++){
        if(collected[j]==0 && G[minid][j]!=INFINITE){//未收录的邻接点
            if(dist[minid]+G[minid][j]<dist[j]){//若需要更新路径长度
                dist[j]=dist[minid]+G[minid][j];
                cost[j]=cost[minid]+P[minid][j];
            }else if(dist[minid]+G[minid][j]==dist[j]){//最短距离相同时，是否边权更小
                if(cost[minid]+P[minid][j]<cost[j]){
                    cost[j]=cost[minid]+P[minid][j];
                }
            }
        }
    }

//2：新增点权
for(int j=0;j<N;j++){
        if(collected[j]==0 && G[minid][j]!=INFINITE){//未收录的邻接点
            if(dist[minid]+G[minid][j]<dist[j]){//若需要更新路径长度
                dist[j]=dist[minid]+G[minid][j];
                w[j]=w[minid]+weight[j];
            }else if(dist[minid]+G[minid][j]==dist[j]){//最短距离相同时，是否点权更大
                if(w[minid]+weight[minid]>w[j]){
                    w[j]=w[minid]+weight[j];
                }
            }
        }
    }

//3：求最短路径条数
for(int j=0;j<N;j++){
        if(collected[j]==0 && G[minid][j]!=INFINITE){//未收录的邻接点
            if(dist[minid]+G[minid][j]<dist[j]){//若需要更新路径长度
                dist[j]=dist[minid]+G[minid][j];
                num[j]=num[minid];//前驱结点更新为新的唯一结点，num继承前驱结点
            }else if(dist[minid]+G[minid][j]==dist[j]){//最短距离相同时
                num[j]+=num[minid];//前驱结点增加了，num增加
            }
        }
    }

三、最短结点路径

1.记录单一最短路径，单一前驱结点pre[MAXN]

2.记录所有最短路径，所有前驱结点vector<int> pre[MAXN]

对每个结点，pre[i]是一个变长数组，存放点i的所有能产生最短路径的前驱结点

（或者设置为set<int> 数组,此时使用pre[v].count(u)来查询比较方便）

//1:找到所有最短路径

<1>pre数组不需要赋初值

<2>如果需要更新距离，dist[minid]+G[minid][i]<dist[i]；

此时需要先清空当前pre[i]数组，然后再添加minid作为其前驱结点

由于每次找到更优的前驱时都会清空pre[i]，因此pre数组不需要初始化 

//1:找到所有最短路径
vector<int> pre[MAXN];
    for(int i=0;i<N;i++){
        if(collected[i]==0 && G[minid][i]!=INFINITE){//未收录的邻接点
            if(dist[minid]+G[minid][i]<dist[i]){
                dist[i]=dist[minid]+G[minid][i];
                pre[i].clear();
                pre[i].push_back(minid);
            }else if(dist[minid]+G[minid][i]==dist[i]){
                pre[i].push_back(minid);
            }
        }
    }

//2:遍历所有最短路径，找到一条使第二标尺最优的路径

• 记录最短路径的数组Path
• 临时记录当前路径的数组tempPath
• 第二标尺最优值：optValue

 

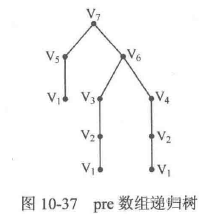
递归边界：到达叶子结点，即起点

将本次的临时路径tempPath的第二标尺值与最优值optValue比较

(更新optValue，使用tempPath覆盖Path)

递归式：如果当前访问结点v，遍历所有pre[v]进行递归

每次需要删除tempPath新增加的结点，

防止下一次添加结点进临时路径时，结点前面多出了一堆不属于当前路径的结点

最终Path数组中存放结果路径结点的逆序

四、Dijkstra算法程序示例

//邻接矩阵法
#include <iostream>
#define MAXN 510
#define MAXDATA 1000000000
using namespace std;

int G[MAXN][MAXN];
int nv,ne,c1,c2;

int dis[MAXN];
int collected[MAXN];
void Dijkstra1(){
    fill(dis,dis+nv,MAXDATA);
    dis[c1]=0;
    while(1){
        //1:FindMin
        int minValue=MAXDATA,minId=-1;
        for(int i=0;i<nv;i++){
            if(!collected[i] && dis[i]<minValue){//未收录中最小的
                minValue=dis[i];
                minId=i;
            }
        }
        if(minId==-1) return;
        collected[minId]=1;
        //2:main part
        for(int j=0;j<nv;j++){
            if(!collected[j] && G[minId][j]!=MAXDATA){
                if(dis[j]>dis[minId]+G[minId][j]){
                    dis[j]=dis[minId]+G[minId][j];
                }
            }
        }
    }
}

int main(){
    scanf("%d %d %d %d",&nv,&ne,&c1,&c2);

    for(int i=0;i<nv;i++){
        for(int j=0;j<nv;j++){
            G[i][j]=MAXDATA;
        }
    }

    int tmp1,tmp2,tmpl;
    for(int i=0;i<ne;i++){
        scanf("%d %d %d",&tmp1,&tmp2,&tmpl);
        G[tmp1][tmp2]=tmpl;
    }

    Dijkstra1();

    printf("%d",dis[c2]);

    return 0;
}

//邻接表法
#include <iostream>
#include <vector>
#include <queue>
#define MAXN 1010
#define INFINITY 100
using namespace std;

int Nv,Ne;
struct LNode
{
    int data;
    int weight;
    LNode* next;
};

LNode* G[MAXN];

void CreateL(){
    cin>>Nv>>Ne;

    int v1,v2,w;
    for(int i=0;i<Ne;i++){
        cin>>v1>>v2>>w;
        LNode* tmp=new LNode;
        tmp->data=v2;
        tmp->weight=w;
        tmp->next=G[v1];
        G[v1]=tmp;
    }
}


int FindMin(int* dist,int* collected){
//遍历找最小：适用于稠密图
    int MinDist=INFINITY;
    int MinV=-1;
    for(int i=0;i<Nv;i++){
        if(collected[i]==-1 && MinDist>dist[i]){
            MinDist=dist[i];
            MinV=i;
        }
    }

    return MinV;
}

void Dijkstra(int S,int* dist,int* path,int* collected){
    dist[S]=0;

    int vetex;
    while(1){
        vetex=FindMin(dist,collected);
        if(vetex==-1) break;
        collected[vetex]=1;

        LNode* w=G[vetex];
        while(w){
            if(collected[w->data]==-1){
                if(dist[vetex]+w->weight<dist[w->data]){
                    dist[w->data]=dist[vetex]+w->weight;
                    path[w->data]=vetex;
                }
            }
            w=w->next;
        }        
    }   
}

void PrintL(int vetex,int* path){
    cout<<vetex;
    
    int w=path[vetex];
    while(w!=-1){
        cout<<" "<<w;
        w=path[w];
    }
}


int main(){
    CreateL();

    int dist[MAXN],path[MAXN];
    int collected[MAXN];
//dist初始化为极大值
    fill(dist,dist+Nv,INFINITY);
    fill(path,path+Nv,-1);
//collected初始化为-1
    fill(collected,collected+Nv,-1);

    Dijkstra(0,dist,path,collected);
    PrintL(5,path);

    return 0;
}

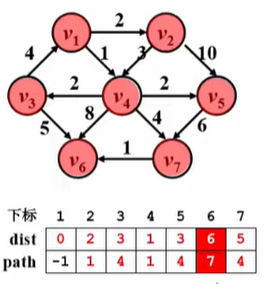
测试数据：

7 12
0 1 2
0 3 1
1 3 3
1 4 10
2 0 4
2 5 5
3 2 2
3 4 2
3 5 8
3 6 4
4 6 6
6 5 1