从线性到非线性，用混合模型破解数据的隐藏规律

原创

于 2025-09-21 13:36:19 发布 · 667 阅读

13 ·

CC 4.0 BY-SA版权

文章标签：

#python

一、引言

今天我们来讨论两个专门处理有分组或者重复测量的的数据的模型，分别为拟合线性趋势的线性混合模型，拟合非线性趋势的非线性混合模型。线性混合模型（LMM）和非线性混合模型（NLMM），它们既能捕捉数据的整体趋势，又能兼顾个体或分组差异。

二、模型原理

如下表，普通的回归模型和混合模型的核心差异是数据有无分组或者重复测量。

线性混合模型和非线性混合模型的混合体现在两个效应上，分别为固定效应：所有样本共有的趋势，随机效应：分组特有的差异。

如下图，观察五条竖线，可以发现整体成绩随时间上升，观察竖线不同颜色的点，可以发现不同班级间的成绩不同。

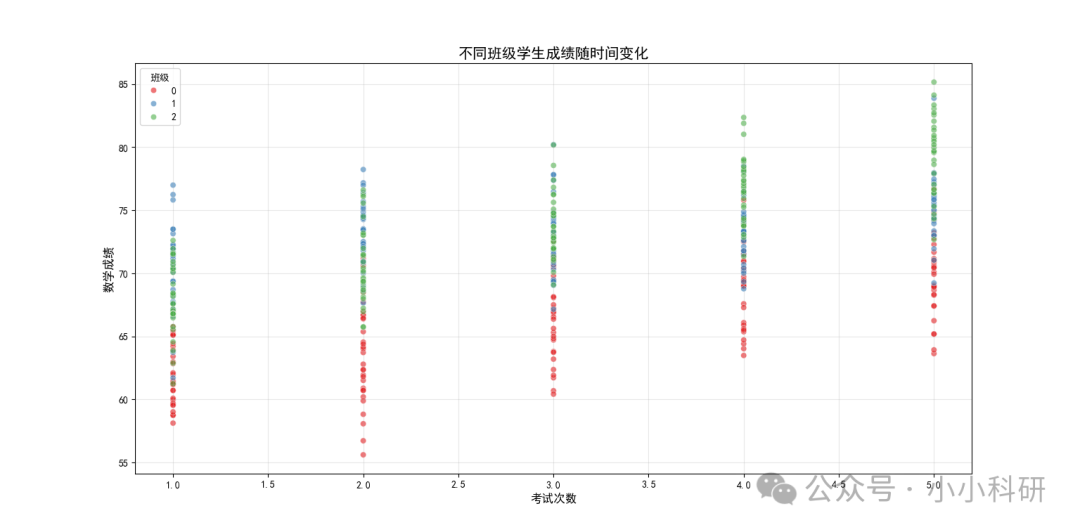
三、代码实操

我们以学生成绩为因变量，引入学习时长作为自变量，用3个不同班级的数据进行分别拟合线性混合模型和非线性混合模型。我们最后还会对比哪个模型拟合效果最好。（注意以下均为R软件代码）

01、数据准备

下面我们用模拟数据来搭建模型。

# 生成模拟数据并可视化
library(ggplot2)
set.seed(123)
# 设定参数：3个班级，5次测量
n_class <- 3
n_student <- 30
n_time <- 5
class_id <- rep(1:n_class, each = n_student*n_time)
student_id <- rep(1:(n_class*n_student), each = n_time)
time <- rep(1:n_time, n_class*n_student)
# 生成数据（带随机效应和非线性趋势）
base_score <- c(60, 70, 65)  # 班级基线差异
growth_rate <- c(2, 1.5, 3)  # 班级初始增长率
nonlinear_effect <- ifelse(class_id == 2, -0.1*(time^2), 0)  # 班级2的非线性衰减
random_error <- rnorm(n_class*n_student*n_time, 0, 3)
score <- base_score[class_id] + growth_rate[class_id]*time + nonlinear_effect + random_error
# 转换为数据框
data <- data.frame(
  班级 = factor(class_id),

最低0.47元/天解锁文章