别让高维数据 “困住” 你！主成分分析与因子分析实操指南

最新推荐文章于 2025-12-18 11:52:33 发布

原创最新推荐文章于 2025-12-18 11:52:33 发布 · 1.1k 阅读

19 ·

CC 4.0 BY-SA版权

文章标签：

#人工智能

一、引言

面对学生十几科成绩、产品二十多项检测指标这类高维数据，想抓规律却总被数据“淹没”？主成分分析（PCA）和因子分析这两个“数据工具”能帮上忙。今天不只是讲概念，更结合代码实操，带你实实在在学会用它们拆解复杂数据。

二、核心原理：两种分析的“底层逻辑”

先花2分钟搞懂原理，后面实操更清晰

主成分分析（PCA）本质是 “数据降维工具”，其数学原理基于协方差矩阵的特征分解。具体步骤如下：

1.设原始数据矩阵为

（n为样本数，p为变量数），先对X进行标准化处理。

2.计算协方差矩阵：

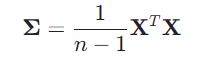
3.对协方差矩阵进行特征分解：

其中U是由特征向量组成的正交矩阵，Λ是包含特征值的对角矩阵。

4.按特征值大小排序后，选取前k个最大特征值对应的特征向量u1,u2,⋯,uk构成投影矩阵W=[u1,u2,⋯,uk]。

5.得到降维后的数据：

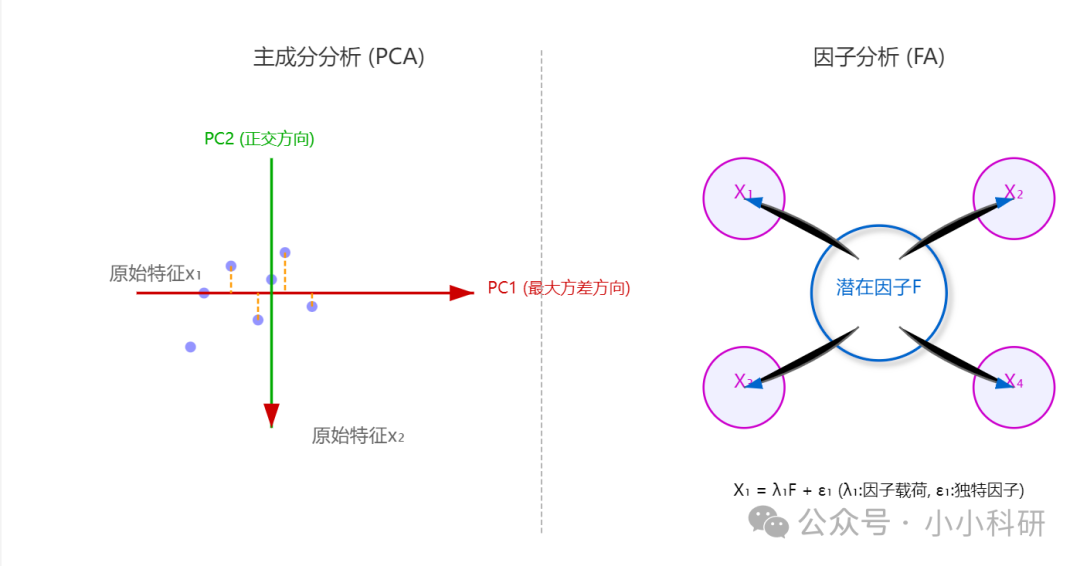
PCA 的核心在于通过最大化投影后数据的方差，实现 “丢冗余保关键”，例如将p个相关变量整合为k个不相关的 “主成分”。

因子分析更像 “潜在规律探测器”，其数学模型为：x=Λf+ϵ其中，x是可观测的p维变量向量，Λ为因子载荷矩阵，f是m维不可观测的潜在因子向量（m<p），ϵ是特殊因子向量，代表无法被潜在因子解释的部分。因子分析通过估计Λ和f，揭示变量间的相关性本质。

例如通过最大似然估计或主成分法求解，发现 “语文阅读”“作文写作” 成绩相关，是因为背后存在 “语言素养” 因子；“数学计算”“几何证明” 关联，可能受 “逻辑思维” 因子影响。这些潜在因子虽无法直接测量，但能有效解释变量间的复杂关系。

三、主成分分析实操

代码随机生成10名学生5个科目的成绩，分别为'语文', '数学', '英语', '物理', '历史'。

import numpy as np
import pandas as pd
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import seaborn as sns
# 设置中文显示
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题
# 步骤1：生成随机数据
np.random.seed(42)  # 固定随机种子，保证结果可复现
# 生成10行5列数据（10名学生，5科成绩）
scores = np.random.randint(60, 100, size=(10, 5))
# 转为DataFrame，添加列名
df = pd.DataFrame(scores, columns=['语文', '数学', '英语', '物理', '历史'])
print("学生成绩数据：")
print(df)
# 步骤2：用PCA降维分析
# 1. 数据标准化（PCA需消除量纲影响）
scaler = StandardScaler()
scaled_data = scaler.fit_transform(df)
# 2. 提取2个主成分
pca = PCA(n_components=2)
pca_result = pca.fit_transform(scaled_data)
# 3. 查看主成分对原始变量的权重（载荷）
pca_loadings = pd.DataFrame(
    pca.components_,
    columns=df.columns,
    index=['主成分1', '主成分2']
)
print("\n主成分载荷（权重）：")
print(pca_loadings.round(2))
# 4. 查看各主成分解释的信息占比
print("\n主成分解释方差占比：")
print(pca.explained_variance_ratio_.round(2))
# 步骤3：可视化分析结果
# 1. 主成分得分散点图
pca_df = pd.DataFrame(pca_result, columns=['主成分1', '主成分2'])
pca_df['学生编号'] = [f'学生{i+1}' for i in range(10)]
plt.figure(figsize=(8, 6))
sns.scatterplot(
    data=pca_df,
    x='主成分1',
    y='主成分2',
    s=100,  # 点的大小
    color='skyblue',
    edgecolor='black'
)
# 添加学生编号标签
for i in range(10):
    plt.text(
        pca_df['主成分1'][i],
        pca_df['主成分2'][i],
        pca_df['学生编号'][i],
        fontsize=10,
        ha='right'
    )
plt.title('学生主成分得分散点图', fontsize=15)
plt.grid(alpha=0.3)
plt.show()
# 2. 主成分载荷热力图
plt.figure(figsize=(8, 4))
sns.heatmap(pca_loadings, annot=True, cmap='coolwarm', center=0)
plt.title('主成分载荷热力图', fontsize=15)
plt.show()
# 3. 方差解释率柱状图
plt.figure(figsize=(6, 4))
sns.barplot(
    x=['主成分1', '主成分2'],
    y=pca.explained_variance_ratio_,
    palette='pastel'
)
plt.ylim(0, 1)
plt.ylabel('解释方差占比')
plt.title('主成分方差解释率', fontsize=15)
for i, v in enumerate(pca.explained_variance_ratio_):
    plt.text(i, v+0.02, f'{v:.2f}', ha='center')
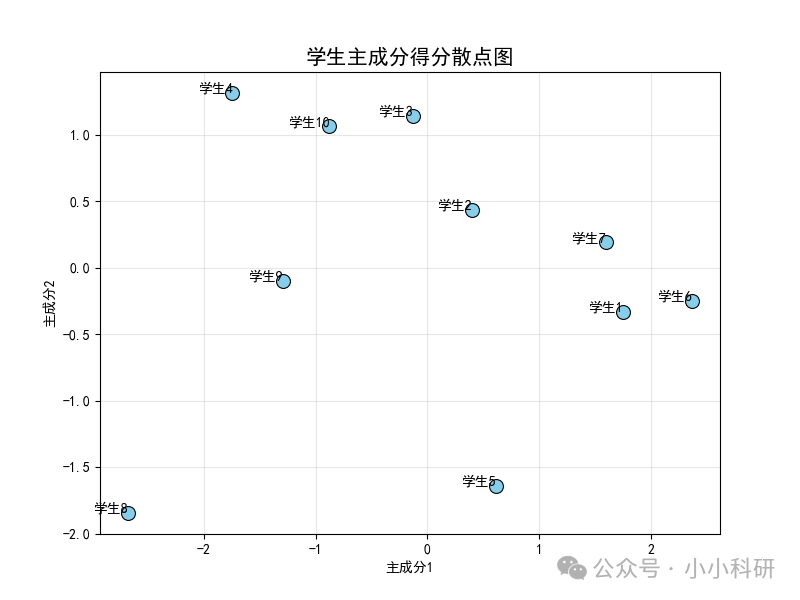
plt.show()

从下图中，能直观区分学生偏科特点，比如学生3 在“主成分2（文科倾向）”轴得分高，学生6在 “主成分 1（理科倾向）”轴得分高。

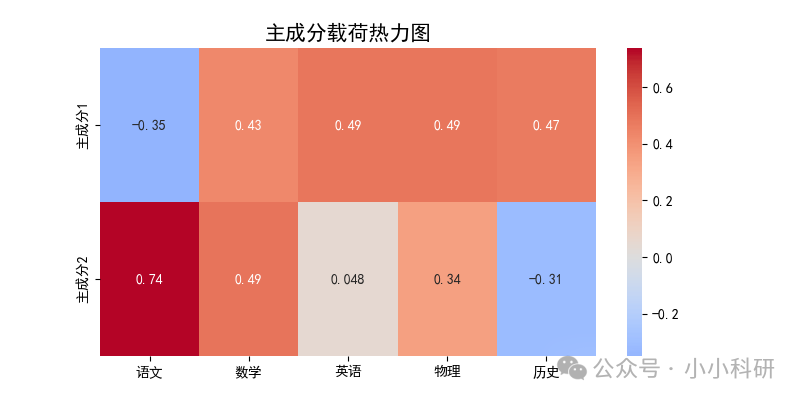
通过观察下图颜色深浅，可以清晰呈现主成分与原始科目间的关联——主成分1与英语、物理、历史权重高，主成分2与语文、数学权重高。主成分1的学生可能在主科（语文数学英语）中表现较差，在物理、历史科目上表现较优，主成分2的学生可能在主科上表现较优，在物理和历史科目上略逊一筹。

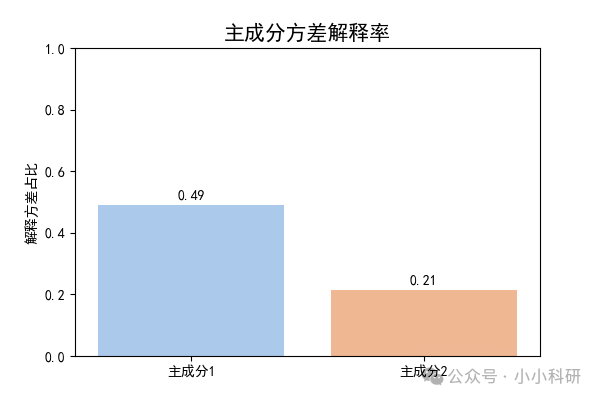
主成分1解释49%数据信息，主成分 2解释21%，两者共占70%，说明主成分1和2有效解释了70%的样本，降维效果较好。

四、因子分析实操

代码生成20条消费者对产品的评价数据，包括包装、设计、价格、性价比、售后5个方面。

import numpy as np
import pandas as pd
import statsmodels.api as sm
from statsmodels.multivariate.factor import Factor
import matplotlib.pyplot as plt
import seaborn as sns
# 设置中文显示
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题
# 步骤1：生成随机数据
np.random.seed(42)  # 固定随机种子
# 生成相关数据：A和B相关，C和D相关，E独立
A = np.random.uniform(2, 4, 20)  # 包装评分
B = A + np.random.normal(0, 0.3, 20)  # 设计评分（和A相关）
C = np.random.uniform(1.5, 3.5, 20)  # 价格评分
D = C + np.random.normal(0, 0.2, 20)  # 性价比评分（和C相关）
E = np.random.uniform(2, 4, 20)  # 售后评分（独立）
# 整理成DataFrame
eval_df = pd.DataFrame({
    'A_包装': A.round(1),
    'B_设计': B.round(1),
    'C_价格': C.round(1),
    'D_性价比': D.round(1),
    'E_售后': E.round(1)
})
print("消费者评价数据（前5行）：")
print(eval_df.head())
# 步骤2：用因子分析提取潜在因子
# 1. 拟合因子模型（假设2个潜在因子，修正参数为n_factor）
factor_model = Factor(eval_df, n_factor=2).fit()  # 此处将nfactors改为n_factor
# 2. 查看变量在因子上的载荷（关联强度）
factor_loadings = pd.DataFrame(
    factor_model.loadings,
    columns=['因子1', '因子2'],
    index=eval_df.columns
)
print("\n因子载荷（关联强度）：")
print(factor_loadings.round(2))
# 步骤3：可视化分析结果
# 1. 因子载荷热力图
plt.figure(figsize=(8, 4))
sns.heatmap(factor_loadings, annot=True, cmap='viridis', center=0, vmin=-1, vmax=1)
plt.title('因子载荷热力图', fontsize=15)
plt.show()
# 2. 变量-因子关系散点图（因子载荷图）
plt.figure(figsize=(8, 6))
for i, var in enumerate(factor_loadings.index):
    plt.scatter(
        factor_loadings['因子1'].iloc[i],
        factor_loadings['因子2'].iloc[i],
        s=100,
        label=var
    )
    plt.text(
        factor_loadings['因子1'].iloc[i]+0.05,
        factor_loadings['因子2'].iloc[i]+0.05,
        var,
        fontsize=10
    )
plt.xlabel('因子1')
plt.ylabel('因子2')
plt.axhline(0, color='gray', linestyle='--', alpha=0.5)
plt.axvline(0, color='gray', linestyle='--', alpha=0.5)
plt.title('变量-因子关系散点图', fontsize=15)
plt.grid(alpha=0.3)
plt.legend(loc='lower left')
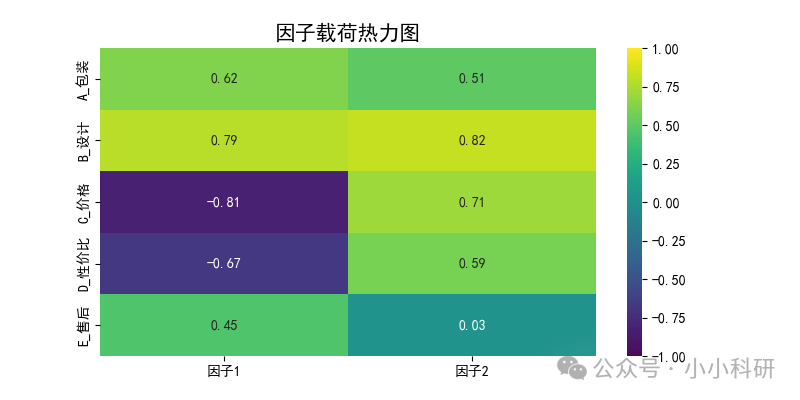
plt.show()

由下图可以看出，A_包装、B_设计、E_售后在因子 1 上载荷高（0.62、0.79、0.45），C_价格、D_性价比在因子 2 上载荷高（0.71、0.59），直观呈现变量与因子的归属关系。

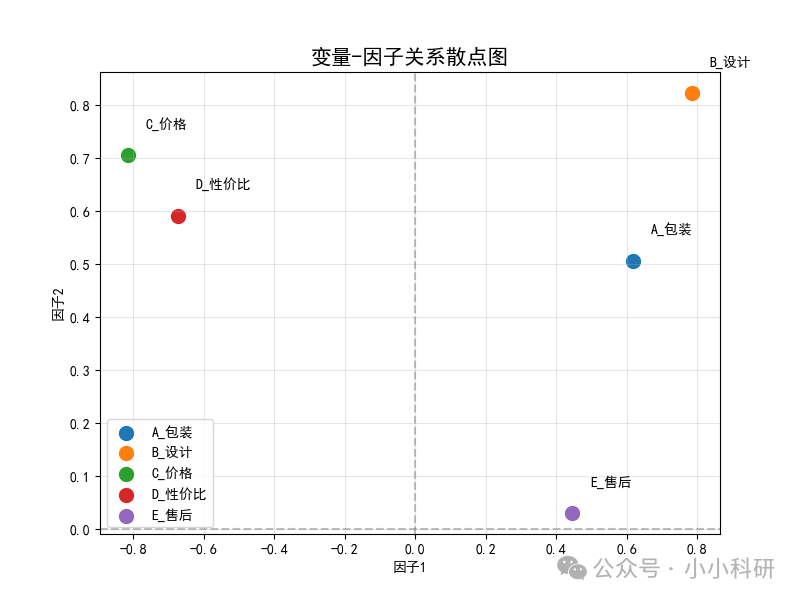
如下图，A_包装与 B_设计在图中聚集（对应 “外观评价因子”），C_价格与 D_性价比聚集（对应 “价值评价因子”），E_售后单独分布，清晰体现潜在因子的分组逻辑。

并得出因子方程分别为：

（推断为产品外观与服务因子）

（推断为产品价值因子）

https://mp.weixin.qq.com/s/1HBXJ8Ev1oHE4jQ7gRrI2whttps://mp.weixin.qq.com/s/1HBXJ8Ev1oHE4jQ7gRrI2w

请点击上方链接，关注【小小科研】公众号，了解更多模型哦，感谢支持！