目录
一、情景导入:网购时的 “隐形军师”
你有没有发现,打开购物软件时,总会收到一些“猜你想买”的推荐?比如你最近搜了几次运动鞋,首页就会跳出几款适合你的款式。其实,背后可能就有逻辑回归在帮忙——平台通过分析你过往的浏览记录、收藏行为、消费能力等数据,判断你“是否会购买某件商品”,再把可能性高的商品推给你。
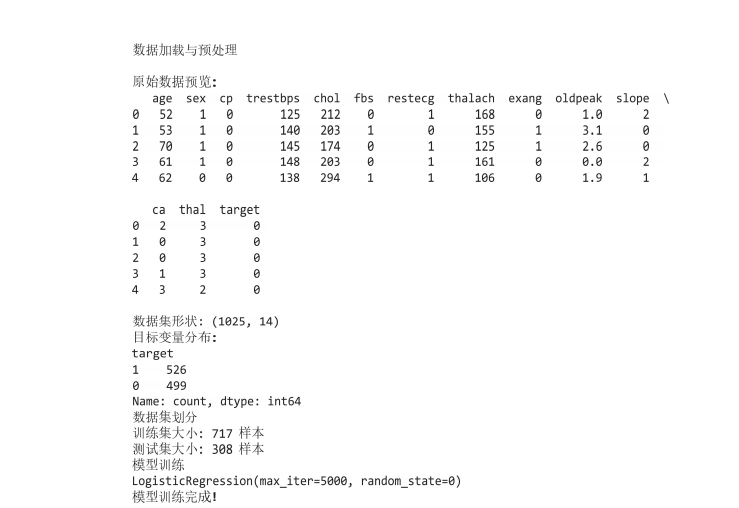
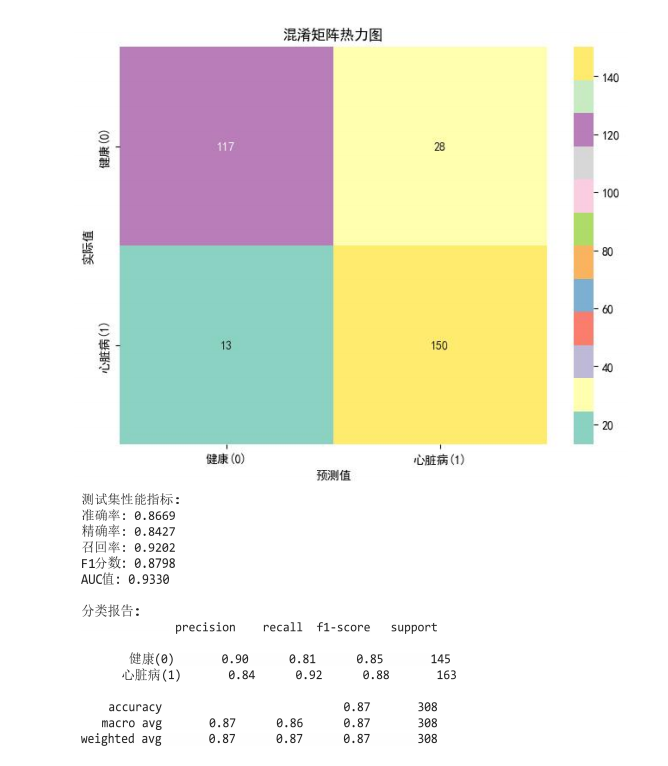
这和下文实战操作案例里用逻辑回归预测心脏病的思路很像。实战操作案例中用 1025 名患者的年龄、血压等 14 项数据,来判断一个人 “是否有心脏病”,最终模型对 308 名测试者的判断准确率达到了 86.69%。生活中,这种 “用数据做二选一判断” 的场景,逻辑回归都能派上用场。
二、模型介绍:简单又靠谱的 “分类工具”
逻辑回归虽然名字里带“回归”,但它其实是个专门解决“二分类问题”的模型——也就是处理只有两种结果的情况,比如“买/不买”“患病/健康”“通过/不通过”。
在下文实战操作案例中,用逻辑回归来区“健康(0)”和“心脏病(1)”:先从 Excel文件中读取数据,把数据分成两部分(717 个样本用于训练模型,308 个样本用于测试),再用LogisticRegression工具训练模型,让它从数据中学习规律。训练好的模型能根据新数据给出判断,比如对新患者的生理指标进行分析,输出“有心脏病”或“健康”的结果。
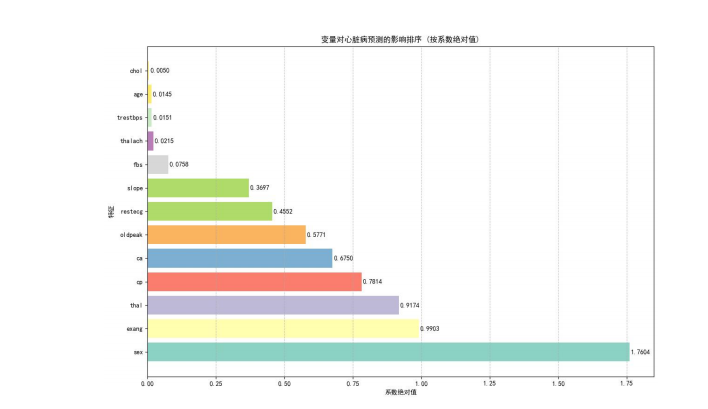
它的最大优点是“简单易懂”,不像有些复杂模型那样“黑箱操作”,而是能清楚告诉你“哪些因素影响最大”,这也是它在实际中常用的原因。
三、模型原理:从数据到判断的五步走
逻辑回归(Logistic Regression)是一种广泛应用于二分类问题的统计学习方法,其核心是通过 sigmoid 函数将线性回归的输出映射到[0,1]区间,从而实现对类别概率的预测。
1. 挑选关键因素,算出“影响总分”
首先确定哪些因素会影响结果。比如预测心脏病时,年龄、性别、胸痛类型等都是关键因素;就像文档里用到的 14 项特征一样。然后给每个因素分配一个“权重”(系数),越重要的因素权重越大。
把“因素值 × 权重”加起来,再加上一个基础值(截距),就能得到一个“影响总分”(z 值)。

2. 用 Sigmoid 函数,把总分转成概率
“影响总分” 可能是任意数字,而我们需要的是“这件事发生的概率”(0到1之间)。这时候就需要 Sigmoid 函数来转换。

比如实战操作案例中,当 z 值计算完成后,代入这个公式就能得到“患心脏病的概率”。这个函数像个“翻译器”,把抽象的总分变成了直观的可能性。
3. 决策边界
有了概率预测后,需要通过决策阈值(通常取 0.5)将概率转化为类别:

有了概率后,需要一个 “判断标准”。通常把阈值设为 0.5:如果概率>0.5,就判断为“会发生”(比如有心脏病);否则判断为“不会发生”(比如健康)。
实操操作案例中对新样本的预测就是这么做的:概率 0.607 的样本被判断为“心脏病(1)”,概率 0.007 的样本被判断为“健康(0)”。
4. 模型训练:极大似然估计
逻辑回归通过极大似然估计求解最优参数w和b,目标是使训练数据的“似然性”最大(即模型对训练样本的预测概率尽可能高)。

5.多分类逻辑回归
逻辑回归可扩展到多分类问题(如手写数字识别,10 个类别),常用方法为softmax 回归:

逻辑回归是广义线性模型的一种,核心是用sigmoid函数将线性输出转化为概率;适用于二分类问题,通过softmax可扩展到多分类;模型简单、可解释性强(权重w可表示特征对结果的影响程度),广泛应用于金融风控、医疗诊断、营销预测等领域。其本质是通过学习特征与类别概率的线性关系,实现对分类边界的建模。
四、应用场景:生活中处处都能“用得上”
逻辑回归就像一个“万能判断仪”,在很多场景中都能发挥作用:
- 医疗健康:除了文档中的心脏病预测,还能通过体检数据判断“是否有糖尿病风险”“是否需要进一步检查” 等,辅助医生做决策;
- 信贷审核:银行用它分析申请人的收入、负债等数据,判断“是否会违约”,决定要不要放贷;
- 内容推荐:视频平台根据你的观看记录,判断“是否喜欢某类视频”,精准推送内容;
- 品质检测:工厂通过产品的尺寸、材质等数据,判断“是否为合格品”,提高质检效率。
不管是治病救人还是日常消费,逻辑回归都在用简单的数学原理,帮我们把复杂的判断变得更精准。
五、实战操作































 596
596

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








