省选专练之后缀数组 HihoCoder-1403 后缀数组一·重复旋律

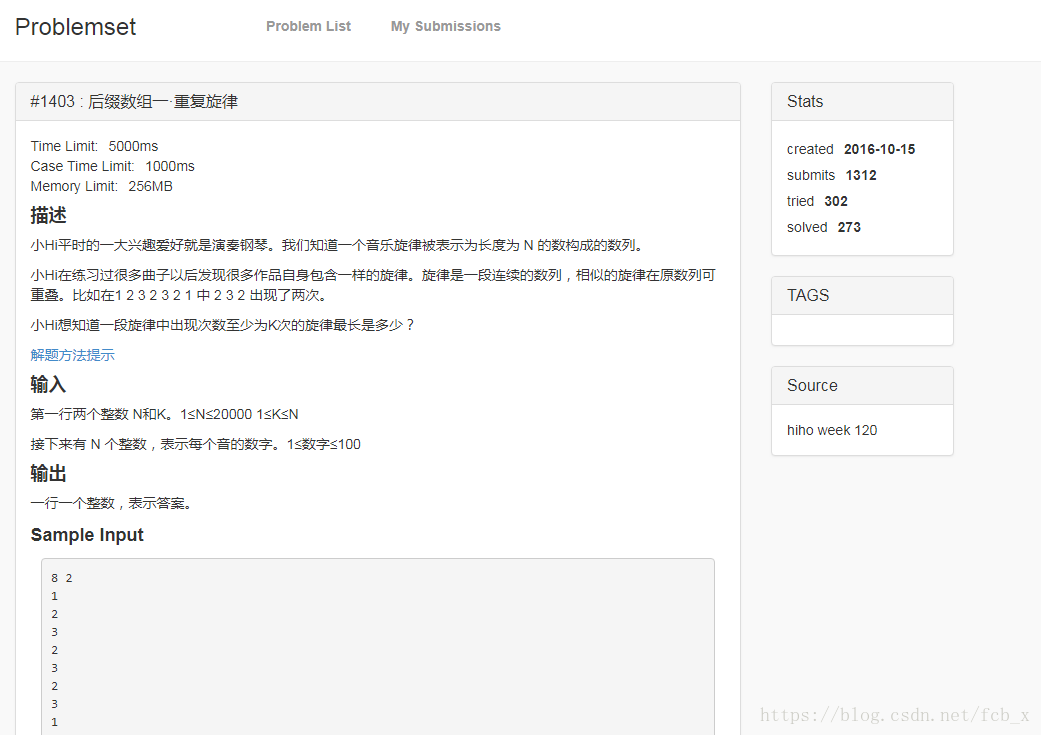
后缀数组板子题

额这个实际上考察的是height数组的应用

本质来说就是如果有一段连续为k-1的数组那么存在一个LCP满足条件

所以说构建SA并且二分答案就完了

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+100;
int S[N]={};
int c[N]={};
int x[N]={};
int y[N]={};
int SA[N]={};
int rk[N]={};
int height[N]={};
int n,m=100;
void Get_SA(){
	for(int i=1;i<=n;++i)x[i]=S[i];
	for(int i=1;i<=n;++i)c[x[i]]++;
	for(int i=1;i<=m;++i)c[i]+=c[i-1];
	for(int i=n;i>=1;--i)SA[c[x[i]]--]=i;
	for(int k=1;k<=n;k=k<<1){
		int num=0;
		for(int i=n-k+1;i<=n;++i)y[++num]=i;
		for(int i=1;i<=n;++i)if(SA[i]>k)y[++num]=SA[i]-k;
		for(int i=1;i<=m;++i)c[i]=0;
		for(int i=1;i<=n;++i)c[x[i]]++;
		for(int i=1;i<=m;++i)c[i]+=c[i-1];
		for(int i=n;i>=1;--i)SA[c[x[y[i]]]--]=y[i],y[i]=0;
		swap(x,y);
		x[SA[1]]=1;
		num=1;
		for(int i=2;i<=n;++i)x[SA[i]]=(y[SA[i]]==y[SA[i-1]]&&y[SA[i]+k]==y[SA[i-1]+k])?num:++num;
		if(num==n)break;
		m=num;
	}
}
void Get_Height(){
	for(int i=1;i<=n;i++)rk[SA[i]]=i;
	int k=0;
	for(int i=1;i<=n;i++){
		if(rk[i]==1)continue;
		if(k)k--;
		int Id=SA[rk[i]-1];
		while(Id+k<=n&&i+k<=n&&S[Id+k]==S[i+k])++k;
		height[rk[i]]=k;
	}
}
int k;
bool check(int sum){
	int len=0;
	for(int i=2;i<=n;i++){
		if(height[i]>=sum){
			++len;
			if(len>=k)return true;
		}
		else len=0;
	}
	return false;
}
int main(){
	freopen("test.in","r",stdin);
	scanf("%d%d",&n,&k);
	k--;
	for(int i=1;i<=n;i++)scanf("%d",&S[i]);
	Get_SA();
	Get_Height();
	int l=1;
	int r=n+1;
	int ans=0;
	while(l<=r){
		int mid=(l+r)/2;
		if(check(mid)){
			l=mid+1;
			ans=mid;
		}
		else r=mid-1;
	}
	cout<<ans;
}