随机特征方法 RFM｜AI for PDE 的技术路线上可能不⽌有 PINN

求解偏微分方程（Partial Differential Equation, PDE）是科学计算领域最重要的课题之一，也是计算机辅助工程（Computer-Aided Engineering, CAE）软件的核心要素。为求解 PDE，有限差分方法、有限元方法、谱方法等经典数值方法被提出并广泛研究。但是，经典数值方法依赖于网格离散，在复杂几何和高维问题等方面面临困难。

在 AI for Science 时代，AI 模型在很多任务上取得了巨大成功，使用这些模型来求解 PDE 的想法也得到了许多学者的青睐。一个最为直接的思路是利用考虑物理约束的深度神经网络来表示 PDE 的解，并利用 PDE 结构定义损失函数、优化神经网络。以此为基础发展的最有代表性的方法是已经得到广泛关注、被寄予厚望的物理信息神经网络（Physics-Informed Neural Networks, PINN）。

然而，值得关注的是，神经网络比较明显的优势在处理高维问题上。PDE 的大量实际应用场景所面临的挑战不在维数灾难上，而在几何复杂、多尺度等方面。此时，神经网络的优势不容易发挥出来，反倒因为非线性优化等方面的困难，面临着求解效率低、误差不可控、难以系统改进等挑战。因此，如何融合经典数值方法与机器学习方法的优势，是一个亟待解决的问题。在这个大背景下，陈景润、池煦荣、鄂维南、杨周旺四位学者于 2022 年提出随机特征方法（The Random Feature Method, RFM）。RFM 在避免网格生成、容易处理复杂几何区域（如图1）的同时，也在各种场景下都有媲美经典数值方法的精度和效率（如图2）。

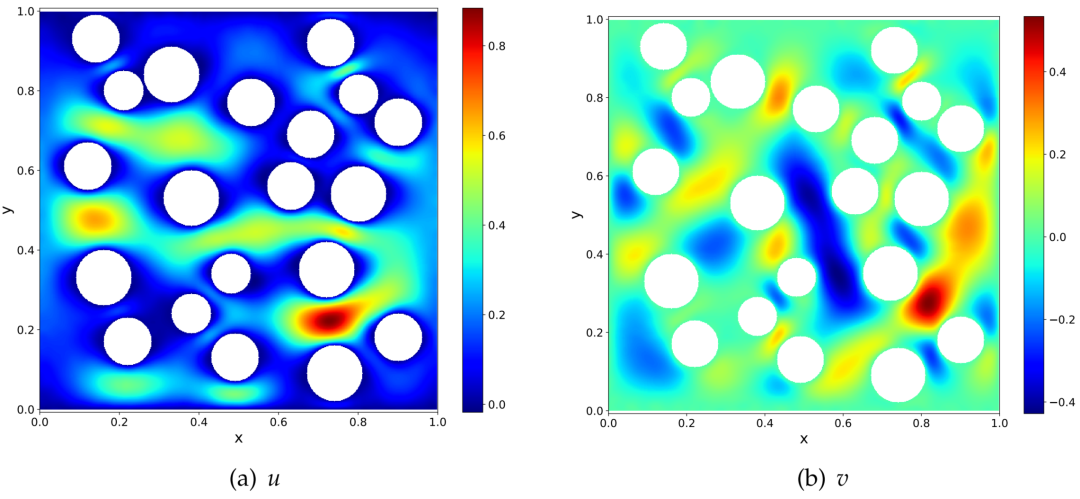
                    图1：RFM在2维复杂几何区域上的稳态S