FPGA教程系列-CRC校验初识

原创已于 2025-12-04 19:43:00 修改 · 176 阅读

7 ·

CC 4.0 BY-SA版权

文章标签：

#信号

于 2025-12-04 19:42:13 首次发布

FPGA教程系列专栏收录该内容

23 篇文章

订阅专栏

FPGA教程系列-CRC校验初识-N

在学习CRC的时候，不得不感慨二进制的特殊之处，传统的十进制的思维在这里受到了限制，同时又联想到了小谢尔顿的梦境，梦到了真神，0和1，万事万物都可以简单的用0和1来表示，希望能够把思维拓展开来。

细节在这里，好文章推荐。根据文章

https://mp.weixin.qq.com/s/sUf-_N31g-nkpYb_wvZpDw

目的

为了错误检验，信息在传递的过程中避免不了出错，如何检验数据的正确性，才需要一种校验的方法，串口通信的校验码等等都是如此。

发送方会根据消息本身计算出一个特定的值（叫做校验和，checksum），然后把它加到消息后面一起发出去。
接收方收到消息后，用同样的计算方法，再算一遍校验和，然后和消息中附带的校验和对比一下。

一样 → 说明很可能没出错。
不一样 → 说明传输过程中有数据被改了。

即使是有了校验的方法，仍然不可避免的会产生错误，校验方法并不是一成不变的，所以需要根据实际的应用场景进行选择。

一个强的校验和算法至少需要满足两个条件：

宽度 (WIDTH) ：寄存器要够宽，降低理论上的漏检概率。比如 32 位宽 → 漏检概率 1/2³²。
混乱度 (CHAOS) ：公式要够“乱”，让每个输入字节都有机会改动寄存器的任意一位。

加法校验存在一定的缺陷，因此人们发明了CRC校验，虽然不是完美的，但应该减少了很多的错误发生的机会。

除法校验

CRC（循环冗余校验）的核心思想就是：

把整个消息看作一个超大的二进制数；
用一个固定的二进制数（多项式）去除它；
把余数作为校验和。

发送的数据是（原消息） + （校验和），优势：

在加法里，每个输入字节对寄存器的影响很局限；
在除法里，每一位数据都会让余数在计算过程中被“搅动”，而且随着数据变长，余数会快速发生巨大变化；
这种“混乱度”让漏检错误的概率大大降低。

CRC 算法里的“多项式”是怎么回事？

把二进制数看作一个多项式的系数序列（通俗讲就是把二进制数变成多项式的形式） 。文章里关于这部分写的比较清楚了，就不再赘述。

重点是CRC用的是模2&无进位，习惯用十进制考虑话就类似于9+1=0.

而二进制里的异或算法就代表了加法或者减法。XOR

用多项式只是数学上方便推导 CRC 的方式，但在实际实现时，直接用无进位二进制运算（XOR）就够了

不断把某个固定模式（poly）在不同位置 XOR 进数据里（通俗的讲（信息+CRC校验）是可以被poly整除的，不能整除CRC校验就错了）
这样既能构造倍数，也能做除法检测。

CRC 计算的完整步骤

选择一个多项式（poly）
准备消息
在 CRC 算术（无进位 XOR）下做二进制长除法
得到 CRC 校验码
发送数据
接收端校验方式

看了例子没太理解，重新理解一遍：

CRC 算术的基本规则（无进位运算）

1、加法=减法=异或操作，传统的十进制的思维下，很难去理解，加法=减法，因为即使是无进位，9+1=0，9-1=8，也不能说明加法与减法是一致的，但是在二进制内却不一样，0-1=1，0+1=1，应该算是二进制的一个比较独特的性质，正好与计算机的二极管性质一致，也算是大自然的牛逼之处吧？

2、大小失效：简单的理解就是既然加法减法一样，自然无法比较两个数的大小了。

3、CRC 乘法就是按位移后的加法（XOR）求和：

4、除法：CRC 除法类似长除法，但判断“能除”是用最高位 1 的位置来比较的：

如果被除数的最高位 1 在同一位置或更高，就能除。

简单CRC算法

文章里写的很清楚了，也没有太多的疑问，关于poly的选择，只能说按前人的经验就好，感觉也不用过多的去理解，需要的时候再重新回顾一下吧。

核心思路

用一个W 位的寄存器（W = 多项式最高位位置）
依次把消息的每一位（加上 W 个 0 的“尾巴”）送进寄存器
每次移位后，如果左端（最高位）弹出的是 1，就执行一次寄存器 XOR 多项式
最后寄存器中的值就是CRC 校验值

以 Poly=11011，W=4 为例：

Poly 除最高位外的部分是1011
消息 = 1101（按位高到低依次送入）
每当最高位溢出 1，就R = R XOR 1011
最后 R 的内容就是 CRC 值 1000

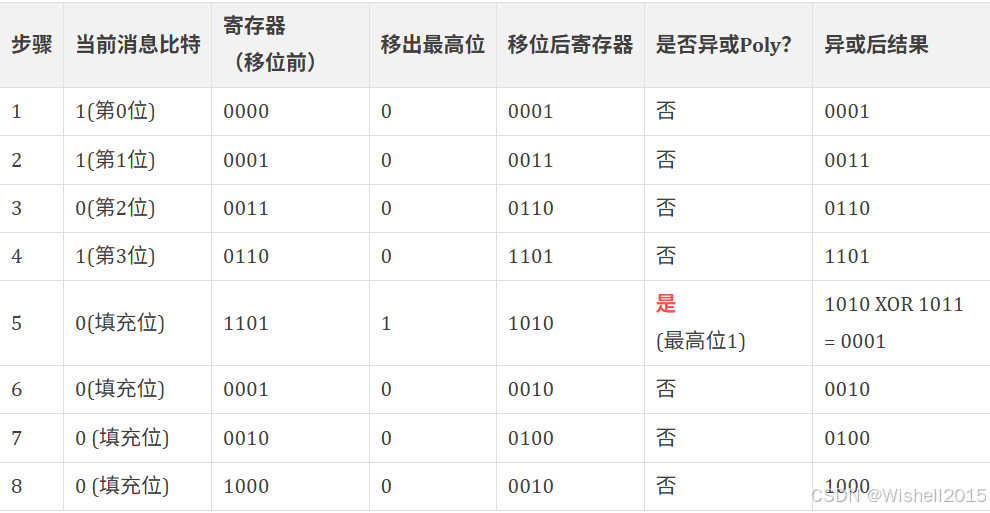
对照表类似于做了一个长除法

                   ...商不关心...
        _______________________
11011 ) 11010000     ← 原始消息左移 4 位
        11011          XOR 第 1 次
        -----
         000010000
            11011     XOR 第 2 次
            -----
             1110      ← 余数，正是寄存器里的 1000