2.4 卷积1
2.4 卷积
在了解了系统及其脉冲响应之后,人们可能会想知道是否有一种方法可以通过任何给定的输入信号(不仅仅是单位脉冲)确定系统的输出信号。卷积就是这个问题的答案,前提是系统是线性且时不变的(LTI)。
Tips:大概是卷积的意义吧,由输入确定系统的输出。
2.4.1 常规卷积
我们从实际信号和具有实际脉冲响应的LTI系统开始。
假设我们有一个任意信号 s[n]s[n]s[n]。然后,s[n]s[n]s[n] 可以通过以下逻辑分解为平移单位脉冲的缩放和。将 s[n]s[n]s[n] 与一个单位脉冲相乘,脉冲被平移了 mmm 个样本,即 δ[n−m]\delta[n - m]δ[n−m]。由于 δ[n−m]\delta[n - m]δ[n−m] 在除了 n=mn = mn=m 之外的所有地方都等于 0,这将使得所有的 s[n]s[n]s[n] 值在 n≠mn \neq mn=m 时乘以 0,而在 n=mn = mn=m 时乘以 1。因此,结果序列将在 n=mn = mn=m 处具有一个脉冲,其值等于 s[m]s[m]s[m]。这一过程在图2.6中得到了清晰的说明。

图2.6:将信号 s[n]s[n]s[n] 与一个偏移 mmm 的单位冲激信号相乘
可以数学地表示为:
$$s[n] \delta[n - m] = s[m] \delta[n - m]$$用另一个偏移 m′m'm′ 重复相同的过程,得到:
$$s[n] \delta[n - m'] = s[m'] \delta[n - m']$$我们说,此时提取出值 s[m′]s[m']s[m′]。因此,如果这个乘法过程在所有可能的延迟 −∞<m<∞-\infty < m < \infty−∞<m<∞ 上重复,并且所有生成的信号相加在一起,结果将是序列 s[n]s[n]s[n] 本身。
$$s[n] = \cdots + s[-2]\delta[n+2] + s[-1]\delta[n+1] + s[0]\delta[n] + s[1]\delta[n-1] + s[2]\delta[n-2] + \cdots$$$$= \sum_{m=-\infty}^{\infty} s[m] \delta[n-m] \tag{2.3}$$总结来说,上述方程表明,信号 s[n]s[n]s[n] 可以表示为加权单位冲激信号的和,其中每个单位冲激信号 δ[n−m]\delta[n - m]δ[n−m] 的幅度为 s[m]s[m]s[m]。这样的和的一个例子如图2.7所示。
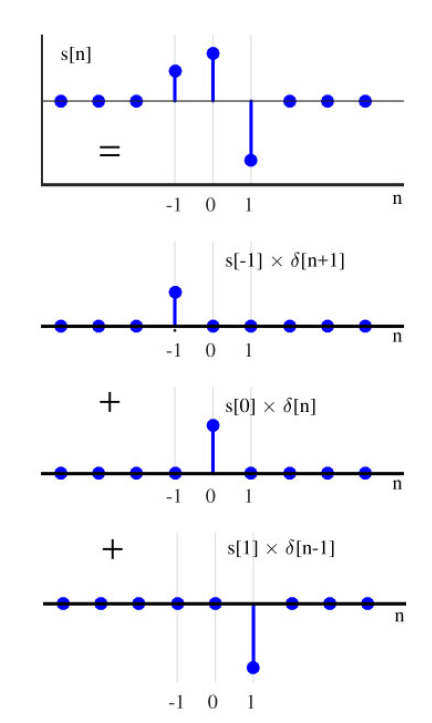
图2.7:将信号 s[n]s[n]s[n] 分解为缩放和偏移的冲激信号
LTI系统对缩放单位冲激的响应
现在考虑当这样的信号作为输入给具有冲激响应 h[n]h[n]h[n] 的LTI系统时会发生什么。
- 冲激响应 —— LTI系统对单位冲激 δ[n]\delta[n]δ[n] 的响应是 h[n]h[n]h[n]。
- 由于时不变性,系统对一个移位的单位冲激 δ[n−m]\delta[n - m]δ[n−m] 的响应是 h[n−m]h[n - m]h[n−m]。
- 由于线性特性的缩放性质,系统对一个缩放并移位的单位冲激 s[m]⋅δ[n−m]s[m] \cdot \delta[n - m]s[m]⋅δ[n−m] 的响应是 s[m]⋅h[n−m]s[m] \cdot h[n - m]s[m]⋅h[n−m]。
- 由于线性特性的加法性质,系统对多个移位单位冲激的响应是各自输出的总和。
输入 —— 输出 对应关系:
| 输入 | 输出 |
|---|---|
| δ[n]\delta[n]δ[n] | h[n]h[n]h[n] |
| δ[n−m]\delta[n - m]δ[n−m] | h[n−m]h[n - m]h[n−m] |
| α1⋅δ[n−m]\alpha_1 \cdot \delta[n - m]α1⋅δ[n−m] | α1⋅h[n−m]\alpha_1 \cdot h[n - m]α1⋅h[n−m] |
| α2⋅δ[n−m′]\alpha_2 \cdot \delta[n - m']α2⋅δ[n−m′] | α2⋅h[n−m′]\alpha_2 \cdot h[n - m']α2⋅h[n−m′] |
| α1⋅δ[n−m]+α2⋅δ[n−m′]\alpha_1 \cdot \delta[n - m] + \alpha_2 \cdot \delta[n - m']α1⋅δ[n−m]+α2⋅δ[n−m′] | α1⋅h[n−m]+α2⋅h[n−m′]\alpha_1 \cdot h[n - m] + \alpha_2 \cdot h[n - m']α1⋅h[n−m]+α2⋅h[n−m′] |
这导致了一个输入-输出序列为:
$$\begin{aligned} &+ ....... & \rightarrow & \quad ....... \\ &+ \quad s[-2] \cdot \delta[n + 2] & \rightarrow & \quad s[-2] \cdot h[n + 2] \\ &+ \quad s[-1] \cdot \delta[n + 1] & \rightarrow & \quad s[-1] \cdot h[n + 1] \\ &+ \quad s[0] \cdot \delta[n] & \rightarrow & \quad s[0] \cdot h[n] \\ &+ \quad s[1] \cdot \delta[n - 1] & \rightarrow & \quad s[1] \cdot h[n - 1] \\ &+ \quad s[2] \cdot \delta[n - 2] & \rightarrow & \quad s[2] \cdot h[n - 2] \\ &+ \quad ....... & \rightarrow & \quad ....... \\ \end{aligned}$$- 最终: s[n]s[n]s[n] → ∑m=−∞∞s[m]⋅h[n−m]\sum_{m=-\infty}^{\infty} s[m] \cdot h[n - m]∑m=−∞∞s[m]⋅h[n−m]
在上面的过程中,我们推导出了著名的卷积方程,用来描述当输入信号 s[n]s[n]s[n] 经过具有冲激响应 h[n]h[n]h[n] 的LTI系统时,输出 r[n]r[n]r[n] 的表达式:
$$r[n] = \sum_{m=-\infty}^{\infty} s[m] \cdot h[n - m] \quad \tag{2.4}$$其中上面的和式是从 −∞-\infty−∞ 到 +∞+\infty+∞ 对每个 nnn 计算的。在本文中,卷积操作表示为 ∗*∗,即:
$$r[n] = s[n] * h[n] \quad \tag{2.5}$$注意,卷积与相关不同的是:
$$s[n] * h[n] = h[n] * s[n]= \sum_{m=-\infty}^{\infty} h[m]s[n-m] \tag {2.6}$$这可以通过在公式 (2.4) 中代入 p=n−mp = n - mp=n−m 来验证,得到 m=n−pm = n - pm=n−p,因此∑p=−∞∞s[n−p]h[p]\sum_{p=-\infty}^{\infty} s[n - p] h[p]∑p=−∞∞s[n−p]h[p]
注释 2.3 卷积符号
请记住,虽然卷积和信号的共轭都用符号 ∗*∗ 表示,但在上下文中总是能看到它们的区别。当用于卷积时,它作为两个信号之间的运算符出现,例如 s[n]∗h[n]s[n] * h[n]s[n]∗h[n]。另一方面,当用于共轭时,它出现在信号的上标处,例如 h∗[n]h^*[n]h∗[n]。
卷积是一个非常逻辑且简单的过程,但许多数字信号处理(DSP)学习者由于解释方式的缘故,可能会感到困惑。接下来,我们将描述一种传统的方法和另一种更直观的方法来计算卷积输出。
传统方法
在定义卷积方程后,建议通过以下步骤来实现。对于每个特定时间移位 nnn,步骤如下:
-
翻转 (Flip) :将卷积方程排列为
r[n]=∑m=−∞∞s[m]h[−m+n]r[n] = \sum_{m=-\infty}^{\infty} s[m] h[-m + n]r[n]=∑m=−∞∞s[m]h[−m+n]并将冲激响应 h[m]h[m]h[m] 视为变量 mmm 的函数。将 h[m]h[m]h[m] 关于 m=0m = 0m=0 翻转以得到 h[−m]h[-m]h[−m]。
-
移位 (Shift) :为了得到时间移位 nnn 时的 h[−m+n]h[-m + n]h[−m+n],将 h[−m]h[-m]h[−m] 向右移 nnn 个单位(对于正 nnn),对于负 nnn 则向左移。
-
相乘 (Multiply) :将序列 s[m]s[m]s[m] 与序列 h[−m+n]h[-m + n]h[−m+n] 逐点相乘,得到乘积序列 s[m]⋅h[−m+n]s[m] \cdot h[-m + n]s[m]⋅h[−m+n]。
-
求和 (Sum) :将上述乘积序列的所有值相加,得到在时间 nnn 时的卷积输出。
-
重复 (Repeat) :对每个可能的 nnn 值重复上述步骤。
两个信号之间卷积的示例
$$s[n] = [2, -1, 1]$$$$h[n] = [-1, 1, 2]$$如图 2.8 所示。在左边的列中,信号 s[m]s[m]s[m] 被复制并与 h[−m]h[-m]h[−m] 的移位版本叠加,以演示两者之间的重叠,而移位 nnn 则显示在文本框中对应每个 nnn 的值。如果你按照上述步骤操作,你会在图的右边列的文本框中找到结果 r[n]r[n]r[n]:
$$r[n] = [-2, 3, 2, -1, 2]$$请注意上面信号表示中的变化。实际的信号 s[n]s[n]s[n] 和 h[n]h[n]h[n] 是时间索引 nnn 的函数,但卷积方程表示的是这两个信号在时间索引 mmm 下的卷积。另一方面,nnn 用于表示在逐点与 s[m]s[m]s[m] 相乘之前,应用于 h[−m]h[-m]h[−m] 的时间移位。输出 r[n]r[n]r[n] 是时间索引 nnn 的函数,这对应于应用于 h[−m]h[-m]h[−m] 的移位。
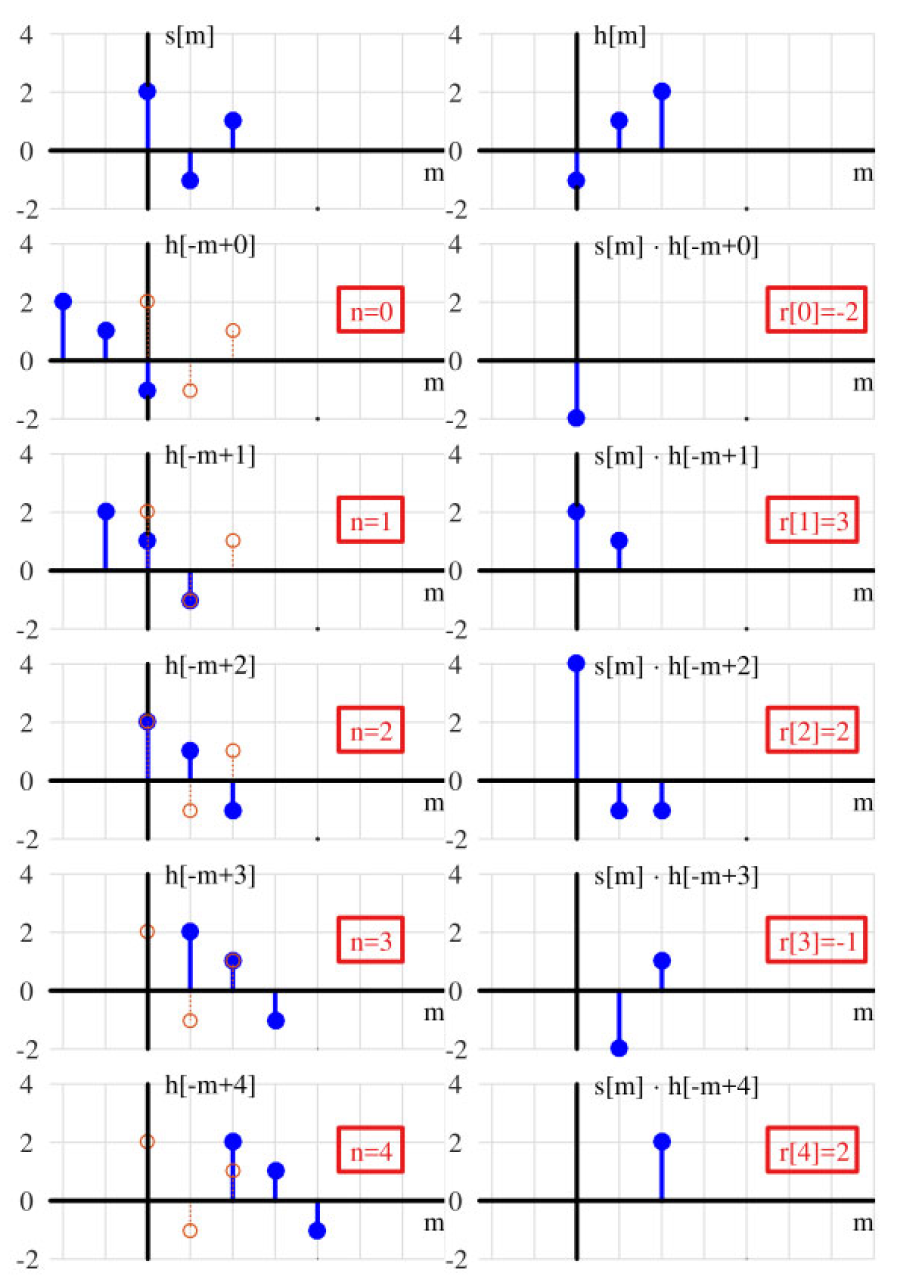
图 2.8: s[n] 和 h[n] 之间卷积的传统方法
接下来,我们转向一种更直观的方法,在这种方法中不需要翻转信号。
直观方法
理解卷积的另一种方法。实际上,它是建立在卷积方程 (2.4) 的推导基础上的,也就是找到输出 r[n]r[n]r[n] ,其表达式为:
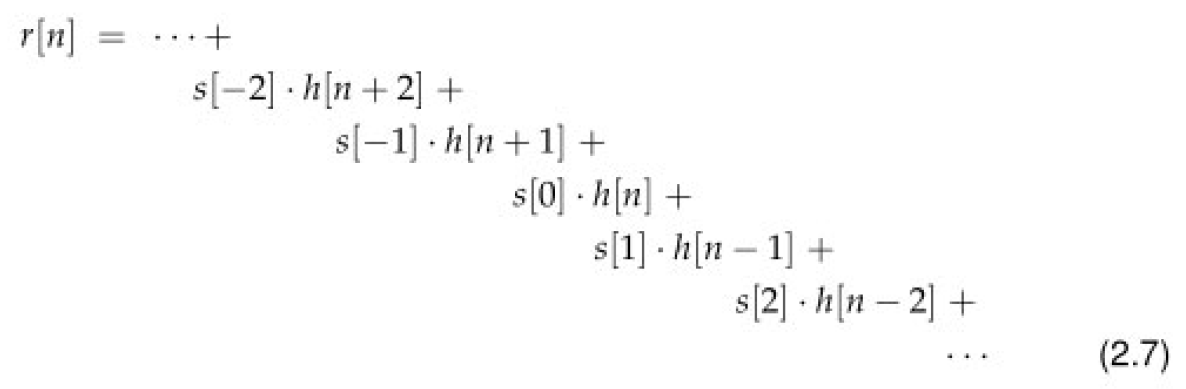
让我们解决与图 2.8 相同的例子,其中
s[n]=[2,−1,1]s[n] = [2, -1, 1]s[n]=[2,−1,1]
h[n]=[−1,1,2]h[n] = [-1, 1, 2]h[n]=[−1,1,2]
表 2.1: s[n] 和 h[n] 之间卷积的直观方法
| nnn | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| s[n]s[n]s[n] | 2 | -1 | 1 | ||
| s[0]⋅h[n]s[0] \cdot h[n]s[0]⋅h[n] | 2(-1) | 2(1) | 2(2) | ||
| s[1]⋅h[n−1]s[1] \cdot h[n-1]s[1]⋅h[n−1] | 0 | -1(-1) | -1(1) | -1(2) | |
| s[2]⋅h[n−2]s[2] \cdot h[n-2]s[2]⋅h[n−2] | 0 | 0 | 1(-1) | 1(1) | 1(2) |
| 输出 | -2 | 3 | 2 | -1 | 2 |
这种方法如表 2.1 和图 2.9 所示,其结果是通过列求和生成的。从实现的角度来看,这种方法与传统方法没有区别。
注释 2.4:翻转冲激响应的奇特案例
从上面的直观方法来看,翻转实际上根本不存在。翻转仅发生在时间索引 mmm 的世界中,而不是时间索引 nnn 的世界中。而我们在每个 nnn 上找到每个新的输出。
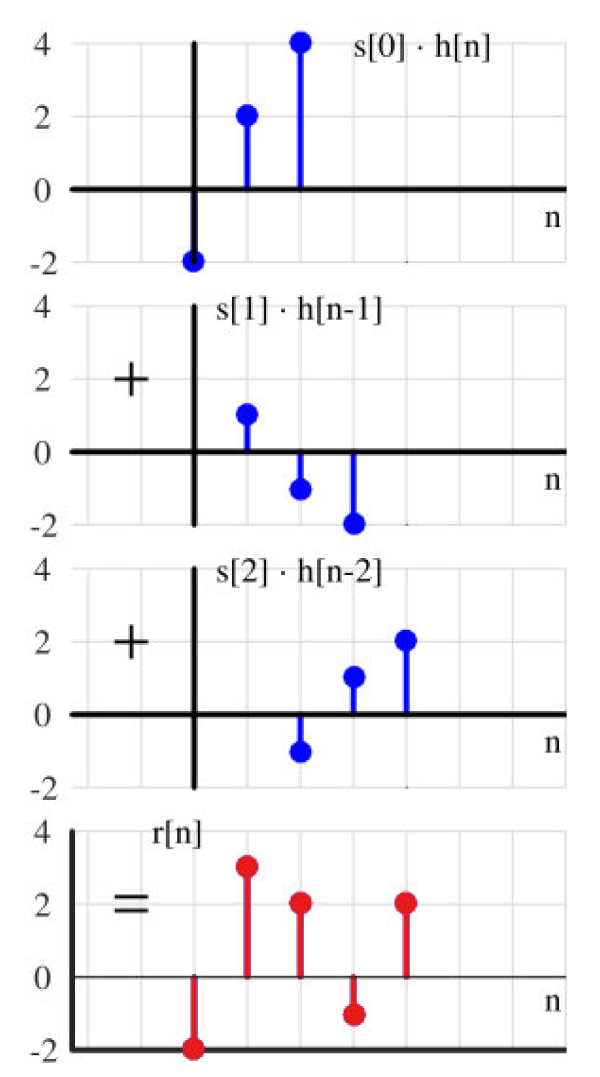
图 2.9: s[n] 和 h[n] 之间卷积的直观方法
现在(NOW),由卷积方程中 nnn 代表,即为自身的移动指针,这个指针实际上在过程中不断变化。时间在滴答流逝,每一次流逝,我们都能进入未来的一个单位,在那里新的输入到来并踢出另一个冲激响应(按输入在该瞬间的幅度缩放)。
由于在现在之前没有实际的输入可施加,我们从时间索引 0 开始。
- 输入 s[0]s[0]s[0] 在现在(NOW)贡献了 s[0]⋅h[0]s[0] \cdot h[0]s[0]⋅h[0],这是在时间 0 时的第一个输出采样。实际上,它启动了完整的冲激响应,该响应由其值 (s[0]⋅h[1],s[0]⋅h[2],⋯ )(s[0] \cdot h[1], s[0] \cdot h[2], \cdots)(s[0]⋅h[1],s[0]⋅h[2],⋯) 缩放,但这些将会发生在未来。
- 新的现在(NOW)是时间索引 1。输入 s[1]s[1]s[1] 到达并发起了完整的冲激响应,但只有 s[1]⋅h[0]s[1] \cdot h[0]s[1]⋅h[0] 发生在现在(NOW)。此外,向未来移动了 1 个单位意味着 s[0]⋅h[1]s[0] \cdot h[1]s[0]⋅h[1] 已在此时到达。因此,时间 1 的输出是 s[1]⋅h[0]+s[0]⋅h[1]s[1] \cdot h[0] + s[0] \cdot h[1]s[1]⋅h[0]+s[0]⋅h[1]。
- 以这种方式继续下去,可以看出,在卷积操作期间,现在(NOW) nnn 随着每个滴答向前推进。每个此类 nnn 激活新的冲激响应,当然从 h[0]h[0]h[0] 开始,因此表达式为 s[n]⋅h[0]s[n] \cdot h[0]s[n]⋅h[0]。只有过去输入的那些贡献可以在此时进行汇总,形成当前时刻的贡献。
显然,h[1]h[1]h[1] 将是从时间 n−1n-1n−1 发生的输入贡献,h[2]h[2]h[2] 来自 n−2n-2n−2 的输入,依此类推。总而言之,h[⋅]h[\cdot]h[⋅] 参数的论点不过是每个单独输入从现在(时间索引 nnn)的时间分离——由于这一记忆的存在,它发挥作用以找出每个过去输入对现在的影响。
性质
以下是卷积的一些重要性质。
长度 (Length) :从上图可以看出,当 s[n]s[n]s[n] 和 h[n]h[n]h[n] 的长度均为 3 个样本时,结果信号 r[n]r[n]r[n] 的长度为 5。这是一个通用规则:
$$\text{Length}\{r[n]\} = \text{Length}\{s[n]\} + \text{Length}\{h[n]\} - 1 \tag{2.8}$$这是由于在卷积过程中一个信号完全滑过另一个信号。
第一个样本 (First sample) :从翻转操作可以明显看出,结果的第一个样本位置由下式给出:
$$\text{First sample location}\{r[n]\} = \text{First sample location}\{s[n]\} + \text{First sample location}\{h[n]\} \tag{2.9}$$单位冲激 (Unit impulse) :由于单个单位冲激 δ[n]\delta[n]δ[n] 只能生成冲激响应 h[n]h[n]h[n] 的单一实例,因此单位冲激对冲激响应的卷积就是冲激响应本身。这个结果是通用的,适用于任何信号 s[n]s[n]s[n]。
$$s[n] * \delta[n] = s[n] \tag{2.10}$$复信号的卷积
复信号 s[n]s[n]s[n] 输入到具有复冲激响应 h[n]h[n]h[n] 的系统中的卷积可以通过以 IQ 形式编写卷积来理解。它以类似的方式定义为
$$r[n] = s[n] * h[n]$$使用复数的乘法规则 I·I - Q·Q 和 Q·I + I·Q
$$I \rightarrow r_I[n] = \sum_{m=-\infty}^{\infty} s_I[m] h_I[n - m] - \sum_{m=-\infty}^{\infty} s_Q[m] h_Q[n - m]$$$$Q \uparrow r_Q[n] = \sum_{m=-\infty}^{\infty} s_Q[m] h_I[n - m] + \sum_{m=-\infty}^{\infty} s_I[m] h_Q[n - m] \tag{2.11}$$这可以写成单个实数卷积的组合。
$$I \rightarrow r_I[n] = s_I[n] * h_I[n] - s_Q[n] * h_Q[n]$$$$Q \uparrow r_Q[n] = s_Q[n] * h_I[n] + s_I[n] * h_Q[n]\tag{2.12}$$由于恒等式 cosAcosB−sinAsinB=cos(A+B)\cos A \cos B - \sin A \sin B = \cos (A + B)cosAcosB−sinAsinB=cos(A+B),I 表达式中的负号表明两个对齐轴项的相位实际上是在相加。显然,恒等式仅在可以提取幅度作为公因子的情况下适用于上述方程,但相位对齐的概念仍然成立。同样,恒等式 sinAcosB+cosAsinB=sin(A+B)\sin A \cos B + \cos A \sin B = \sin (A + B)sinAcosB+cosAsinB=sin(A+B) 表明在 Q 表达式中,两个交叉轴项的相位也在相加。因此,复卷积可以描述为一个过程:
- 计算 4 个实卷积:I∗II * II∗I,Q∗QQ * QQ∗Q,Q∗IQ * IQ∗I,以及 I∗QI * QI∗Q
- 通过相位对齐两个对齐轴卷积 (I∗I−Q∗Q)(I * I - Q * Q)(I∗I−Q∗Q) 来获得 I 分量
- 将两个交叉轴卷积 (Q∗I+I∗Q)(Q * I + I * Q)(Q∗I+I∗Q) 相加,获得 Q 分量
这些计算显示在图 2.10 中,其中双箭头表示复数操作。
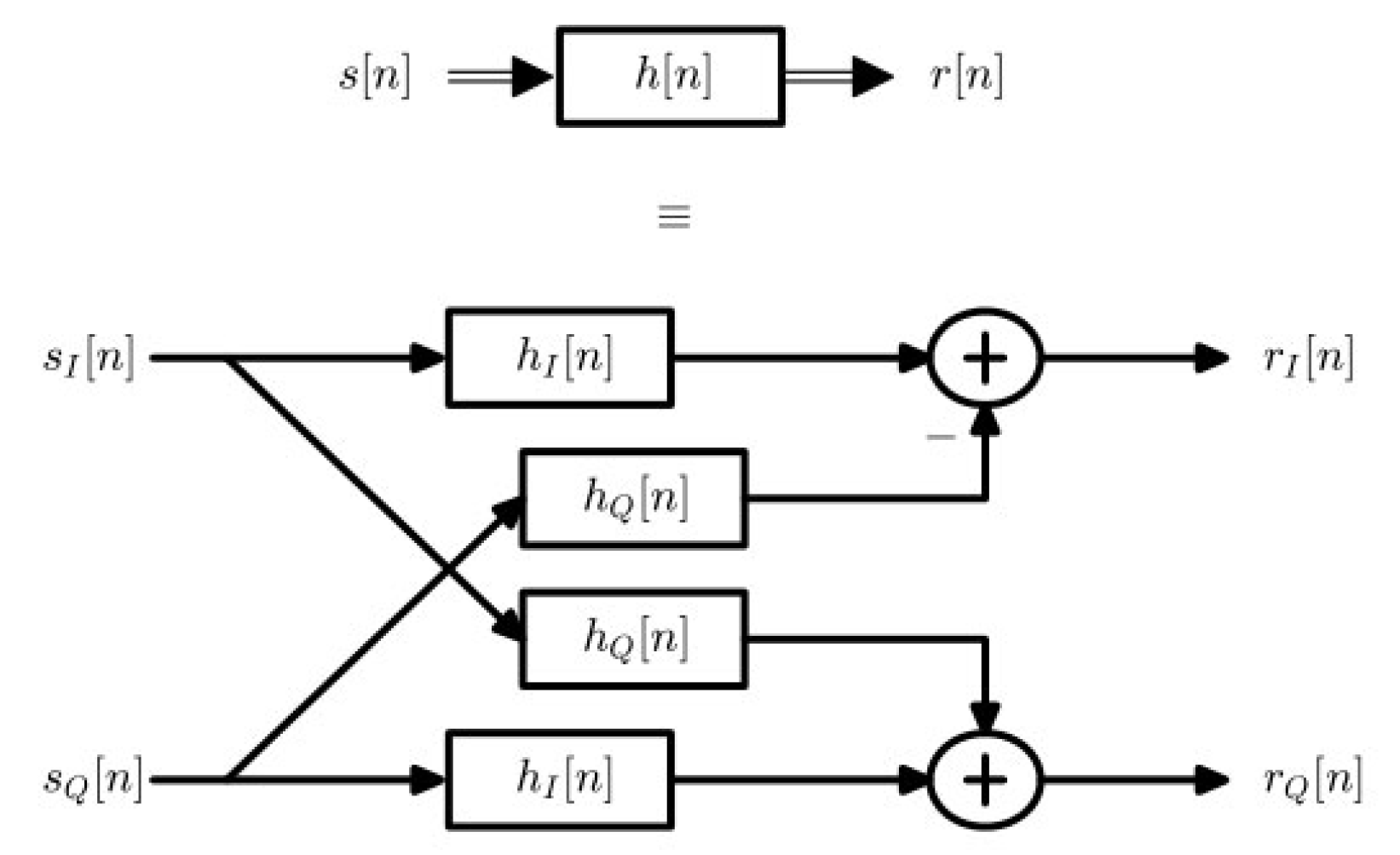
图 2.10: 两个复信号 s[n]s[n]s[n] 和 h[n]h[n]h[n] 之间的卷积
通过卷积计算相关性
回顾方程 (1.38) 中相关性的定义,如下所示:
$$\text{corr}[n] = \sum_{m=-\infty}^{+\infty} s[m] \cdot h[m-n] = \sum_{m=-\infty}^{+\infty} s[m] \cdot h[-(n-m)]$$因此,相关性可以通过卷积来定义,如下所示:
$$\text{corr}[n] = s[n] * h[-n] \tag{2.13}$$从传统方法的角度来看,两信号之间的相关性可以通过计算卷积的高效方法来实现,只不过没有信号的翻转。这是因为 h[−n]h[-n]h[−n] 翻转信号一次,而卷积再次翻转它,从而将原始信号恢复。
从直观方法的角度来看,很明显,负号与现在 −n−n−n 结合,将未来转变为过去,将过去转变为未来。因此,原始信号的最后一个样本最先到达,因为它已经变成了最远的过去。





















 4579
4579

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








