科学计算与Matlab笔记：第5章：数据分析与多项式计算（插值 拟合）

1. 数据统计分析

a. 求最大元素与最小元素

>> x=[-43,72,9,16,23,47]

x =

   -43    72     9    16    23    47

>> y=max(x)

y =

    72

>> [y,k]=max(x)

y =

    72


k =

     2

>> A=[13,-56,78;25,63,-235;78,25,563;1,0,-1]

A =

    13   -56    78
    25    63  -235
    78    25   563
     1     0    -1

>> max(A)

ans =

    78    63   563

>> max(A,[],2)

ans =

    78
    63
   563
     1

>> max(max(A))

ans =

   563

>> max(A(:))

ans =

   563

b. 求平均值与中值

c.求和与求积

d. 累加和与累乘积

>> X=[1,2,3,4,5,6,7,8,9,10];
>> y1 = prod(x)

y1 =

  -481935744

>> y2 = cumprod(X)

y2 =

  Columns 1 through 4

           1           2           6          24

  Columns 5 through 8

         120         720        5040       40320

  Columns 9 through 10

      362880     3628800

样本标准差：

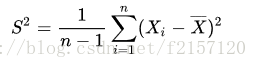
整体标准差：

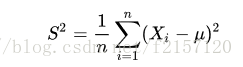
e. 求标准差与相关系数

f. 排序

2. 多项式计算

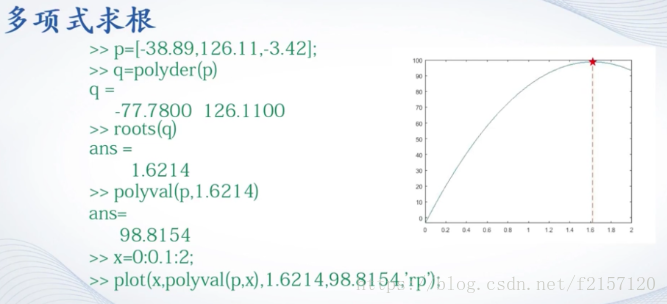
3. 数据插值

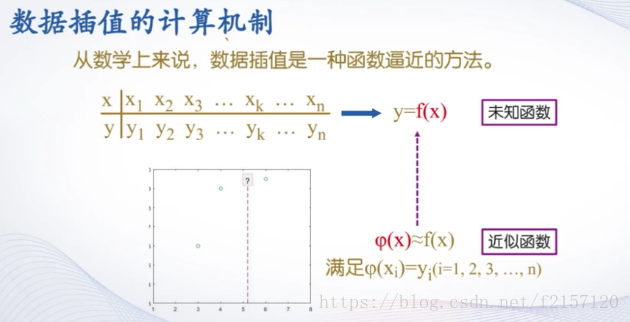
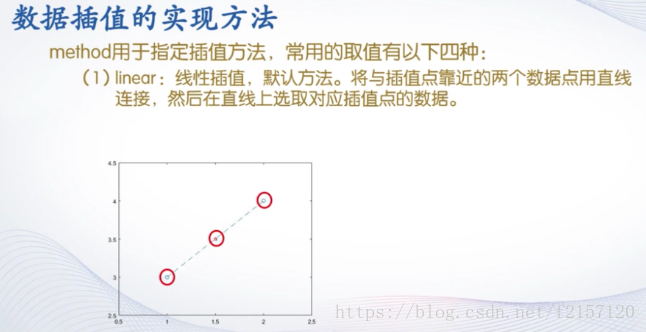
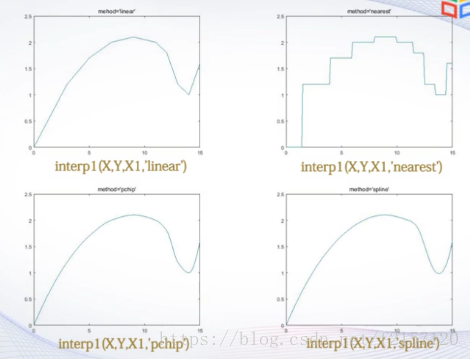
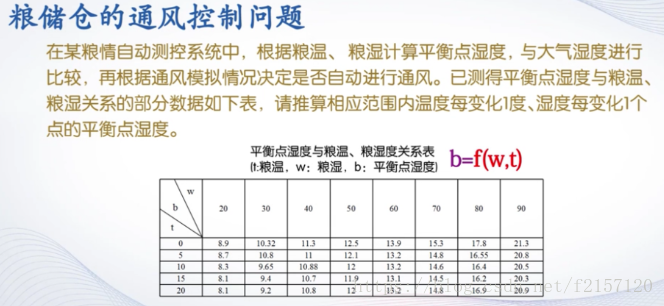
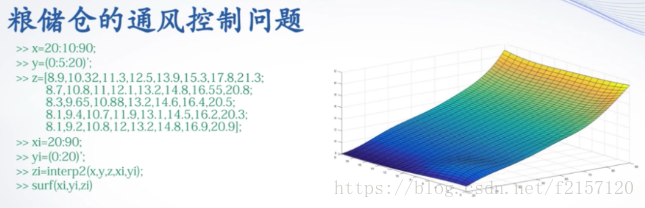
4. 数据插值应用举例

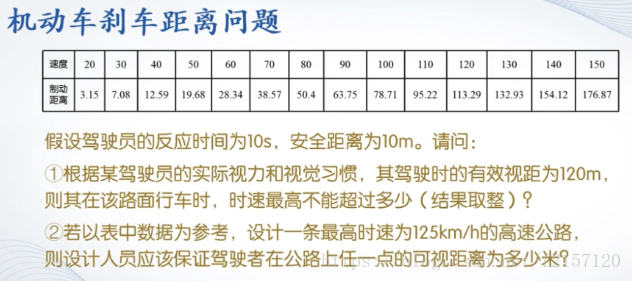
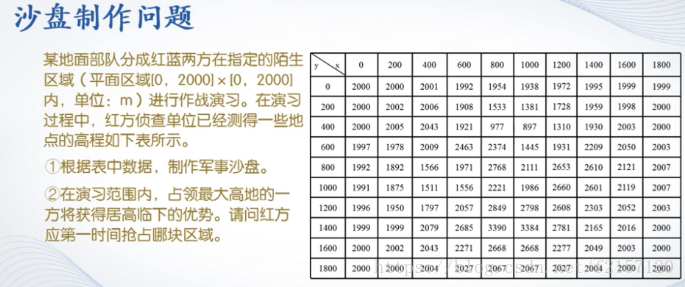
5. 曲线拟合

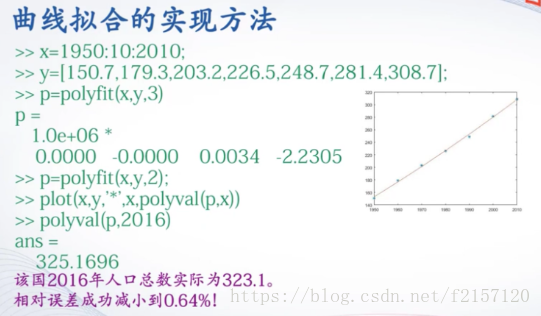
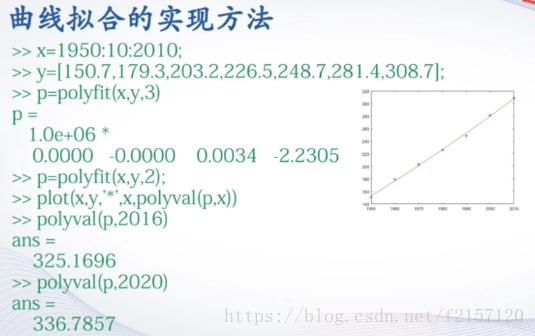
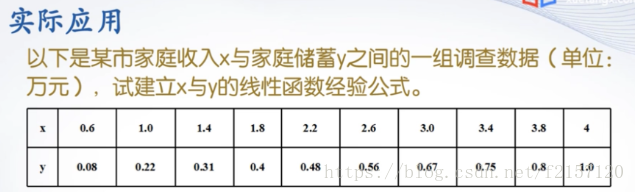
6. 曲线拟合应用举例

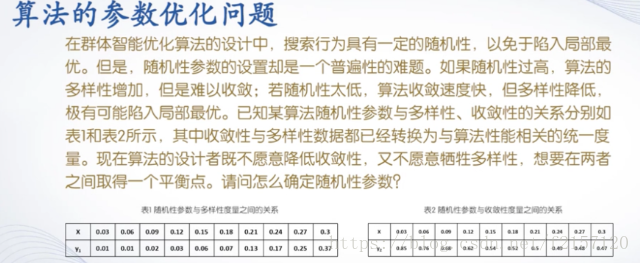
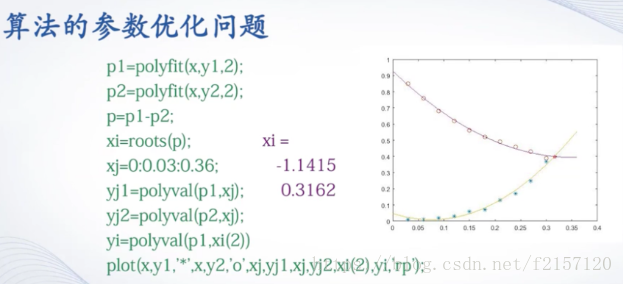
在实现方法上，数据插值要求逼近函数经过样本点，而曲线拟合不要求逼近函数经过样本点，只要求总体误差最小。

在结果上，数据插值往往分段进行逼近，没有统一的逼近函数。而曲线拟合用一个函数进行整体逼近，有确定的函数表达式。

在侧重点上，数据插值一般用于样本区间内的插值计算，而曲线拟合不仅可以估算区间内其它点的函数值，还可以预测时序数据的发展趋势，以及从统计数据中总结一般性经验。

在应用场合方面：如果样本数据为精确数据，适合采用数据插值方法，如果样本数据为统计数据或存在误差，适合采用曲线拟合的方法。