Machine Learning Techniques 笔记：2-5 Kernel Logistics Regression

上节2-4中有讲，如果SVM中允许犯一点点错误，把原来很严格的hard-margin改成soft-margin，允许违反一些些边界，用C代表惩罚，与原来形式类似，唯一的差别，就是alpha n的上界为C。

一开始的出发点：与维度无关。

LIBLINEAR，LIMSVM（专门求解dual SVM）由台大林志远老师实验室开发

把margin violation记录在kesi n这个变数里面，把有条件的最佳化问题想办法转化为对偶问题求解。

如果给定任何一个边界b，w，最终需要知道的是违反了多少的边界。

对于任何一个点，只有两种情形，有违反：则记录这个点到底距离想要的1有多远，这个数一定大于等于0

没有任何违反，kesi n记录的只实际上是0

这样，kesi n不再是变数，而是根据b，w来计算出来。

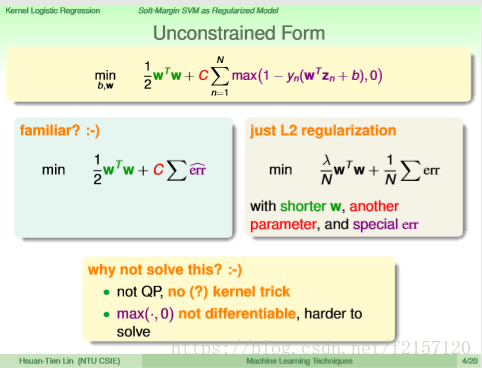
用w的长度来替代复杂度，用一个替代的error。

我们并没有直接用这个公式求解，可能会不好解

Regularization：想让Ein变小，但加上一个限制条件。

Hard margin SVM：相当于是在Ein上面再加上条件，一定要让ooxx分开，再加上更多的条件，并且希望w的长度越小越好。

Soft Margin SVM看起来与L2 Regularization看起来形式一样。

大的C，代表小的lamada，代表小的regularization

ys同号，Err = 0， ys不同号，Err = 1 - ys

soft-margin，间接的把0/1 error做好。

SVM error measure, usually called hinge error measure.

errSCE： scalled error.

两种error measure很类似

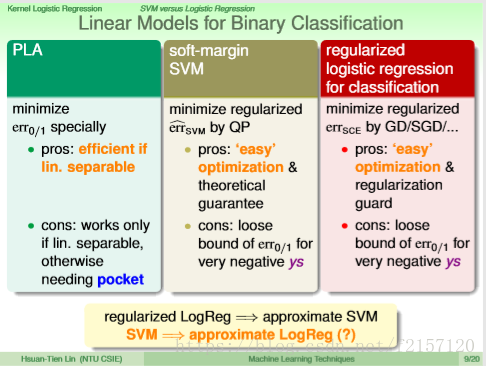
Soft margin SVM 的解可以作为logistics Regression的某个解。

regularized logistics regression，几乎是在解一个soft-margin SVM

解完SVM后，会不会也得到某个logistics regression的解呢？即会不会得到00xx的概率？

如何把SVM，用于logistics regression？

idea1：把b，w作为LR的近似开始点，这样几乎丧失了LR的特性。

idea2：把b，w作为起始点，run LR，与直接跑LR得到的结果差不多。

这两个方法看起来都有缺点。

SVM只是分开ooxx，但不具有概率的特性。Logistics Regression则具有该特性。 SVM的解作为Logistics Regression的起始点，快速求解。

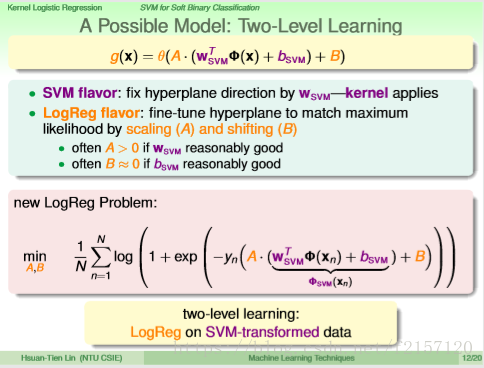
如何融合SVM与LR的特点，做出一个不一样的结果？

把SVM算出来的值（Wz+b），实际上是一个分数。如果要让这个值有SVM Flavor，则加上两个因数进行防缩，一个是A防缩因子，另一个是B，加上平移因子B做LR的训练，一般A大于0，B很接近于0

wz+b 看作是一个特殊的转换 fei（xn）

融合SVM与Logistics Regression,

SVM转换，LR做微调，最后返回g

B可以平移SVM的边界，针对LR max likelyhood做的更好

真的在Z空间里面找LR的解，怎么办？

在Z空间里面真正的做Logistics Regression， 而不是刚才的近似解。 Logistics Regression根本不是一个QP问题（二次优化）

之前的kernel trick为什么会work？如果把最佳的w看成一堆z的线性组合，则可以换成kernel来解决。

最佳的w是一堆z的线性组合。 SVM的组合系数来自于对偶问题的解，PLA组合系数来此于训练过程中z参与了多少次错误矫正，LogReg的组合系数来自于GD/SGD过程中告诉我们到底该按照多大的步数走。

如果解的是L2-regularzied linear model时，最后结果w就可以表示为z的线性组合。

w平行：可以用z线性组合的

w垂直：余下的，与w垂直的部分。

希望，最后w垂直为0.

w star：最佳解。

专心求beta即可。

Kernel LR：可否用不同的角度看它在做些什么事情？

1.可以看成是K与beta做内积，看成是n维空间，w的权重。

2. 矩阵形式，看成beta的linear model

与alpha不一样，kernel svm解出来的beta大多数不是0

Gaussian Kernel的线性组合？？？