从宽泛的概念学习到图像相关的具体内容了。从本节开始的学习,我会尽量结合代码去理解每个部分。
1、图像二值化
图像二值化是指将256阶的灰度图通过合适的阈值转化为二值图。上一篇对 阶、二值图等概念都提过了。不过这里说是256阶,感觉不必纠结是256阶还是几阶,反正是转化成只有两个值。转化成黑白,通常是用于实现将两种东西分开的目的,例如桌子上的硬币、纸上的文字等,然后在用来作为原料实现其他的功能。具体的一个简单的例子,将桌面上的硬币跟桌面分开,代码示例如下:
string path = "coin.png";
Mat coin = imread(path);
cout << coin.channels() << endl; // 发现竟然是三通道的RGB
imshow("coin", coin);
waitKey();
int height = coin.rows;
int width = coin.cols;
Mat coin_gray(height, width, CV_8UC1, Scalar(0));
for (int i = 0; i < height; i++)
{
for (int j = 0; j < width; j++)
{
Vec3b pixel = coin.at<Vec3b>(i, j);
coin_gray.at<uchar>(i, j) = pixel[0] * 0.299 + pixel[1] * 0.587 + pixel[2] * 0.114;
}
}
cout << coin_gray.channels() << endl; // 单通道
imshow("coin_gray", coin_gray);
waitKey();
Mat coin_binary(height, width, CV_8UC1, Scalar(0));
int Threshold = 80;
for (int i = 0; i < height; i++)
{
for (int j = 0; j < width; j++)
{
uchar tmp_value = coin_gray.at<uchar>(i, j);
if (tmp_value > Threshold)
coin_binary.at<uchar>(i, j) = 255;
else
coin_binary.at<uchar>(i, j) = 0;
//coin_binary.at<uchar>(i, j) = tmp_value > Threshold ? 255 : 0;
}
}
imshow("coin_binary", coin_binary);
waitKey();
写得有点啰嗦,因为先把三通道的图像转换成单通道再取阈值为80进行二值化。核心的部分其实就是将大于阈值的置为255(全白),其余置为0(全黑)。
for (int i = 0; i < height; i++)
{
for (int j = 0; j < width; j++)
{
uchar tmp_value = coin_gray.at<uchar>(i, j);
if (tmp_value > Threshold)
coin_binary.at<uchar>(i, j) = 255;
else
coin_binary.at<uchar>(i, j) = 0;
//coin_binary.at<uchar>(i, j) = tmp_value > Threshold ? 255 : 0;
}
}
效果还行,将硬币和桌子分开了:
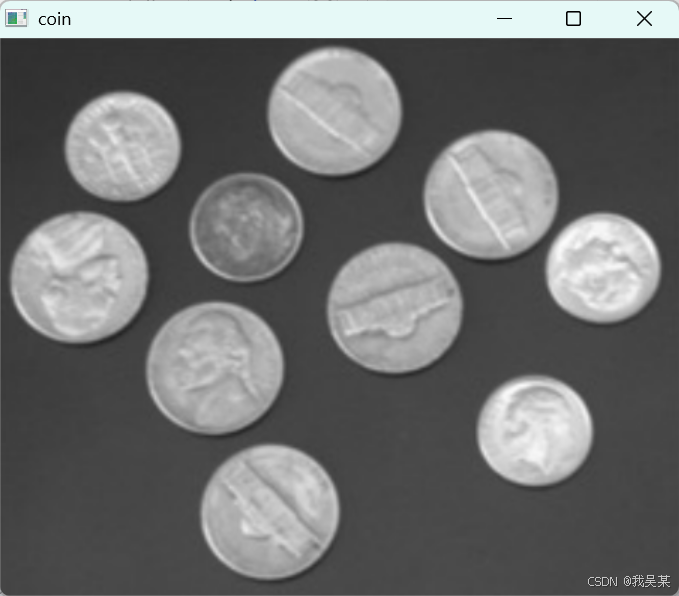


不过我后面发现上面写得有点多余,因为用imread读图片的时候,可以直接指定以灰度图像的方式来读取,也可以直接把彩色图直接转化成灰度图。
string path = "coin.png";
Mat coin = imread(path, 0); //第二个参数为0,指定以灰度图的方式读取
cout << coin.channels() << endl;
imshow("coin", coin);
waitKey();
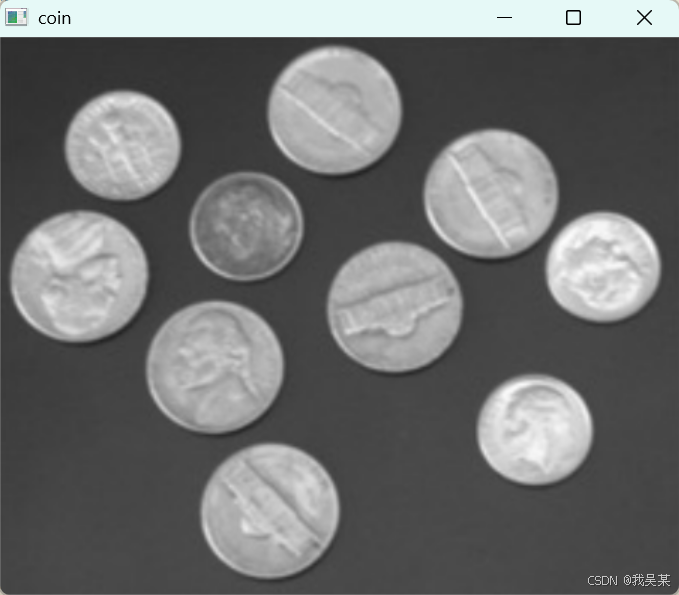

至于这个阈值,暂时是瞎猜的,取了很多个一个一个试,最后取了80,得到比较好的结果。假如多试几个阈值的话,可以看到下面的结果:
for (int Threshold = 30; Threshold <= 100; Threshold = Threshold + 10)
{
for (int i = 0; i < height; i++)
{
for (int j = 0; j < width; j++)
{
uchar tmp_value = coin_gray.at<uchar>(i, j);
if (tmp_value > Threshold)
coin_binary.at<uchar>(i, j) = 255;
else
coin_binary.at<uchar>(i, j) = 0;
}
}
string title = "coin_binary_th_" + to_string(Threshold);
imshow(title, coin_binary);
}
waitKey();

由此可以看出,选择合适的阈值是二值图效果的关键。下面的内容也基本是围绕如何找到合适的阈值来展开的。
2、全局二值化
全局二值化值的是使用单一阈值对图像进行分割。通常用于直方图上具有双峰性的图像。一般双峰之间存在交叉的部分,所以要通过阈值将前后景完全分离是不可能的,只能是寻找一个最优的阈值。
3、P-tile法
P-tile法也叫百分比阈值法,它假设已知图像中前景占整体的P%,然后依次累计灰度直方图,直到累积值大于等于预设的比例,此时的灰度级即为所求的阈值。思路比较简单,尝试用代码实现一下。
int p_tile()
{
string path = "coin.png";
Mat coin = imread(path, 0);
Mat coinHist;
int histSize = 256;
float range[] = {0, 256};
const float *histRange = {range};
calcHist(&coin, 1, 0, Mat(), coinHist, 1, &histSize, &histRange);
normalize(coinHist, coinHist, 1.0, 0, NORM_L1, -1, Mat());
/* p-tile法求阈值 */
float P_TILE = 0.66;
float sum = 0.0;
int Threshold = 0;
for (; Threshold < 256; Threshold++)
{
sum += coinHist.at<float>(Threshold);
if (sum >= P_TILE)
break;
}
/* end */
Mat displayCoin(coin.rows, coin.cols, CV_8UC1, Scalar(0, 0, 0));
for (int i = 0; i < coin.rows; i++)
{
for (int j = 0; j < coin.cols; j++)
{
uchar val = coin.at<uchar>(i, j);
if (val > Threshold)
displayCoin.at<uchar>(i, j) = 255;
else
displayCoin.at<uchar>(i, j) = 0;
}
}
imshow("coinBinary", displayCoin);
waitKey();
return 0;
}

在已知百分比为66%的情况下能计算得到一个合适的阈值。这种方法非常需要已知这个百分比,在前后颜色相差较大的时候可以通过面积的估算得到大致的百分比。很明显这种方法不太适用在一般的情况。
4、最小误判概率法
在呈现双峰的直方图中,预设一个阈值,那么可以求出误判的概率。然后再求使得误判概率最小的阈值。这部分原理的推导其实没看懂。
5、大津法(OTSU)
大津法认为最佳的阈值应该使类内方差尽可能小,类间方差尽可能大。
6、局部自适应二值化
上面介绍的是全局二值化,也就是使用一个阈值将图像分割成二值图。但是在一些场合,仅仅对全局使用一个阈值是不够的,例如纸上的字,由于光线的原因,一些字符的颜色和背景是相同的,在颜色分布上不呈现双峰性。这种时候就要将图像分割成多个子区域,这些子区域可能就呈现出双峰性了。然后对子区域分别求阈值,就能取得较好的效果。
7、opencv自带的二值化函数threshold
threshold函数可以用于固定阈值、大津法、局部自适应等方法。不过p-tile法和最小误判概率法不能用threshold。下面详细介绍threshold的用法中固定阈值的部分。
threshold(coin, coin_dst, 80, 255, THRESH_BINARY);
//THRESH_BINARY 二进制阈值,超过阈值80时置为255,反之置为0
threshold(coin, coin_dst, 80, 255, THRESH_BINARY_INV);
//THRESH_BINARY_INV 反二进制阈值,超过阈值80时置为0,反之置为255
threshold(coin, coin_dst, 80, 255, THRESH_TRUNC);
//THRESH_TRUNC 截断阈值,超过阈值80时置为阈值,反之不变
threshold(coin, coin_dst, 80, 255, THRESH_TOZERO);
//THRESH_TOZERO 阈值化为0,超过阈值时不变,反之置为0
threshold(coin, coin_dst, 80, 255, THRESH_TOZERO_INV);
//THRESH_TOZERO_INV 反阈值化为0,超过阈值时置为0,反之不变
上面几个用法是根据最后一个参数的类型决定超过阈值以及小于阈值时的行为的。而大津法THRESH_OTSU则可以自动确定阈值,经常和THRESH_BINARY 以及THRESH_BINARY_INV结合使用。
threshold(coin, coin_dst, 80, 255, THRESH_BINARY | THRESH_OTSU);
大津法中,第三个参数阈值就不会被使用到了。不过要说效果嘛,可能其实有些时候并没有指定阈值的效果那么好。

8、opencv自带的二值化函数adaptiveThreshold
adpativeThreshold函数用于局部自适应二值化,在单个阈值不足以分割图像时使用。
adaptiveThreshold(coin, coin_dst, 255, ADAPTIVE_THRESH_GAUSSIAN_C, THRESH_BINARY, 15, 5);
前三个参数跟threshold意思是一样的,第四个是自适应阈值算法,第五个是二进制阈值或反二进制阈值,第六个是局部尺寸的区域,第七个则是自适应阈值算法结果需要需要减去的常数。
参数四为ADAPTIVE_THRESH_GAUSSIAN_C时表示是局部邻域块的加权和,为ADAPTIVE_SHRESH_MEAN_C时则是局部邻域块的平均值。


具体使用的时候发现,效果跟全局二值化相比自然是好很多,但是具体的效果也需要通过调整窗口大小和常数来取得最好的结果。
9、连通域标记
通过二值化将前后景分开之后,由于前景的物体可能存在重叠的情况,例如硬币之间可能存在重叠的情况,此时其实还不能够直接计算得到硬币的数量,还涉及到形态学部分的内容。这一部分的内容在后面会详细介绍(应该会吧,还没往后看)。此时讨论一下没有重叠的情况下的自动计数。为了方便查看,使用的例子是二值化的结果。
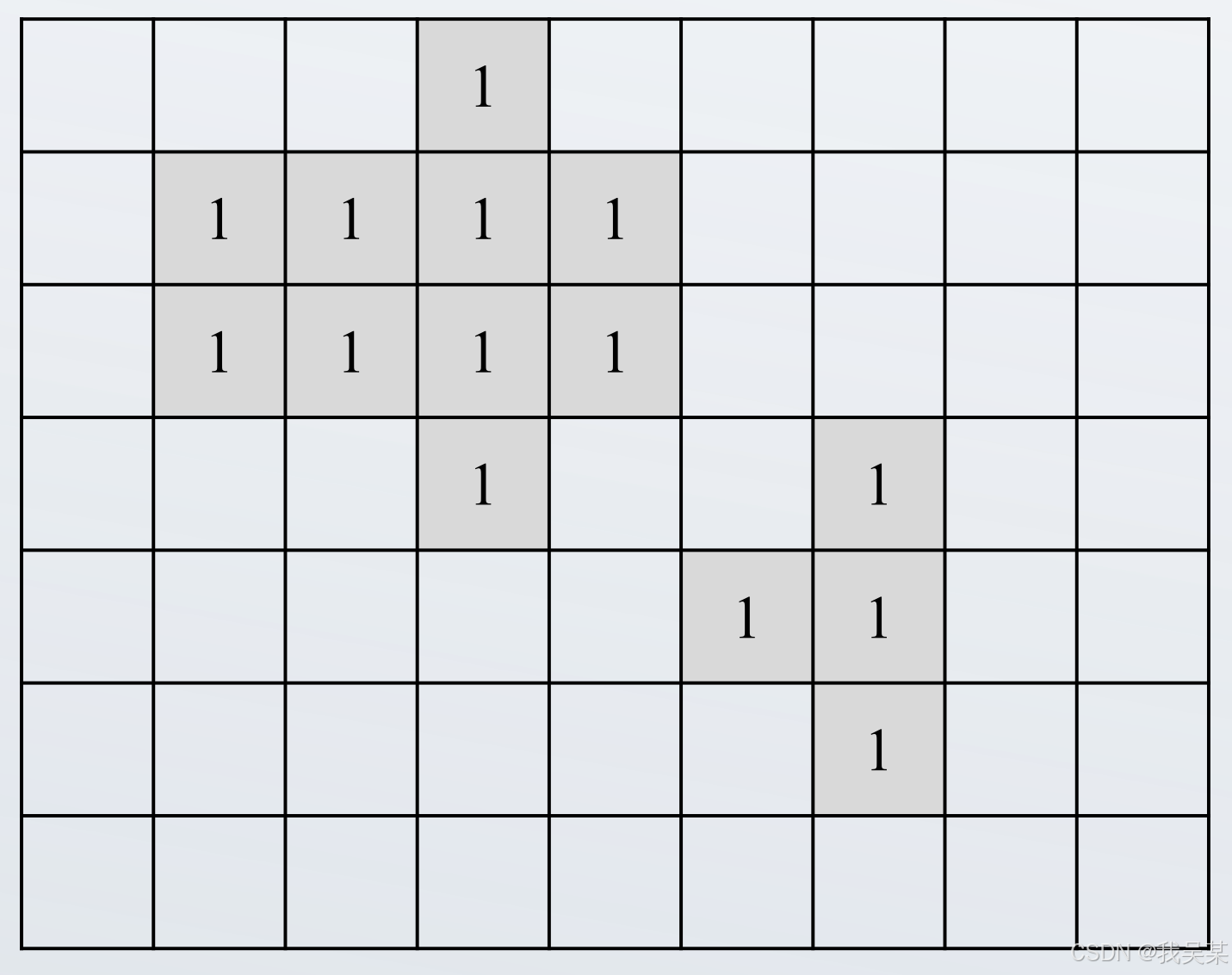
(1)、种子填充法Seed Filling
第一种方法称为种子填充法,遍历图像,到某个前景像素点时给它一个标签,然后对这个像素邻接的前景像素全都给一个相同的标签,视作同一个硬币。遍历结束后即可得到标签的数量,即硬币的数量。代码的实现如下:
int getSeedCounts(Mat &img)
{
int seedCounts = 0;
int height = img.rows;
int width = img.cols;
vector<vector<bool>> visited(height, vector<bool>(width, false));
queue<int> que;
int next_x[] = {-1, 1, 0, 0};
int next_y[] = {0, 0, -1, 1};
for (int i = 0; i < img.rows; i++)
{
for (int j = 0; j < img.cols; j++)
{
if (img.at<uchar>(i, j) == 255 && visited[i][j] == false)
{
visited[i][j] = true;
que.push(i);
que.push(j);
seedCounts++;
}
while (!que.empty())
{
int index_x = que.front();
que.pop();
int index_y = que.front();
que.pop();
for (int k = 0; k < 4; k++)
{
int tmp_x = index_x + next_x[k];
int tmp_y = index_y + next_y[k];
if (tmp_x < 0 || tmp_x >= img.rows || tmp_y < 0 || tmp_y >= img.cols)
continue;
if (img.at<uchar>(tmp_x, tmp_y) == 255 && visited[tmp_x][tmp_y] == false)
{
visited[tmp_x][tmp_y] = true;
que.push(tmp_x);
que.push(tmp_y);
}
}
}
}
}
return seedCounts;
}
基本的思路就是遍历图像,找到还没访问到的前景像素点之后将它加入到队列里面,然后对这个像素的邻接前景像素加入队列,依次进行下去,最后就把这个硬币的所有像素点都打上了已访问的标记,此时就找到一个硬币了,接着继续,直到结束就找到所有硬币并计数完成了。对于例子中取阈值为80的二值图中的硬币数量,最后的结果是10,符合预期的效果。这个算法其实就是简单的广度优先算法,在刷leetcode的时候就会经常遇到。不过这只是我对于种子填充法的理解,具体是不是就不知道了。
(2)、等价表法Two-Pass
第二种方法是等价表法。第一次遍历图像时,给前景像素点添加标记,并维护一个等价表。此时当前景像素的四邻接像素没有标记时,则添加新的标记,有一个则添加相同的标记,存在多个则取最小的并维护等价表。说是四邻接关系,但是因为是遍历,所以其实只判断左边的像素和上面的像素。第二次遍历时,根据等价表更新标记。代码的实现如下:
int TwoPass(const Mat &img)
{
Mat labels = Mat::zeros(img.size(), CV_32SC1);
vector<int> parent(1, 0);
int next_label = 1;
for (int y = 0; y < img.rows; y++)
{
for (int x = 0; x < img.cols; x++)
{
if (img.at<uchar>(y, x) != 255)
continue;
int left = (x > 0) ? labels.at<int>(y, x - 1) : 0;
int up = (y > 0) ? labels.at<int>(y - 1, x) : 0;
if (left == 0 && up == 0)
{
labels.at<int>(y, x) = next_label;
parent.push_back(next_label); // parent[next_label] = next_label
next_label++;
}
else if (left != 0 && up != 0)
{
int min_label = min(left, up);
int max_label = max(left, up);
labels.at<int>(y, x) = min_label;
parent[max_label] = min_label;
}
else
{
labels.at<int>(y, x) = max(left, up);
}
}
}
for (int y = 0; y < labels.rows; y++)
{
for (int x = 0; x < labels.cols; x++)
{
int label = labels.at<int>(y, x);
if (label == 0)
continue;
labels.at<int>(y, x) = parent[label];
}
}
int num_components = 0;
for (int i = 1; i < next_label; i++)
{
if (parent[i] == i)
{
num_components++;
}
}
return num_components;
}
第一遍扫描时,对于一个前景像素点,得到它上面和左边像素点的标签,如果都是0说明没有标签,那么他就是新的标签;如果都不是0则取最小的值,并维护等价表;如果只有一个不是0,那么直接取这个值。第二次扫描时,对前景像素点,根据等价表更新标签值。最后对等价表中值与下标相同的表示是根标签,计数即得到前景硬币的数量。最后的结果跟种子填充法的结果相同。
10、OpenCV的连通域标记函数connectedComponentsWithSatas
Opencv有自带的连通域标记函数connectedComponentsWithSatas,可以对二值图进行连通域标记,同时返回连通域的状态和中心坐标。
string path = "coin.png";
Mat coin = imread(path, 0);
Mat coin_dst;
threshold(coin, coin_dst, 80, 255, THRESH_BINARY);
Mat labels, stats, centroids;
int num_components = connectedComponentsWithStats(coin_dst, labels, stats, centroids, 8);
1、二值图
2、标签化的结果,类型是32位无符号整型单通道,因为标签数量可能uchar不够存
3、状态矩阵,连通域数量x5,分别是最小外接矩形左上角坐标、宽、高、面积。第一行是背景
4、连通域中心矩阵,连通域数量x2,表示连通域中心坐标。第一行是背景
返回值是标签数量,包括背景,背景的标签是0
如果用得到的状态矩阵把最小外接矩形画出来就可以看到每个连通域,代码示例:
int test()
{
string path = "coin.png";
Mat coin = imread(path, 0);
Mat coin_dst;
threshold(coin, coin_dst, 80, 255, THRESH_BINARY);
Mat labels, stats, centroids;
int num_components = connectedComponentsWithStats(coin_dst, labels, stats, centroids, 8);
Mat coin_color;
cvtColor(coin, coin_color, COLOR_GRAY2BGR);// 灰度图转化为彩色
for (int i = 1; i < num_components; i++) // 跳过背景(i=0)
{
int x = stats.at<int>(i, CC_STAT_LEFT);
int y = stats.at<int>(i, CC_STAT_TOP);
int w = stats.at<int>(i, CC_STAT_WIDTH);
int h = stats.at<int>(i, CC_STAT_HEIGHT);
rectangle(coin_color, Point(x, y), Point(x + w, y + h), Scalar(0, 255, 0), 1);
}
imshow("coin", coin_color);
waitKey();
return 0;
}

效果还不错。这里提一下我绘图过程出现的问题。我尝试往灰度图中使用彩色画矩形,结果似乎出现显示和位置上的问题。使用cvtColor之后转化为彩色图才出现满意的效果。
还有个connectedComponents函数,也是用于计算连通域的,不过它没有其他统计信息。
11、如何调用本机的摄像头
int useVideoCapture()
{
VideoCapture cap;
cap.open(0);
if (!cap.isOpened())
{
return -1;
}
namedWindow("Capture Feed", WINDOW_AUTOSIZE);
while (true)
{
Mat frame;
cap >> frame;
if (frame.empty())
{
break;
}
imshow("Capture Feed", frame);
if (waitKey(1) == 27)
break;
}
cap.release();
destroyAllWindows();
return 0;
}
OpenCV调用摄像头比较简单,使用VideoCapture类定义一个对象,然后打开默认摄像头,cap.open(0)表示笔记本电脑的默认摄像头。其他设备号则表示其他摄像头。然后在死循环中,通过cap >> frame将视频的一帧输入到frame中。这里应该是VideoCapture重载了输入流运算符,从设备驱动对应的缓冲区中取出当前的一帧输入到Mat对象中,然后就可以像一张图片一样处理了。waitKey是等待按键事件并返回按键事件,参数则是等待的毫秒数。这里是按下ESC之后推出。使用完之后要release。效果就是看到了摄像头的内容。

我的笔记本电脑放在桌子下面,所以是这样的效果。
这只是关于VideoCapture类的一个简单的使用,更多的内容,后面如果有提到再仔细学习一下。
至此,本次关于图像二值化的内容就学习完毕了。本次主要学习了二值化和连通域标记的方法,最后还介绍了使用摄像头的方法。一些地方由于个人能力的限制就没详细解释。本次内容和图形绘制的内容是交替完成的,所以可能有点混乱。
 OpenCV图像二值化及连通域标记学习
OpenCV图像二值化及连通域标记学习





















 1693
1693

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








