opencv学习4：OpenCV绘图功能

原创 已于 2025-03-24 23:14:52 修改 · 1.6k 阅读 · 33 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#opencv #学习 #计算机视觉 #c++

于 2025-03-24 20:47:17 首次发布

在学习图像二值化的时候，里面涉及到直方图，我发现我对直方图这个概念能理解，但是却想不到自己要怎么去画一个直方图出来。因此，先学习一下OpenCV的绘图功能，希望达到能够将直方图绘制出来的效果。

1、绘制直线

opencv有实现在图像中增加一条直线的函数line。使用的方法很简单，传入所需的参数之后就能够在已有图像的基础上增加一条直线。其实就是在Mat中改变直线经过的像素点的颜色。具体使用方法如下：

Mat displayMat = Mat::zeros(500, 500, CV_8UC3);
line(displayMat, Point(100, 100), Point(200, 200), Scalar(0, 0, 200), 3, 4);
imshow("line", displayMat);
waitKey();

上面line函数的意思是 在displayMat这个Mat之中，或者说这个图像中，增加一条直线，直线的起点是（100，100），终点是（200， 200），其实核心就是两点确定一条直线。颜色是（0，0，200），宽度是3，邻接方式是4邻接。

上面的displayMat在这里是使用Mat的全局函数zero定义的一个全零图像，其实就是全黑图像。Point则是一个点的概念，这个不难理解。这里指定的颜色看起来是RGB的顺序，其实是BGR的顺序，这里是因为opencv最初是考虑到跟现有的一些库的兼容，然后才形成这样一种反直觉的顺序。宽度就不用多说了，最后的邻接关系则是跟之前提到的像素空间关系是同一个概念。具体来说八邻接关系跟四邻接相比，要更平滑，锯齿要更少，不过我暂时没能找到合适的例子来说明这一点，可能对于圆或者椭圆来说就能看出明显区别了。还有一种邻接关系LINE_AA，它的抗锯齿能力更强，不过看起来有点粗。

上图从左到右依次是四、八、LINE_AA三种邻接关系。 

正常来说，多条之前存在交叉关系的话，应该是后绘制的呈现出在上方的效果，具体下面看一下效果：

line(displayMat, Point(100, 100), Point(200, 200), Scalar(0, 0, 200), 3, 4);
line(displayMat, Point(200, 100), Point(100, 200), Scalar(0, 200, 0), 3, 8);

如预期所料，呈现出后绘制处于上方的效果。

除了上面的内容之外，还有最后一个参数shift，表示偏移量。

line(displayMat, Point(400, 400), Point(500, 500), Scalar(0, 0, 200), 3, 4);
line(displayMat, Point(400, 400), Point(500, 500), Scalar(0, 0, 200), 3, 4, 1);
line(displayMat, Point(400, 400), Point(500, 500), Scalar(0, 0, 200), 3, 4, 2);

具体效果就是，当偏移量为1时会发现图像上每一个点的横坐标纵坐标都变成原来1/2的效果，偏移量为2则是1/4的效果，以此类推。其余的图形的绘制跟上面的格式几乎是一样的，后面跟上面相关的概念就不赘述了。

 2、绘制矩形

绘制矩形使用的函数是rectangle，具体效果如下：

Mat displayMat = Mat::zeros(500, 500, CV_8UC3);
rectangle(displayMat, Point(100, 100), Point(200, 200), Scalar(255, 0, 0), 3, 4);
imshow("rectangle", displayMat);
waitKey();

在使用上跟绘制直线是一致的，直线的核心是两点确定一条直线，矩形的核心就是两点确定的对角线确定矩形。跟直线不同的地方就是，矩形的宽度可以是-1，表示实心矩形，效果如下：

rectangle(displayMat, Point(100, 100), Point(200, 200), Scalar(255, 0, 0), 3, 4);
rectangle(displayMat, Point(300, 100), Point(400, 200), Scalar(255, 0, 0), -1, 4);

3、绘制圆形

圆形的绘制使用的是circle，核心就是圆心和半径，其余参数都是类似的。

circle(displayMat, Point(300, 100), 25, Scalar(0, 200, 200), -1, 4);
circle(displayMat, Point(300, 200), 50, Scalar(0, 200, 0), -1, 4, 1);

4、绘制椭圆

椭圆跟圆相比就比较复杂了，它基本的核心是中心点、长短轴，因为椭圆旋转之后也是新的样子，所以椭圆的倾斜角也是核心点，除此之外，还允许指定椭圆绘制的范围，也就是说允许指定从哪个角度画到哪个角度。因此椭圆的核心有中心点、长短轴、旋转角、起始角度、结束角度五个关键要素。

ellipse(displayMat, Point(150, 150), Size(80, 40), 0, 30, 360, Scalar(0, 0, 200), 1, 4);
ellipse(displayMat, Point(300, 300), Size(80, 40), 0, 120, 360, Scalar(0, 0, 200), 1, 4);
ellipse(displayMat, Point(450, 450), Size(80, 40), 60, 120, 360, Scalar(0, 0, 200), 1, 4);

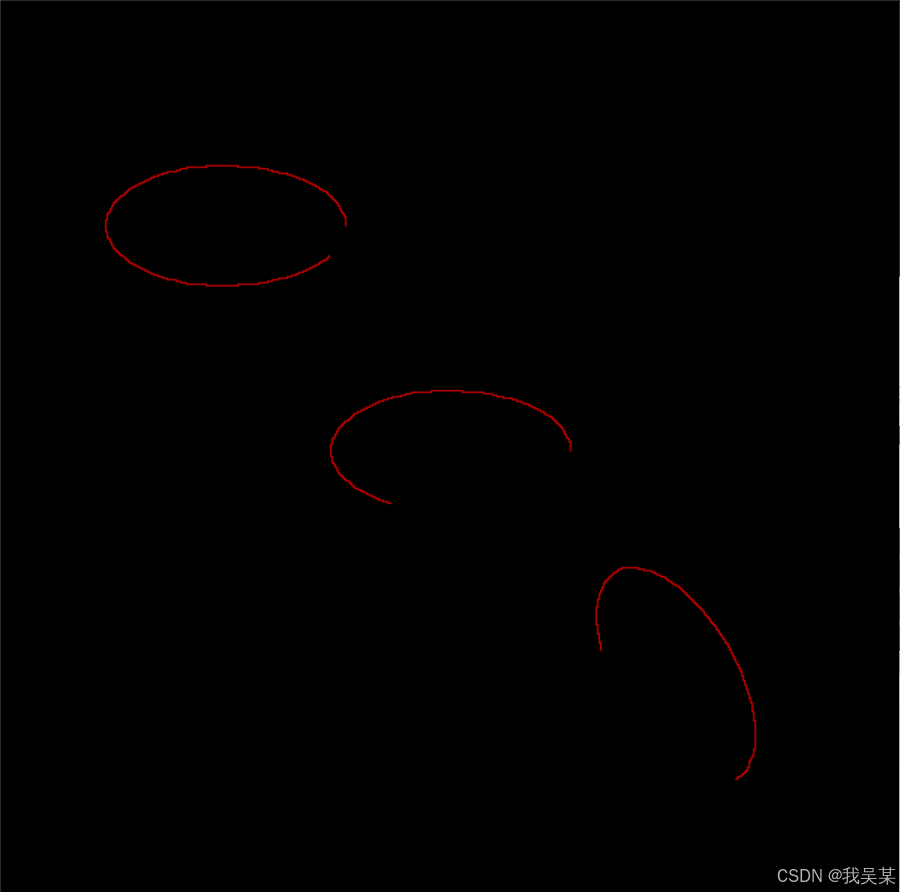
可以把圆当成特殊的椭圆，那么就可以用ellipse画圆，然后也可以指定起始角度和结束角度，画出有缺损的圆。好像吃豆人哦。

ellipse(displayMat, Point(150, 150), Size(80, 80), 0, 30, 360, Scalar(0, 0, 200), 1, 4);
ellipse(displayMat, Point(300, 300), Size(80, 80), 0, 30, 360, Scalar(0, 0, 200), -1, 4);

5、绘制特殊图案

drawMarker可以绘制的特殊图案，按照枚举值依次是加号、叉、星、方片、方块、三角、倒三角。核心的内容则是图案中心、图案类型、图案大小。

drawMarker(displayMat, Point(100, 50), Scalar(0, 255, 255), 0, 20, 1, 8);
drawMarker(displayMat, Point(100, 250), Scalar(0, 255, 255), 1, 20, 1, 8);

6、绘制文字

putText可以绘制英文字符串，核心要素就是字符串、文字位置（左下角位置）、字体类型、字体大小。具体字体有哪些不重要，需要再查一下就好。

putText(displayMat, "xiaohuang", Point(000, 30), FONT_HERSHEY_DUPLEX, 1.2, Scalar(200, 200, 0), 2, 4);

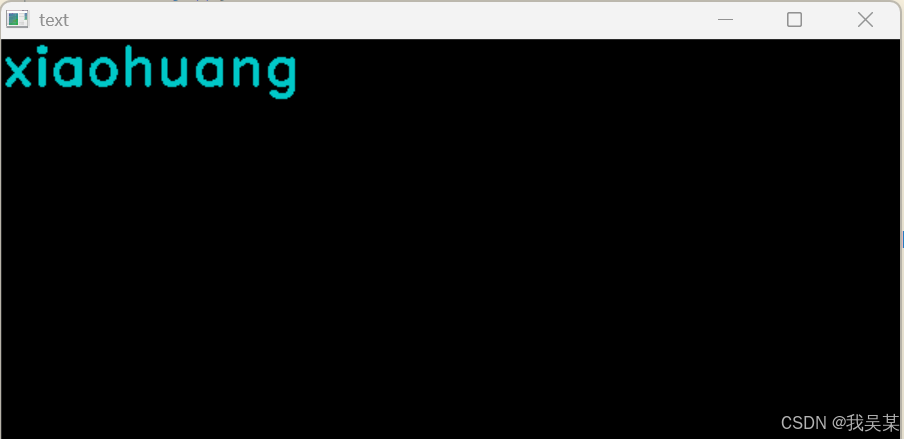
至此，几种常见的opencv绘制图形的方法介绍完毕。整体下来发现其实就是每种图形有自己的核心要素，其余参数都是一致的。

7、介绍一下其他相关的内容

目前为止，显示图像使用的都是imshow，这样的效果就是指定图像名称和图像内容，然后显示再一个窗口上。这个窗口只是默认的窗口，不允许调整窗口大小，全屏的时候则是其余部分会填充为默认的颜色。

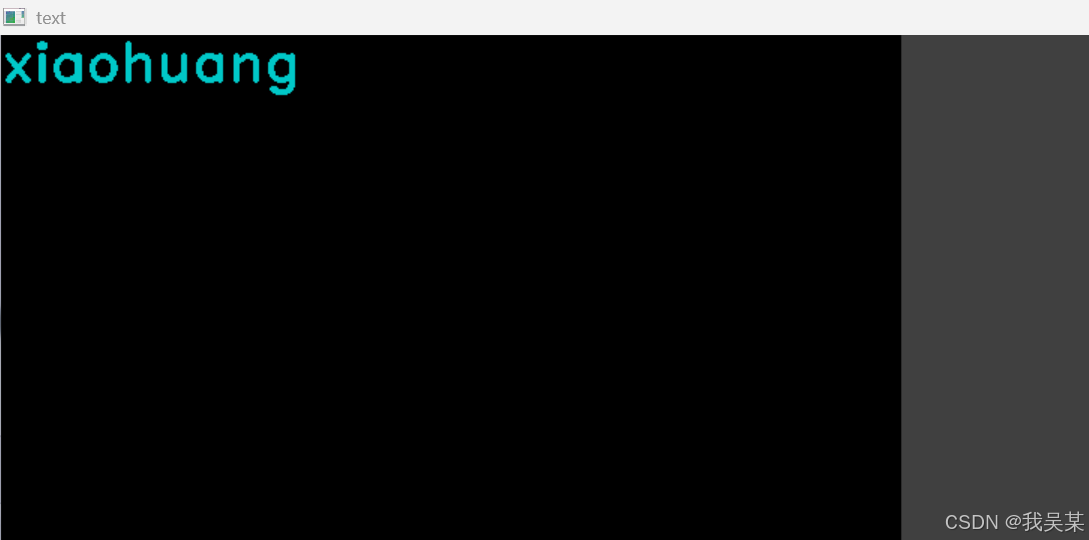
这样子就非常简陋了。下面介绍新的写法，先使用namesWindow，设置一个窗口的名称对其设置窗口的属性。后续使用imshow时，如果窗口名跟namesWindow相同则会使用设定好的样式。如下，窗口打开之后我把它变成扁的了。不过我实际发现要么不能拉伸，要么拉伸之后下一次打开会保留拉伸后的样子。按我的习惯选择使用resizeWindow来设置每次打开的初始尺寸，然后就是每次打开都是原始尺寸，然后可拉伸。

namedWindow("coin", WINDOW_NORMAL | WINDOW_KEEPRATIO);
resizeWindow("coin", image.cols, image.rows);

8、直方图的绘制（自己实现）

先理清一下思路，直方图就是像素值和像素频率构成的点连成的曲线。这里的曲线可以用多个点依次连接而成。思路清晰之后，开始尝试。

首先是要得到各个像素值的点的个数。得到个数之后还不行，因为要得到频率，所以还需要得到占总数的百分比。然后虽然说绘图需要的点的纵坐标是频率，但是绘制上去的其实还是占直方图高度的百分比，因此还需要根据预计直方图的高度得到在直方图上的纵坐标。得到纵坐标的过程中还需要考虑到纵轴跟数学上的纵轴是方向相反的，因此还需要做一下数值的变换。最后再加一点点偏移，一个自己实现的直方图就出现了。

int drawHist()
{
    string path = "coin.png";
    Mat coin = imread(path, 0);

    vector<double> counts(256, 0.0);

    int histMat_height = 400;
    int histMat_width = 600;

    int hist_height = 300;
    int hist_width = 500;

    int height = coin.rows;
    int width = coin.cols;
    int total_count = height * width;
    for (int i = 0; i < height; i++)
    {
        for (int j = 0; j < width; j++)
        {
            uchar val = coin.at<uchar>(i, j);
            counts[val] += 1;
        }
    }
    double countsMax = 0;
    for (int i = 0; i < 256; i++)
    {
        counts[i] = counts[i] / total_count;
        countsMax = max(countsMax, counts[i]);
    }

    Mat hist(histMat_height, histMat_width, CV_8UC3, Scalar(255, 255, 255));

    for (int i = 1; i < 256; i++)
    {
        line(hist, 
        Point(i * 2 + 20, histMat_height - counts[i - 1] / countsMax * hist_height - 50), 
        Point(i * 2 + 1 + 20, histMat_height - counts[i] / countsMax * hist_height - 50),         
        Scalar(0, 0, 200), 
        1, 
        4);
    }

    namedWindow("coin", cv::WINDOW_NORMAL | cv::WINDOW_KEEPRATIO);
    resizeWindow("coin", coin.cols, coin.rows);
    namedWindow("hist", cv::WINDOW_NORMAL | cv::WINDOW_KEEPRATIO);
    resizeWindow("hist", hist.cols, hist.rows);

    imshow("coin", coin);
    imshow("hist", hist);

    waitKey();

    destroyAllWindows();
    return 0;
}

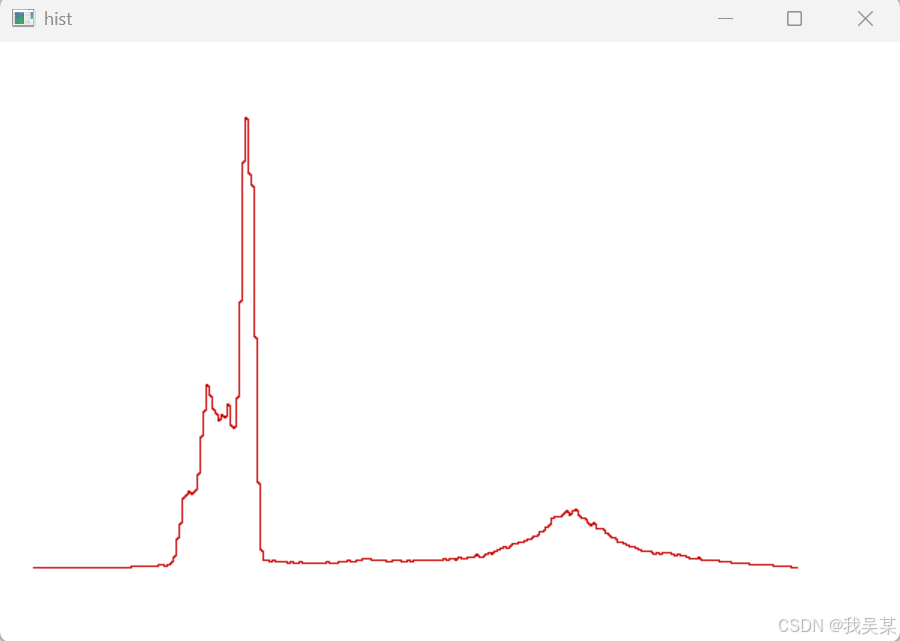
效果倒是跟预期的一样，不过确实非常粗糙。做完直方图之后再理清一下思路，主要分成三个部分，计算数量、归一化、绘制。计算频率简单，遍历之后累加。归一化简单，求每个像素值占的百分比。绘制也简单，使用line函数，带入得到的各个参数就搞定了。不过这几个步骤在opencv之中也有函数可以直接使用。

9、直方图的绘制（opencv实现）

下面依次介绍opencv绘制直方图过程中计算直方图和归一化使用的函数，calcHist和normalize。

(1)计算直方图calcHist
calcHist(&image, 1, 0, Mat(), hist, 1, &histSize, &histRange, true, false);
//原图地址
//原图数量
//需计算的通道索引
//掩码
//输出的直方图
//输出的直方图的数量
//每个维度的区间数
//每个维度的像素值区间范围
//是否均匀分布
//是否累计分布

看得出来，非常复杂。复杂主要是因为calcHist允许同时计算多张图像，因此第一个参数是原图的地址，而不是原图，然后在第二个参数上指定数量。

第三个参数则是需计算的通道索引，因为可能是彩色的图像，所以需要指定对哪个通道进行计算，值为0时代表是灰度图像。

第四个参数不想看。第五个参数则是输出的图像（Mat对象）。第六个参数则是输出的直方图的维度，一般是1。

第七个参数是每个维度的区间数，第八个则是每个维度的像素值区间范围。

第九个参数是是否均匀分布，因为直方图是允许出现范围内的值累计显示的，所以需要指定是否均匀分布。如果不均匀分布，那么第七和第八则是要分成几个区间以及每个区间的范围。

第十个参数是是否累计。累计的话会出现多张图的结果合并到一个结果的效果。

学完了还是觉得很复杂，不过对于常用的功能就只要记住下面的就可以了。其他无所谓，本来就不可能指望学一次全部记住，需要的时候知道可以这样做就可以了。这样之后，得到的hist实际上的核心数据是1*256的二维数组（只有一行的二维数组）。

Mat image = imread("coin.png", 0);
int histSize = 256;
float range[] = {0, 256};
const float *histRange = {range};
Mat hist;
calcHist(&image, 1, 0, Mat(), hist, 1, &histSize, &histRange);
(2)归一化normalize
normalize(hist, hist, 0, histImage.rows, NORM_MINMAX, -1, Mat());

这部分比较简单，至少对目前要做直方图来说比较简单。参数分别是原图、目的、最小值、最大值、类型、数据类型、掩码。类型为NORM_MINMAX会把值放缩到最小值和最大值的范围。如果是要得到频率的话就把归一化类型设为NORM_L1，最小值和最大值设为1.0，0，表示总和为1。不过如果是要绘制直方图，可以直接NORM_MINMAX，把最大值定在绘制图像的高度。数据类型-1表示输出类型跟输入一样。不考虑它的其它功能的话，他还是相等简单的。

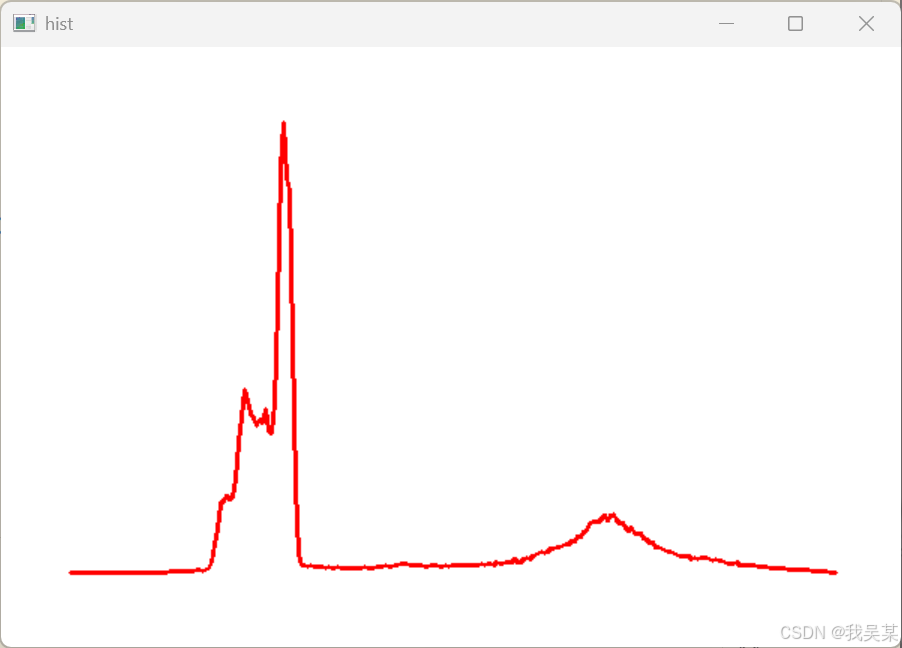
(3)绘制灰度图的直方图

 使用opencv自带的函数实现的直方图如下：

int drawHist_opencv_gray()
{
    string path = "coin.png";
    Mat coin = imread(path, 0);
    int histSize = 256;
    float range[] = {0, 256};
    const float *histRange = {range};
    Mat hist;
    calcHist(&coin, 1, 0, Mat(), hist, 1, &histSize, &histRange, true, false);

    normalize(hist, hist, 0, 1, NORM_MINMAX, -1, Mat());

    Mat histMat(400, 600, CV_8UC3, Scalar(255, 255, 255));

    for (int i = 1; i < histSize; i++)
    {
        line(histMat,
             Point(44 + i * 2, 400 - hist.at<float>(i - 1) * 300 - 50),
             Point(46 + i * 2, 400 - hist.at<float>(i) * 300 - 50),
             Scalar(0, 0, 255),
             2,
             8,
             0);
    }

    namedWindow("hist", WINDOW_NORMAL | WINDOW_KEEPRATIO);
    resizeWindow("hist", 600, 400);
    imshow("hist", histMat);
    waitKey();

    return 0;
}

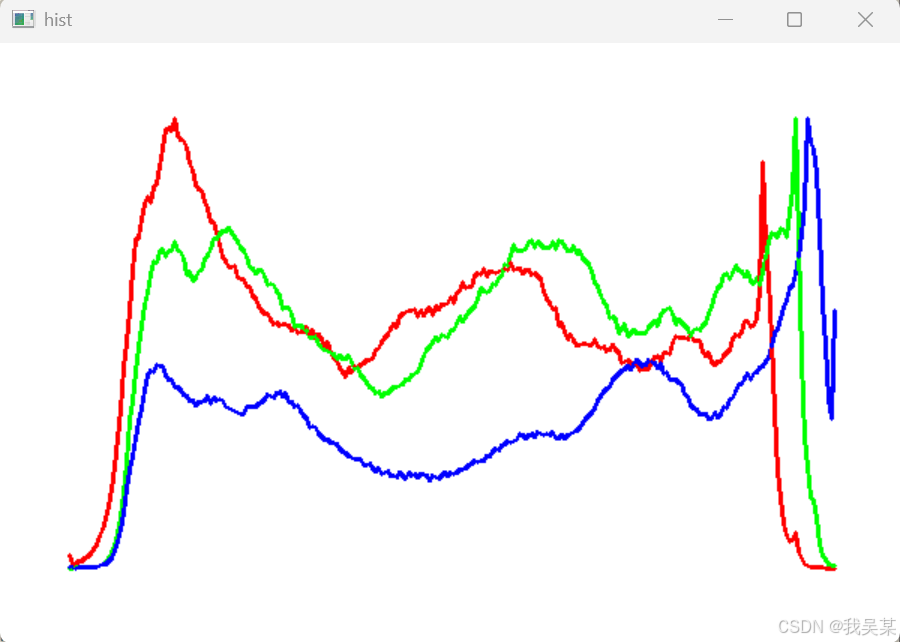
(4)绘制彩色图的直方图

跟灰度图的直方图绘制相比，彩色图几乎是将同一个过程重复三遍就可以了。然后这里可以直接用split将彩色图按通道分开。

string path = "xiaohuang.jpg";
Mat xiaohuang = imread(path);

Mat RGB[3];
split(xiaohuang, RGB);

之后就灰度图的过程重复进行。

int drawHist_opencv_color()
{
    string path = "xiaohuang.jpg";
    Mat xiaohuang = imread(path);

    Mat RGB[3];
    split(xiaohuang, RGB);

    int histSize = 256;
    float range[] = {0, 256};
    const float *histRange = {range};
    Mat hist[3];

    calcHist(&RGB[0], 1, 0, Mat(), hist[0], 1, &histSize, &histRange, true, false);
    calcHist(&RGB[1], 1, 0, Mat(), hist[1], 1, &histSize, &histRange, true, false);
    calcHist(&RGB[2], 1, 0, Mat(), hist[2], 1, &histSize, &histRange, true, false);

    normalize(hist[0], hist[0], 0, 1, NORM_MINMAX, -1, Mat());
    normalize(hist[1], hist[1], 0, 1, NORM_MINMAX, -1, Mat());
    normalize(hist[2], hist[2], 0, 1, NORM_MINMAX, -1, Mat());

    Mat histMat(400, 600, CV_8UC3, Scalar(255, 255, 255));

    for (int i = 1; i < histSize; i++)
    {
        line(histMat,
             Point(44 + i * 2, 400 - hist[0].at<float>(i - 1) * 300 - 50),
             Point(46 + i * 2, 400 - hist[0].at<float>(i) * 300 - 50),
             Scalar(0, 0, 255),
             2,
             8,
             0);
        line(histMat,
             Point(44 + i * 2, 400 - hist[1].at<float>(i - 1) * 300 - 50),
             Point(46 + i * 2, 400 - hist[1].at<float>(i) * 300 - 50),
             Scalar(0, 255, 0),
             2,
             8,
             0);
        line(histMat,
             Point(44 + i * 2, 400 - hist[2].at<float>(i - 1) * 300 - 50),
             Point(46 + i * 2, 400 - hist[2].at<float>(i) * 300 - 50),
             Scalar(255, 0, 0),
             2,
             8,
             0);
    }

    namedWindow("hist", WINDOW_NORMAL | WINDOW_KEEPRATIO);
    resizeWindow("hist", 600, 400);
    imshow("hist", histMat);
    waitKey();

    return 0;
}

到这里，opencv绘图功能就基本介绍完毕了。由于只是出于想要绘制直方图的目的而学的绘制功能，因此许多细节就都忽略了，只好等需要用到的时候再查找相关的方法了。

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值