leecode73 矩阵置零

我的思路

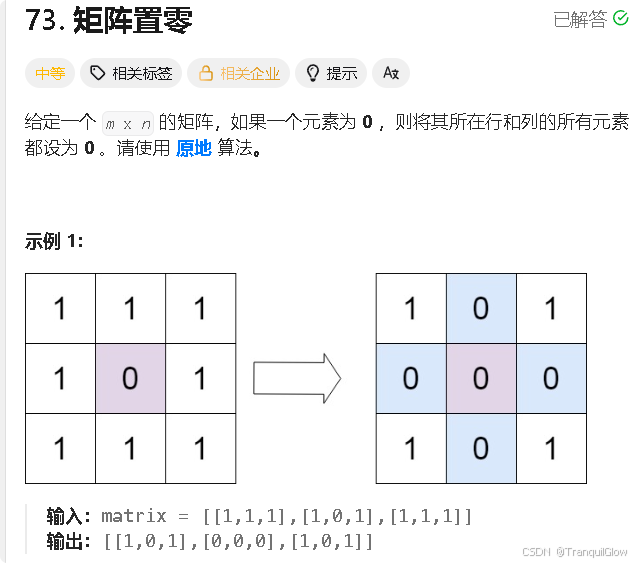
这个题目不难，就是一句话，遍历这个矩阵的时候，当遇到0的时候就把该行该列改为0，同时为了不影响后续的遍历，我们可以将这个遍历和修改分为两个数组。使用mn的辅助空间

class Solution {
   
   
    public void setZeroes(int[][] matrix) {
   
   
        //如果只是使用m+n的空间
        int m = matrix.length,n = matrix[0].length;
        Set<Integer> line = new HashSet<>();
        Set<Integer> row = new HashSet<>();
        for(int i =0;i<m;i++){
   
   
            for(int j =0;j<n;j++){
   
   
                if(matrix[i][j]==0){
   
   
                    line.add(i);
                    row.add(j);
                }
            }
        }
        for(int num:line){
   
   
            for(int k=0;k<n;k++){
   
   
                matrix[num][k]=0;
            }
        }
        for(int num:row){
   
   
            for(int k=0;k<m;k++){
   
   
                matrix[k][num]=0;
            }
        }
    }
}

如果使用m+n的辅助空间，我们可以使用set来使用，set可以去重

class Solution {
   
   
    public void setZeroes(int[][] matrix) {
   
   
        //如果只是使用m+n的空间
        int m = matrix.length,n = matrix[0].length;
        Set<Integer> line = new HashSet<>();
        Set<Integer> row = new HashSet<>();
        for(int i =0;i<m;i++){
   
   
            for(int j =0;j<n;j++){
   
   
                if(matrix[i][j]==0){
   
   
                    line.add(i);
                    row.add(j);
                }
            }
        }
        for(int num:line){
   
   
            for(int k=0;k<n;k++){
   
   
                matrix[num][k]=0;
            }
        }
        for(int num:row){
   
   
            for(int k=0;k<m;k++){
   
   
                matrix[k][num]=0;
            }
        }
    }
}

其它思路

没有找到灵神的题解，可能灵神觉得这个题目不值得研究吧。

不过找到了一个只用了O(1)复杂度的大佬，看一下他的解法

他的做法主要分为三步，利用第一行和第一列进行标记

• 第一轮：从 (1,1) 开始扫，用第一行、第一列做标记。
• 第二轮：再从 (1,1) 开始，根据标记把相应位置清零。
• 最后：根据两个 flag 决定要不要把第一行、第一列全部清零。

class Solution {
   
   
    public void setZeroes(int[][] matrix) {
   
   
        int row = matrix.length;
        int col = matrix[0].length;
        boolean row0_flag = false;
        boolean col0_flag = false;
        // 第一行是否有零
        for (int j = 0; j < col; j++) {
   
   
            if (matrix[0][j] == 0) {
   
   
                row0_flag = true;
                break;
            }
        }
        // 第一列是否有零
        for (int i = 0; i < row; i++) {
   
   
            if (matrix[i][0] == 0) {
   
   
                col0_flag = true;
                break;
            }
        }
        // 把第一行第一列作为标志位
        for (int i = 1; i < row; i++) {
   
   
            for (int j = 1; j < col; j++) {
   
   
                if (matrix[i][j] == 0) {
   
   
                    matrix[i][0] = matrix[0][j] = 0;
                }
            }
        }
        // 置0
        for (int i = 1; i < row; i++) {
   
   
            for (int j = 1; j < col; j++) {
   
   
                if (