递归：如何用三行代码找到“最终推荐人”？

本文是学习算法的笔记，《数据结构与算法之美》，极客时间的课程

有这么一个运用场景，某APP，用户A推荐了用户B，用户B又推荐了用户C。那C的最终推荐人就是A，B的最终推荐人也是A，而用户A没有最终推荐人。

在数据库表中，我们可以记录现行数据，其中actor_id表示用户id，referrer_id表示推荐人id。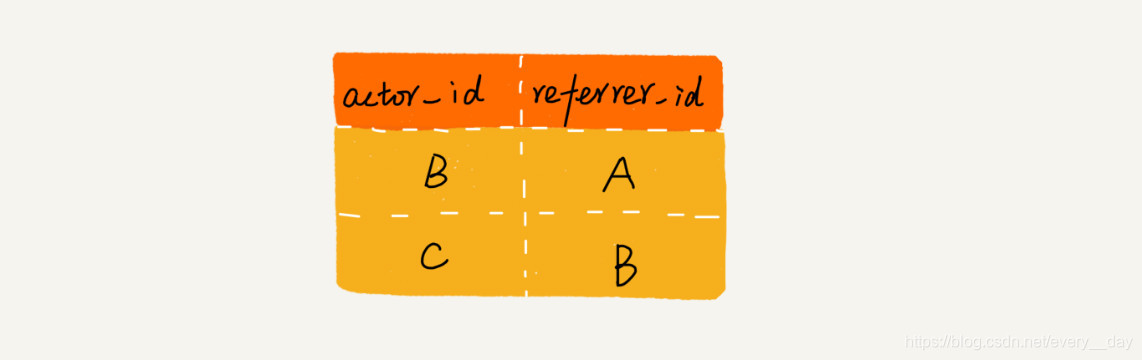
基于这个问题，给定一个用户ID，如何找出最终推荐人，带着这个问题，来学习今天的内容递归（Recursion）

如何理解递归

其实在现实生活中，我们也会遇到递归问题。比如这么一个场景，你带着女朋友到电影院看电影。女朋友问你，我们现在坐的是第几排。假设你不知道，影院又里很黑，你可以问你的前排，你的前排重复你的操作，逐一往前问，当问到第一排的时候，人家回答这是第一排，答案依次往后传，都在前一排的数字加一，最终你就可以知道自己在第几排了。翻译成代码，可以简单表示为：

f ( n ) = f ( n-1 ) + 1;  
f (1 ) = 1;

类似的这个例子的问题，可以用递归来解决。具体来讲，满足以下几个条件
1、一个问题可以拆分成几个子问题，比如你要知道自己在第几排，只需要知道前排是第几排即可
2、一个问题的解决方法子问题的解决方法，除了数据规模不一样，其它的都一样。比如前排想知道自己在第几排，只需要知道他的前排是第几排，和原问题的解决思路是一致的。
3、存在终止条件。比如第一排的不需要再问下去。也就是 f (1) = 1;

如何编写递归代码

写递归代码的关键是，写出递推公式，找出终止条件。剩下 的把递推公式转化成代码就简单多了。

咱们看一个稍微复杂的例子，这里有 n 个台阶，你每次可以走一个台阶，也可以每次走两个台阶，请问 n 个台阶有多少种走法，比如 当 n=4，时，所有的方式包括1111、22、112、121、211总共5种，这个规模我们大脑还可以想出来，试想当 n=10 时，想出来几种走法，估计有点内存不够了吧。

怎么用递归的来解决呢？ 10个台阶有多少种走法，倒推一步，到第10阶的前一步，要么在第9阶，跨一步到第10阶，要么在第8阶，跨两步到第10阶（只倒推一步！！）那么 f (10) = f(9) + f(8)。如果觉得有点饶，那看下f(4)，f(3)有3种（111，12，21）；f（2）的有两种（11，2），f(4) = f(3) + f(2)，没有重复计算，也没有遗漏。

用代码语言来说明，就是上到第4台阶的只有两种情况，一种是经过第3个台阶上到，另一种是不经过第3个台阶上到，前者对应f(3) ，后者对应 f(2)。递推公式：**f(n) = f(n-1) + f(n-2)**好了递推公式说明到这儿了。

再说终止条件，f(1) = 1，f(2) = 2。
如果只有前一条，那么f(2) = f(1) + f(0)，这个就无法计算了，甚至会出现无限循环。找终止条件时，用较小的几个数来试试，确保可以终止且不出错。也就是

f (1) = 1;
f (2) = 2;
f (n) = f (n-1) + f (n-2);

有了递推公式和终止条件，翻译成代码就容易多了

int count( n ){
	if ( n = 1){
		return 1;
	}
	if ( n = 2){
		return 2;
	}
	return f (n-1) + f (n-2);	
}

写递归代码，就是找出把大问题拆解为小问题的规律，在此基础上找出递推公式和终止条件，将此翻译为代码。不要试图用人脑去分解一层层的调用关系，咱大数的大脑不擅长做这样的事儿。

写递归代码要警惕堆栈溢出，要避免重复计算

在讲“栈”的那一节我们说过，函数调用时，会将临时变量封装为栈桢压入内存栈中，等函数执行完才出栈。当递归代码调用非常深，一直压入栈，就会有溢出的风险。简单的处理方法就是限制调用的深度。

另外一个问题，就是重复计算问题，比如上台阶的例子中，要计算 f (10)，就要计算 f (9) 和 f (8)，而计算 f (9)时，同样也要计算 f (8)，这样 f (8) 就被重复计算了许多次，为了避免这个问题，代码可以简单处理下。

int count( n ){
	
	if ( n = 1){
		return 1;
	}
	if ( n = 2){
		return 2;
	}
	if (resultMap.constansKey(n)){
		return resultMap.get(n);
	}
	int result =  f (n-1) + f (n-2);
	resultMap.put(n,result)
	return result;	
}

除了这两个问题，递归代码还会遇到很多问题，比如电影院的例子，它的空间复杂度就不是 O(1)，而是O(n)。每一次调用，它都要申请额外的空间，累积的空间复杂度也是很惊人的。

怎样把递归代码改为非递归代码

对于电影院的例子，f ( n ) = f ( n-1 ) + 1，很容易改成非递归代码的

int count(nit n){
	int result= 0;
	for(int i = 1; i <= n; i ++){
		result += 1;
	}
	return result;
}

对于台阶的例子，也可以改为非递归代码，只是比上个例子稍微复杂一点而已

int count(nit n){

    	if(n == 1) {
    		return 1;
    	}
    	if (n == 2) {
			return 2;
		}
    	int prePre = 1;
    	int pre = 2;		
    	int now = 1;
    	for(int i = 3; i <= n; i ++){
    		now = pre + prePre;
    		prePre = pre;
    		pre = now;
    	}
    	return now;
}

是不是所有的递归代码都可以改为迭代循环的的非递归写法呢？

笼统地讲，是的。因为递归的本身是借助栈来实现的，只不过我们使用的栈是系统或是虚拟机本身提供的，我们没有感知罢了。如果我们自己在内存堆上实现酷我，手动模拟入栈、出栈过程，这样任何递归代码都可以改成看上去不是递归代码的样子。

但是这种思路实际上是将递归改为了“手动”的递归，本质上并没有改变，而且也并没有解决前面讲到的某些问题，徒增实现的复杂度。

解答开篇

如何找到最终推荐人？

long findRootReferrerId( long actorId){
	Long referrerId = select referrer_id from [table] where actor_id = actorId;
	if( referrerId == null ){
		return actorId;
	}
	return findRootReferrerId( referrerId );
}

好了，递归的问题就讲完了，递归代码虽然简洁高效，但也有很多弊端，比如，堆栈溢出、重复计算，空间复杂度高等等。所以写递归代码时，一定要控制好这些副作用。