在Transformer中自注意力计算过程中,需要除以dk\sqrt{{{d}_{k}}}dk
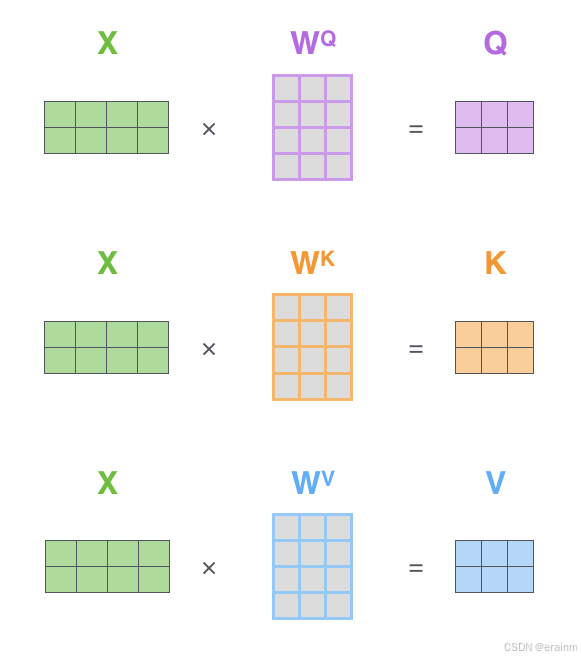
注意,上图中,WQ{W}^{Q}WQ、WK{W}^{K}WK、WV{W}^{V}WV三个参数矩阵,大小相同,数值不同~
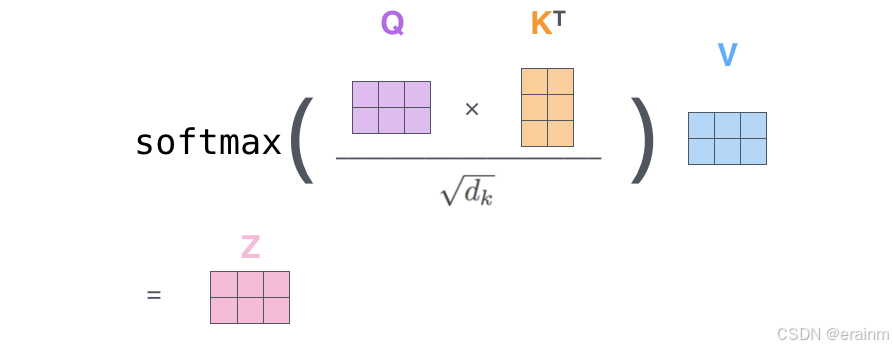
为什么需要除以dk\sqrt{{{d}_{k}}}dk?
- 缩放点积结果,避免信息损失。当超高维度向量做点积,结果可能会非常大,这样的结果经过
softmax后,可能会出现很极端的值,softmax的结果会变得非常接近n-hot向量,损失大量信息。 - 保持数值稳定性。Softmax函数的输入值如果过大,会导致数值计算上的不稳定。例如,当输入值
非常大时,指数函数的结果可能会超出浮点数的表示范围,导致溢出。通过缩放点积结果,可以避免这
种情况,确保数值计算的稳定性。 - 保持点积方差不变。假设Query和Key向量是独立同分布的随机变量,那么它们的点积结果的方差
会随着维度的增加而线性增加。为了保持点积结果的方差不变,需要除以dk\sqrt{{{d}_{k}}}dk。
证明:
# Created by erainm on 2025/12/8 15:37.
# IDE:PyCharm
# @Project: PythonProjectDemo
# @File:sqrt_dk
# @Description:
import matplotlib.pyplot as plt
import numpy as np
def showData(data): # 1 个用法
# 设置中文字体和解决负号显示问题,直接使用rcParams设置字体
plt.rcParams['font.sans-serif'] = ['PingFang SC', 'SimHei', 'Arial Unicode MS']
plt.rcParams['axes.unicode_minus'] = False
# 创建柱状图
plt.figure(figsize=(10, 6))
plt.bar(range(len(data)), data)
# 添加标题和标签
plt.title('基本柱状图示例')
plt.xlabel('数据索引')
plt.ylabel('数值')
# 显示网格
plt.grid(axis='y', alpha=0.75)
plt.show()
def generate_matrices_and_compute(m, n): # 1 个用法
"""
生成m*n矩阵和n*m矩阵,计算点积并应用softmax
"""
# 生成随机矩阵
matrix_a = np.random.rand(m, n) # m*n矩阵
matrix_b = np.random.rand(n, m) # n*m矩阵
print("矩阵 A ({}x{}):".format(m, n))
print(matrix_a)
print("\n矩阵 B ({}x{}):".format(n, m))
print(matrix_b)
# 计算点积
dot_product = np.dot(matrix_a, matrix_b)
#dot_product = np.dot(matrix_a, matrix_b)/math.sqrt(m)
# print("\n点积结果 ({{}}x{{}}):".format(m, m))
# print(dot_product)
# 应用softmax
# 对每一行应用softmax
softmax_result = np.exp(dot_product) / np.sum(np.exp(dot_product), axis=1, keepdims=True)
print("\nSoftmax结果 ({}x{}):".format(m, m))
print(softmax_result)
showData(softmax_result[0].tolist())
return matrix_a, matrix_b, dot_product, softmax_result
if __name__ == "__main__":
m, n = 3, 4 # 可以修改这些值
print("=" * 50)
print("矩阵运算示例: m={}, n={}".format(m, n))
print("=" * 50)
A, B, dot, softmax = generate_matrices_and_compute(m, n)
# 验证结果
print("\n验证:")
print("点积矩阵形状:", dot.shape)
print("Softmax矩阵形状:", softmax.shape)
print("每行之和:", np.sum(softmax, axis=1)) # 每行之和应该为1
先采用小矩阵,不除以dk\sqrt{{{d}_{k}}}dk,看一下效果:
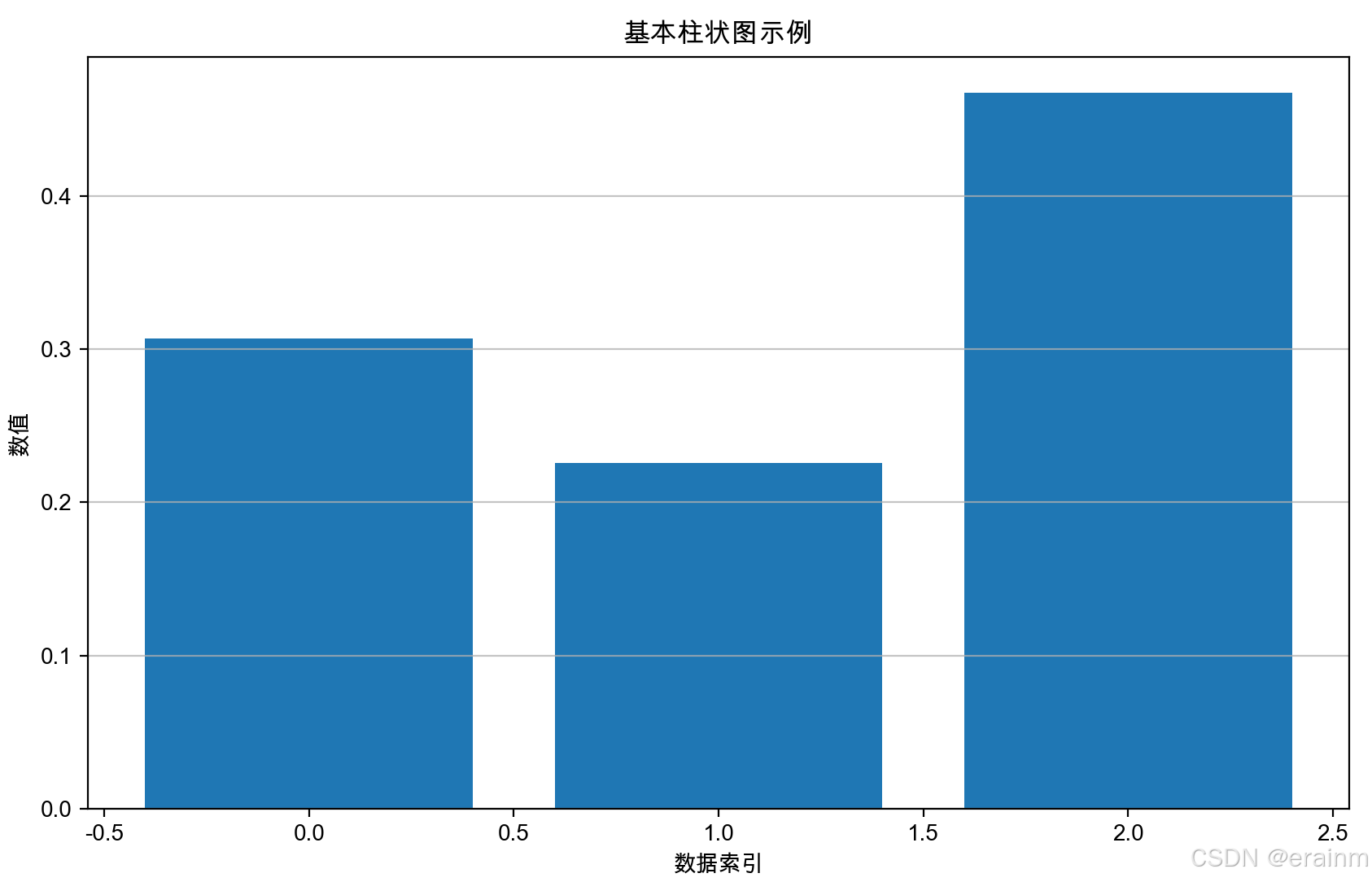
看起来效果还不是太明显,那么接着增大维度:
将m和n扩大到300,400
看下效果:
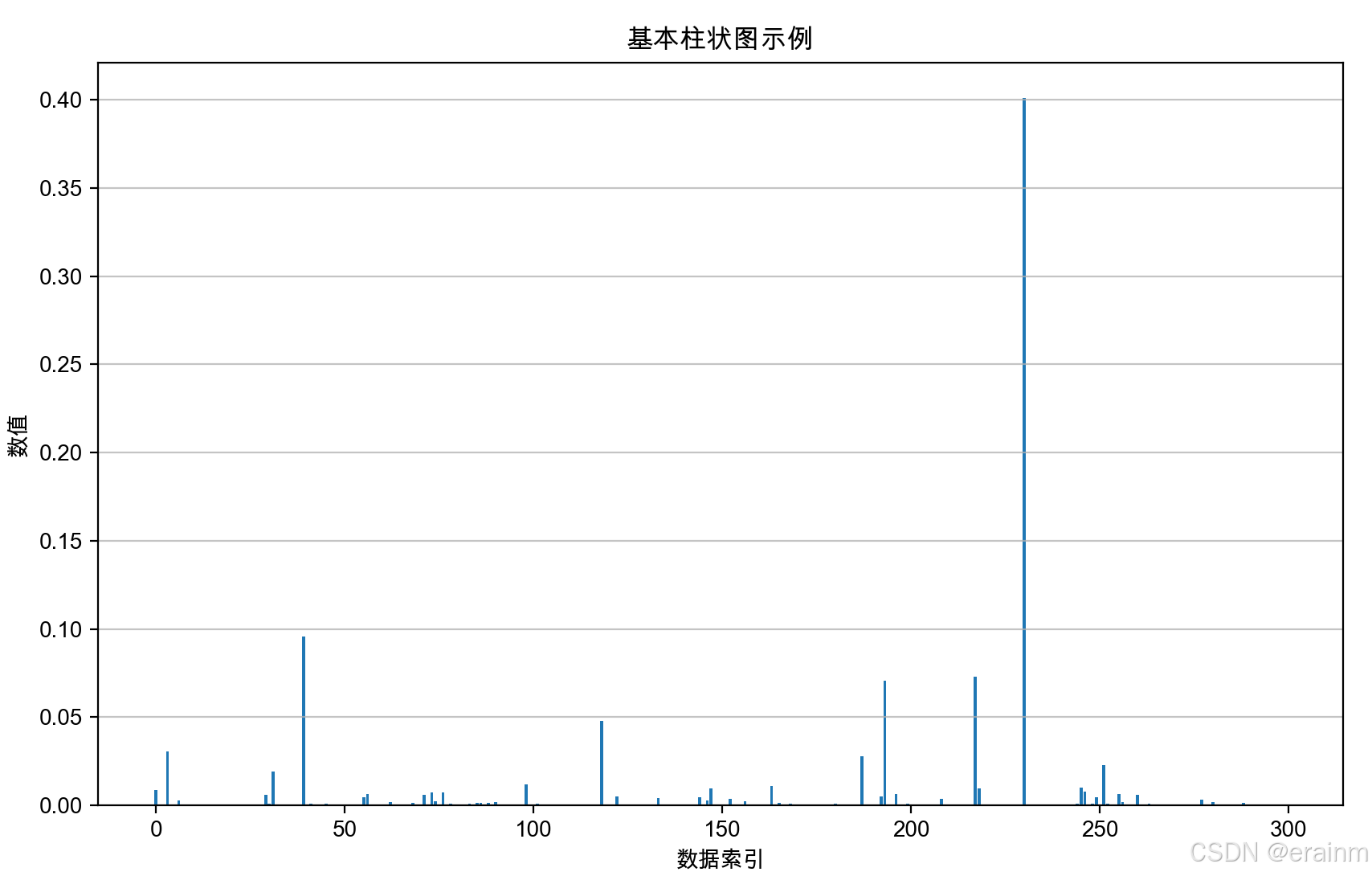
这么看来,是不是效果很明显了,当矩阵维度越大时,得到的信息会丢失掉很多。
接着采用m和n为300,400,但是除以dk\sqrt{{{d}_{k}}}dk,再看一下效果:
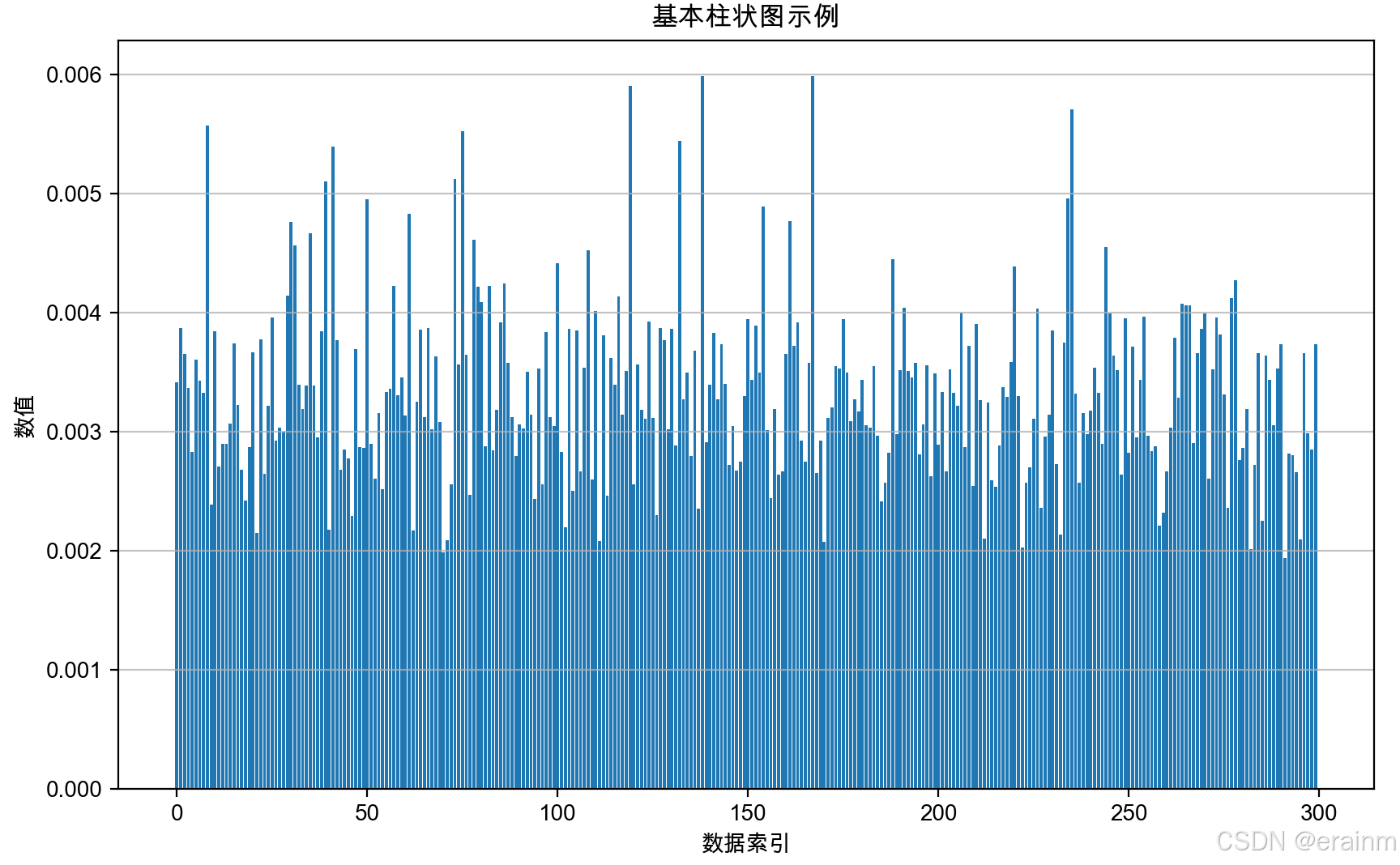
这么看来,除以dk\sqrt{{{d}_{k}}}dk,可以缩放点积结果,避免信息损失。而且保持数值稳定性。






















 179
179

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










