AI大模型基础-排序算法

原创已于 2025-07-15 19:01:53 修改 · 185 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法

于 2025-07-15 12:04:45 首次发布

零基础入门AI大模型 - 基础篇专栏收录该内容

14 篇文章 ¥59.90 ¥99.00

订阅专栏

超级会员免费看

一、排序算法 - 稳定性

1. 排序和排序算法

排序：使一串记录，按照其中的某个活某些关键字的大小递增活递减。
排序算法：使记录递增或递减的方法

2. 什么是稳定性算法？

具有相同关键字的记录通过排序后，相对位置不变，这样的算法是稳定性算法

3. 稳定性算法和不稳定性算法举例

不稳定的排序算法：选择排序、快速排序、希尔排序、堆排序
稳定的排序算法：冒泡排序、插入排序、归并排序、基数排序

二、冒泡排序

1. 什么是冒泡排序

**冒泡排序：**重复的走访要排序的元素列，依次比较相邻的两个元素，如果顺序（如从大到小、首字母从Z到A）错误，就把他们交换过来。走访元素的工作是重复的进行直到没有相邻元素需要交换，也就是说元素列已经排序完成
这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列顶端（升序或降序列），就如同碳酸饮料中的二氧化碳的气泡最终会上浮到顶端一样，故名“冒泡排序”

2. 冒泡排序实现原理

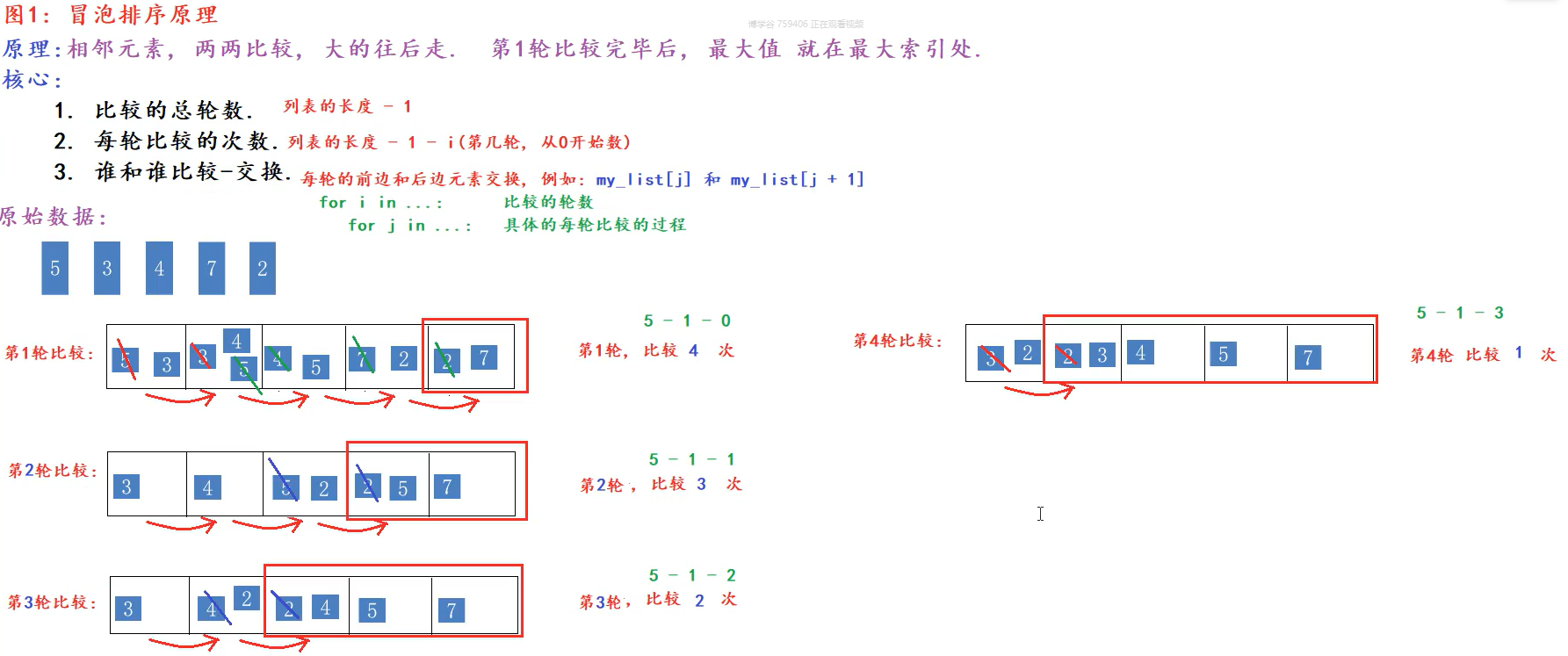
相邻元素，两两比较，大的往后走，第一轮比较完毕后，最大值就在最大索引处
核心点：
a. 比较的总轮数
b. 每轮比较的次数
c. 谁和谁比较、交换
在这里插入图片描述

时间复杂度：
最优时间复杂度：O(n)
最坏时间复杂度：O(n²)
冒泡排序属于稳定性算法

3. 冒泡排序 - 代码实现（Python）

# Created by erainm on 2025/7/1 20:52.
# @Description: TODO 冒泡排序算法

def bubble_sort(my_list):
    """
    通过冒泡排序，对元素列表进行排序
    核心：
        1. 比较的总轮数：          列表长度 - 1
        2. 每轮比较的次数:         列表的长度 - 1 - i（代表：轮数，从0开始计数
        3. 谁和谁比较：            my_list[j] = my_list[j + 1]
    :param my_list: 传入的集合
    :return: 排序后的集合
    """
    list_len = len(my_list)
    for i in range(list_len - 1):           # 外循环，控制比较的轮数
        cnt = 0                             # 使算法程序更优
        for j in range(list_len - 1 - i):   # 内循环控制比较的次数
            if my_list[j] > my_list[j + 1]:
                my_list[j], my_list[j + 1] = my_list[j + 1],my_list[j]
                cnt += 1
        if cnt == 0:
            break


if __name__ == '__main__':
    my_list = [2,4,1,6,23,685,2,54,6]
    print(f'排序前：{my_list}')
    bubble_sort(my_list)
    print(f'排序后：{my_list}')

三、选择排序

1. 什么是选择排序

选择排序工作原理：
第一次从待排序的数据元素中选出最大（最小）的一个元素，存放到序列的起始位置，然后再从剩余的未排序元素中寻找到最大（最小）元素，然后放到已排序的序列的末尾，以此类推，直到全部待排序的数据元素的个数为零。

2. 冒泡排序实现的原理

原理：
每轮比价，都找到最小值所在索引，然后和最小索引进行交换即可
**推理过程：**假设列表长度为 5
比较轮数每轮比较的次数谁（索引）和谁（索引）比较外循环（i），内循环（j）
0 4 0和1，0和2，0和3，0和4 0 1～4
1 3 1和2，1和3，1和4 1 2～4
2 2 2和3，2和4 2 3～4
3 1 3和4 3 4
时间复杂度：
最优时间复杂度：O(n)
最坏时间复杂度：O(n²)
选择排序属于不稳定排序

3. 冒泡排序 - 代码实现(Python)

# Created by erainm on 2025/7/1 21:21.
# @Description: TODO 选择排序

"""
选择排序：
    原理：
        每轮比价，都找到最小值所在索引，然后和最小索引进行交换即可
    推理过程：假设列表长度为 5
        比较轮数        每轮比较的次数     谁（索引）和谁（索引）比较       外循环（i）， 内循环（j）
           0                4           0和1，0和2，0和3，0和4           0         1～4
           1                3           1和2，1和3，1和4                 1         2～4
           2                2           2和3，2和4                      2         3～4
           3                1           3和4                           3           4
    核心：
        1. 比较总轮数：           列表长度 - 1
        2. 每轮比较次数：          i + 1 ～ 列表长度 - 1
        3. 谁和谁比价：           my_list 和 my_list[min_index]
    时间复杂度：
        最优时间复杂度：O(n)
        最坏时间复杂度：O(n²)
    选择排序属于 不稳定排序
"""
def selection_sort(my_list):
    """

    :param my_list: 要排序的列表
    :return: 排序后的列表
    """
    list_len = len(my_list)
    for i in range(list_len - 1):               #开始每轮 每次比较的次数
        min_index = i                           # 假设每轮第一个值，为最小值
        for j in  range(i+1,list_len):          # 每次比较次数
            if my_list[j] < my_list[min_index]:     # 如果当前元素 比min_index记录元素还小，就用min_index记录住该元素的索引
                min_index = j
        if min_index != i:                      # 走到这，说明第一轮比较完毕，我们要看min_index的值有无发生改变，改变了，就是找到了本轮最小值
            my_list[i],my_list[min_index] = my_list[min_index],my_list[i]

if __name__ == '__main__':
    my_list = [3,9,34,2,5,7,34,5,1,34]
    print(f'排序前：{my_list}')
    selection_sort(my_list)
    print(f'排序后：{my_list}')

四、插入排序

1. 什么是插入排序

插入排序：
插入排序的基本操作就是将一个数据插入到已经排好序的有序数据中，从而得到一个新的、个数加一的有序数据，算法适用于少量数据的排序。
插入排序的组成：
插入算法吧要排序的数组分成两部分：第一部分是有序的数字（这里可以默认数组第一个数字为有序的第一部分），第二部分为无序的数字（这里除了第一个数字以外剩余的数字可以认为是无序的第二部分）

2. 插入排序实现原理

原理：
把列表分为两部分，即：前面的是有序列表，后边的是无序列表，然后拿着无序列表的每个元素插入到有序列表的合适位置即可。
推理过程：
比较的轮数每轮比较的次数谁（索引）和谁比（索引）外循环（i）内循环（j）
1 1 1 和 0 1 1~0
2 2 2和0、2和1 2 2~0
3 2 3和2，3和1，3和0 3 3~0
4 1 4和3，4和2，4和1，4和0 4 4~0
时间复杂度：
最优时间复杂度：O(n)
最坏时间复杂度：O(n²)
冒泡排序属稳定性算法

3. 插入排序 - 代码实现（Python）

#!/usr/bin/env python
# -*- coding: UTF-8 -*-
'''
@Project     ：python_project
@File        ：insertion_sort.py
@Create at   ：2025/7/2 10:02
@version     ：V1.0
@Author      ：erainm
@Description : 插入排序
原理：
    把列表分为两部分，即：前面的是有序列表，后边的是无序列表，然后拿着无序列表的每个元素插入到有序列表的合适位置即可。
推理过程：
    比较的轮数       每轮比较的次数         谁（索引）和谁比（索引）            外循环（i）      内循环（j）
        1                1                    1 和  0                      1             1~0
        2                2                    2和0、2和1                    2             2~0
        3                2                    3和2，3和1，3和0               3            3~0
        4                1                    4和3，4和2，4和1，4和0          4            4~0

核心：
    1. 比较的轮数： 列表长度 - 1
    2. 每轮比较的次数： i ~ 0
    3. 谁和谁比， my_list[j] 和my_list[j - 1]
'''

def insertion_sort(my_list):
    lst_len = len(my_list)
    for i in range(1, lst_len):
        for j in range(i, 0, -1):
            if my_list[j] < my_list[j - 1]:
                my_list[j], my_list[j - 1] = my_list[j - 1], my_list[j]
            else:
                break

if __name__ == '__main__':
    my_list = [23, 54, 64, 13, 4, 45, 457, 78]
    print(f"排序前：{my_list}")
    insertion_sort(my_list)
    print(f"排序后：{my_list}")

五、快速排序

1. 原理

原理：找分界值，把小于分界值的数据放到分界值的左边，大于分界值的放到分界值的右边，
即：小分界值大（这种格式）
通过递归的思路，对于分界值两边的数据，分别可以进行排序
在这里插入图片描述

时间复杂度：
最差时间复杂度和最优时间复杂度：
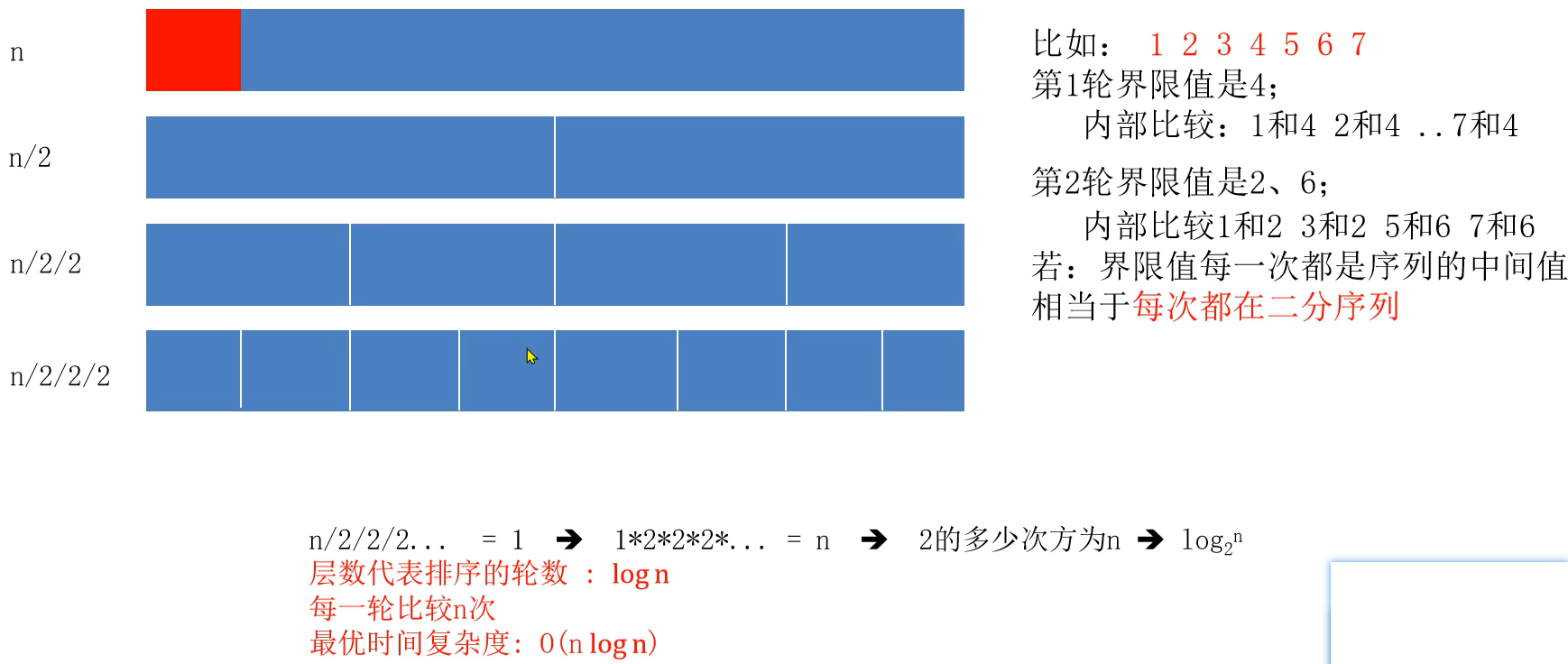
在这里插入图片描述

2. 快速排序 - 代码实现（Python）

#!/usr/bin/env python
# -*- coding: UTF-8 -*-
'''
@Project     ：python_project
@File        ：quick_sort.py
@Create at   ：2025/7/2 17:47
@version     ：V1.0
@Author      ：erainm
@Description : 快速排序

原理：
    1. 假设列表的第一个值为分界值，然后将 所有小于分界值的数据，放到分界值左边，将所有大于分界值的数据，放到分界值右边
    2. 此时我们得到列表：小、分界值、大，第二轮我们又可以从这个列表中，左右双方再次找出两个分界值，重复上述步骤
    3. 重复上述步骤，直至所有的数据，全部排列成功，左右双方可以各自独立相互排序
'''

def quick_sort(lst,start,end):
    if start >= end:
        return          # 结束递归，排序完成
    # 定义变量left 和 right 表示起始和结束索引
    left = start
    right = end
    # 定义变量middle(mid)表示分界值，假设列表的第一个元素为：分界值
    mid = lst[start]
    # 具体查找（排序）的过程,只要left<right, 就说明没找完，就一直找
    while left < right:
        # 把分界值右边 比 分界值小的数据 放到分界值左边
        # 如果right位置的值比分界值大 ，right-=1
        while lst[right] > mid and left < right:
            right -= 1
        # 走到这，说明，right索引的值比分界值小，赋值即可
        lst[left] = lst[right]
        # 把分界值左边 比分界值大的数据 放大分界值右边
        # 如果left位置的值 比 分界值小，left += 1
        while lst[left] < mid and left < right:
            left += 1
        # 走到这，说明，left索引的值比分界值大，赋值即可
        lst[right] = lst[left]
    # left >= right,即left索引的位置就是分界值的位置
    lst[left] = mid

    # 循环完成后，递归继续往下继续，分别对分界值左边和右边的数据进行重复操作
    # 分界值左边数据继续排序
    quick_sort(lst,start,left-1)
    # 分界值右边数据继续排序
    quick_sort(lst,right+1,end)

if __name__ == '__main__':
    lst = [3,2,6,1,8,56,9]
    quick_sort(lst,0,len(lst)-1)
    print(lst)

六、二分查找

二分查找又称折半查找，它是一种效率较高的查找方法

1. 原理

**原理：**将数组分为三部分，一次是中值前、中值、中值后
将要查找的值与中值进行比较，若小于中值则在中值前面找，若大于中值则在中值后面找，等于中值时直接返回。

2. 二分查找过程

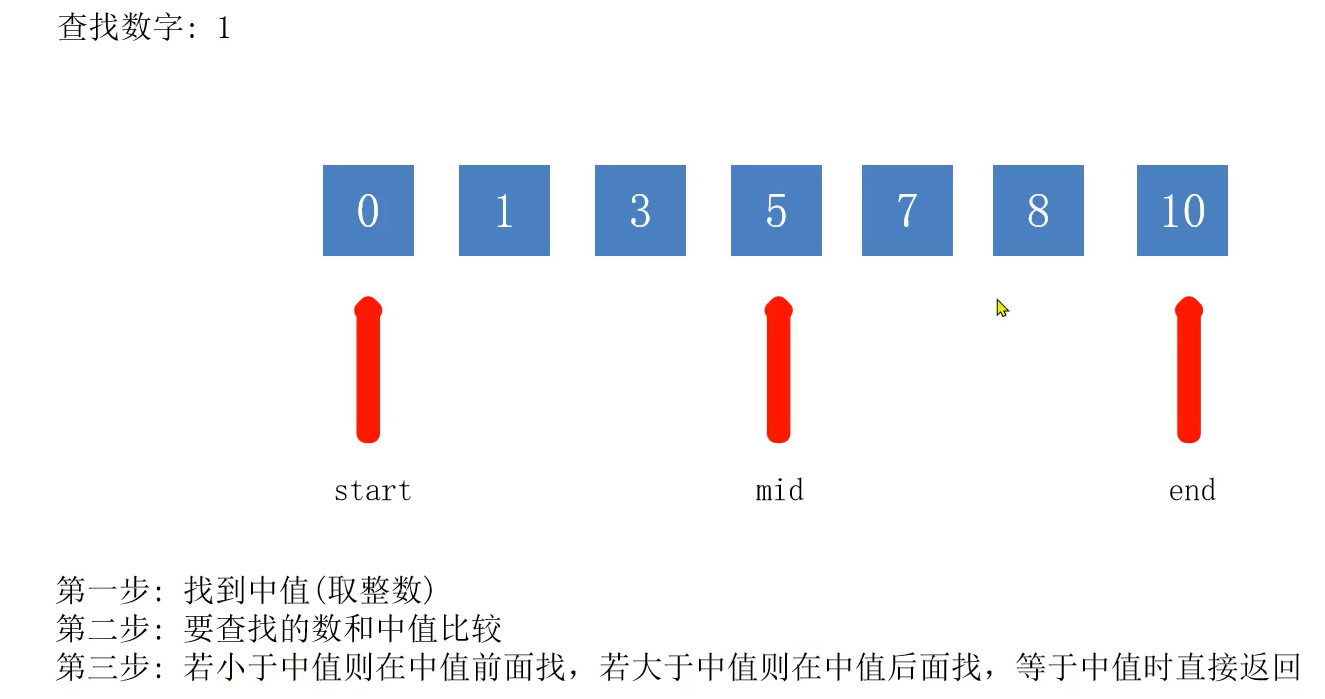
在这里插入图片描述

二分查找要求：
① 必须采用顺序存储结构
② 必须按关键字大小有序排列
时间复杂度：
最优时间复杂度：O(1)
最坏时间复杂度：O(log n)
选择排序属于不稳定排序

3. 二分查找 - 代码实现(递归版)（Python）

#!/usr/bin/env python
# -*- coding: UTF-8 -*-
'''
@Project     ：python_project
@File        ：binary_search_recursion.py
@Create at   ：2025/7/2 10:34
@version     ：V1.0
@Author      ：erainm
@Description : 二分查找（递归版）
    前提：
        要查找的列表必须是有序的
    原理：
        找到中间值，如果要查找的值 和 中间值一致，返回ture
        如果比中间值小，就去中前值（中间值左边） 查找
        如果比中间值大，就去中后值（中间值右边） 查找
'''
def binary_search_recursion(lst, target):
    # 获取列表长度
    lst_len = len(lst)
    # 判断列表长度为0，返回false
    if lst_len == 0:
        return False
    # 获取列表中间值索引
    mid = lst_len // 2
    # 比较
    if lst[mid] == target:
        return True
    elif lst[mid] < target:
        return binary_search_recursion(lst[mid + 1 :], target)
    else:
        return binary_search_recursion(lst[:mid], target)

if __name__ == '__main__':
    lst = [1,3,5,7,9,11,13,15,17,19]
    print(binary_search_recursion(lst, 19))

4. 二分查找 - 代码实现（非递归版）（Python）

#!/usr/bin/env python
# -*- coding: UTF-8 -*-
'''
@Project     ：python_project
@File        ：binary_search.py
@Create at   ：2025/7/2 10:59
@version     ：V1.0
@Author      ：erainm
@Description : 二分查找（非递归）
'''
def binary_search(lst, target):
    lst_len = len(lst)
    start = 0
    end = lst_len - 1
    while start <= end:
        mid = (start + end) // 2
        if target == lst[mid]:
            return True
        elif target < lst[mid]:
            end = mid - 1
        else:
            start = mid + 1
    return False


if __name__ == '__main__':
    lst = [1,3,5,7,9,11,13,15,17,19]
    print(binary_search(lst, 3))