62.不同路径

思路
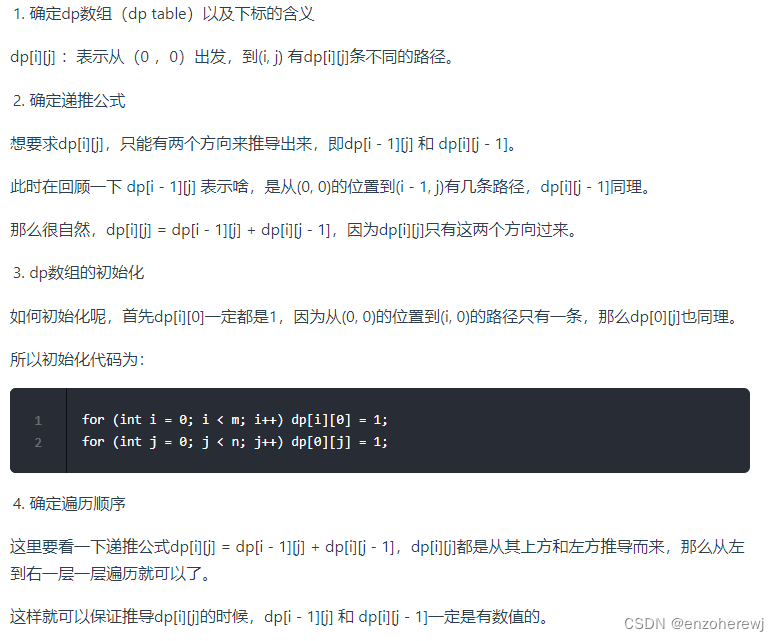

代码
用二维dp
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
dp = [[0] * n for _ in range(m)]
for i in range(m):
dp[i][0] = 1
for i in range(n):
dp[0][i] = 1
for i in range(1, m):
for j in range(1, n):
dp[i][j] = dp[i-1][j] + dp[i][j-1]
return dp[-1][-1]
- 时间复杂度:
O(m × n) - 空间复杂度:
O(m × n)
一维dp优化
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
dp = [1] * n
for _ in range(m-1):
for i in range(1, n):
dp[i] += dp[i-1]
return dp[-1]
- 时间复杂度:
O(m × n) - 空间复杂度:
O(n)
63. 不同路径 II

思路
本题的思路和上一题相似。dp的转移方程和遍历顺序是一样的,但是赋值和初始化有些不同。
不同的地方在于有了障碍物,需要对此作出一些调整。
在初始化的时候,dp[i][j]为0。在给第一行第一列赋
1的初始值时,只要遇到障碍物即可停止赋值了,因为过不去。
在给dp[i][j]赋值的时候,如果遇到障碍物就跳过
代码
class Solution:
def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
m = len(obstacleGrid)
n = len(obstacleGrid[0])
dp = [[0] * n for _ in range(m)] # 初始化
# 给第一列赋 1的值
for i in range(m):
if obstacleGrid[i][0] == 1:
break
else:
dp[i][0] = 1
# 给第一行赋 1的值
for i in range(n):
if obstacleGrid[0][i] == 1:
break
else:
dp[0][i] = 1
# 给dp数组赋值
for i in range(1, m):
for j in range(1, n):
if obstacleGrid[i][j] == 1:
dp[i][j] = 0 # continue也可以
else:
dp[i][j] = dp[i-1][j] + dp[i][j-1]
return dp[-1][-1]
- 时间复杂度:
O(m × n) - 空间复杂度:
O(m × n)
同样,本题也可以对dp数组进行优化,实际上一个一维的dp数组即可满足要求。

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








