6.1树的定义、基本术语

• 前面介绍的都是线性结构（顺序表、链表、串、队列、数组、广义表…），下面开始介绍树形结构。

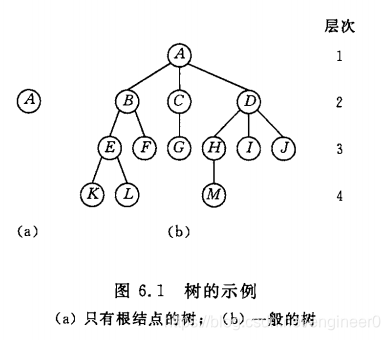
• 根：任意一颗非空树中有且仅有一个根（结点），如 (a) 中的 A ，(b) 中的 A
  子树：(b) 中 T₁ = {B, E, F, K, L }，T₂ = {C, G}，T₃ = {D, H, I, J, M}。T₁，T₂ 和T₃ 本身又是树，称为根 A 的子树。以此类推，{E, K, L } 和 F 是 B 的子树。就算是一个结点也可以是子树。
  结点：包含一个数据元素和若干指向其子树的分支。
  结点的度：一个结点拥有的子树数量。
  树的度：树中所有结点中度的最大值。
  叶子结点 / 终端节点：度为 0 的结点。
  分支结点 / 非终端节点 / 内部结点：度不为 0 的结点。
  孩子 / 孩子结点：一个结点的子树的根结点称为该结点的孩子。
  双亲 / 双亲结点：一个结点是他的孩子结点的双亲结点。
  兄弟 / 兄弟结点：具有相同双亲的结点互为兄弟结点。
  祖先 / 祖先结点：从根结点到该结点所路过的所有分支上的结点，如 M 的祖先为 A, D, H。
  子孙 / 子孙结点：以某一结点为根的子树中，这个根下面的所有结点都是这个根的子孙。如 B 的子孙为 E, K, L, F。
  层次：从根开始计数，根在第一层，根的孩子在第二层，…直到终端结点，每个结点都有对应的层次。
  堂兄弟：双亲不同但在同一层次的结点互为堂兄弟。
  树的深度 / 高度：树中结点的最大层次数。
  有序树 / 无序树：树中各结点的各子树从左到右是有次序的，不能互换，则为有序树。否则是无序树。
  森林：m（m>=0）棵不相交的树的集合。对于树中的每一个结点，其子树的集合就是森林。

• 树、森林的递归定义
  任何一颗树都可以看作是一个二元组：Tree = ( root, F )
  root：根节点
  F：root 的 m（m>=0）棵子树的集合，也是森林。F = （T₁, T₂, … ,T_m）。其中 T_i = (r_i, F_i) 又称为 root 的第 i 棵子树。

• 树的相似
  两棵二叉树要么都是空，要么都不空，并且它们的各级的左右子树均是如此，那么称这两棵二叉树是相似的。

// 递归比较两棵二叉树是否相似，分别遍历两棵二叉树
Status SimilarTree(BiTree &T1, BiTree &T2)
{
	if(!T1)
	{
		// T1是空树
		if(!T2)
		{
			// T2也是空树
			return TRUE;
		}
		else
		{
			return FALSE;
		}
	}
	else
	{
		// T1是非空树
		if(!T2)
		{
			// T2也是非空树
			if(SimilarTree(T1->rchild, T2->lchild) 
					&& SimilarTree(T1->rchild, T2->rchild) )
			{
				return TRUE;
			}
			else
			{
				return FALSE;
			}
		}
	}
}