6.2 二叉树

二叉树的定义和性质

• 二叉树的定义：
  二叉树也是树形结构，但是它的每个结点至多有两颗子树（度最大为2）。并且是有序的，子树有左右之分。
  二叉树一定是有序树，而其他的树未必是有序的，度为2的树未必是有序树。

• 二叉树的五种基本形态：空，无左右子树，只有左子树，有左右子树，只有右子树。
  

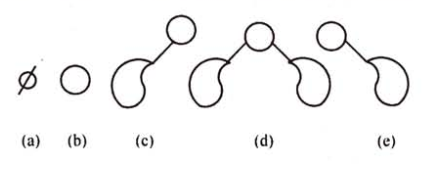
• 满二叉树
  一颗深度为 k 且有 2^k - 1 个结点的二叉树称为满二叉树。
  满二叉树每一层上的结点数都是最大结点数。

• 完全二叉树
  深度为 k ，有 n 个结点的二叉树，当且仅当其每一个结点都与深度为 k 的满二叉树中编号从1至n的结点一一对应时，称之为完全二叉树。

• 二叉树的性质
  1、二叉树的第i层上至多有 2ⁱ 个结点
  2、深度为 k 的二叉树至多有 2^k - 1 个结点
  3、在一个二叉树 T 中，总的结点数目为 n ，终端结点数目为 n₀ ，度为1的结点数目为 n₁ ，度为2的结点数目为 n₂ 。
  一一一 n = n₀ + n₁ + n₂
  一一一 n = n₁ + 2 n₂ + 1
  一一一 n₀ = n₂ + 1
  4、具有 n 个结点的完全二叉树的深度为 [ log₂ n ] + 1
  一一一 假设这个完全二叉树的深度为 k ，
  一一一 那么必然存在， 2^k-1 -1 < n <= 2^k - 1 或者 2^k-1 <= n <2^k
  一一一 那么，k - 1 <= log₂ n < k
  一一一 因为 k 是整数，因此 k = [ log₂ n ] + 1
  5、具有 n 个结点的完全二叉树（深度为 [ log₂ n ] + 1 ）的结点按层序编号（从上到下，从左到右），对于任一结点 i
  一一一 若 i == 1，则结点 i 是二叉树的根，无双亲。
  一一一 若 i > 1，则它的双亲结点是 [ i / 2 ]
  一一一 若 2 * i > n ，则结点 i 无左孩子（叶子结点）。否则它的左孩子标号为 2 * i
  一一一 若 2 * i + 1 > n，则结点 i 无右孩子。否则它的右孩子标号为 2 * i + 1
  6、具有 n 个结点的二叉树，最多有n + 1个空链域。

二叉树的存储结构

• 顺序存储结构
  用一组地址连续的存储单元自上而下，自左至右存储完全二叉树上的结点元素，编号为 i 的元素存放在下标为 i - 1 的一维数组中。
  顺序结构适用于满二叉树，完全二叉树。
  若一般二叉树也用顺序结构来存储，有 k 层二叉树，每层只有一个结点，也需要长度为 2^k - 1 的顺序表来存储；会造成存储空间浪费。

// 定义二叉树的最大结点数
#define MAX_TREE_SIZE  100
// 0号单元存储根节点	
typedef TElemType SqBiTree[MAX_TREE_SIZE];
SqBiTree bt;

• 链式存储结构 （二叉链表）
  已知二叉树的结点由一个数据域和分别指向其左右子树的两个分支域构成。
  如下图( a )
  因此二叉链表的结点至少包含三个域：数据域，左指针域，右指针域。这种链表叫做二叉链表。如下图( b )
  有时为了便于找到结点的双亲，可以在结点结构中增加一个指向双亲结点的指针域，此为三叉链表。如下图( c )
  

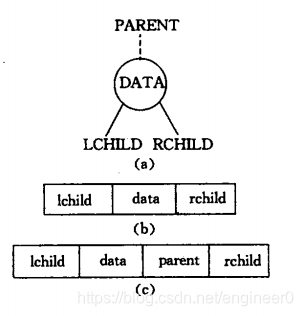
二叉链表 结点结构代码 和 图示

• 二叉链表结点结构

typedef struct BiTNode
{
	TElemType data;
	struct BiTNode *lchild, *rchild;
} BiTNode, *BiTree

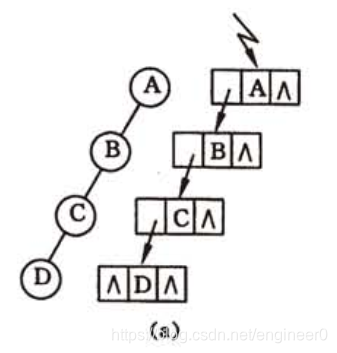
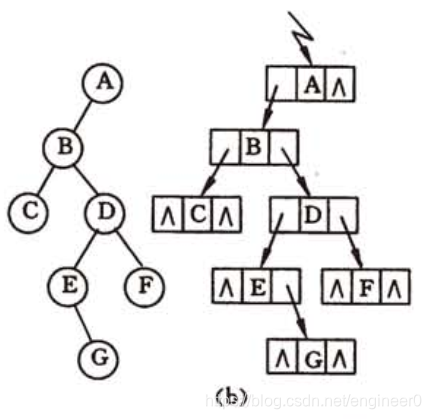
三叉链表 结点结构代码 和 图示

• 三叉链表结点结构

typedef struct TriTNode
{
	TElemType data;
	struct TriTNode *lchild, *rchild, *parent; // 比上面多了一个parent指针域
} TriTNode, *TriTree

• 三叉链表存储结构图示
  

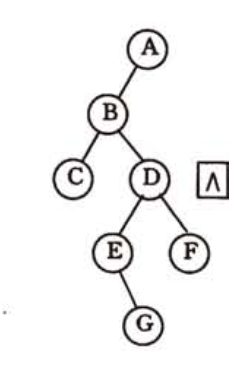
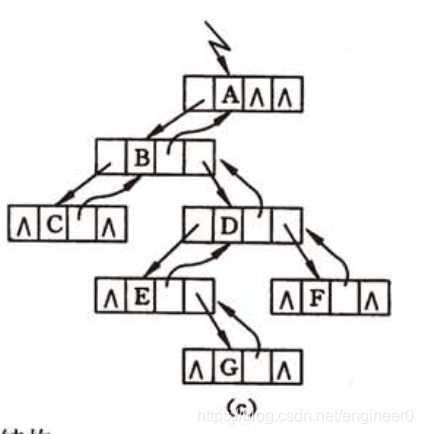
• 当需要寻找一个结点的双亲时，
  在二叉链表中需要从根指针开始遍历，
  在三叉链表中很容易实现。